湖北省湖北大学附属中学2020届高中物理 第三节匀变速直线运动的位移与时间的关系 7页

第三节匀变速直线运动的位移与时间的关系 三维目标 知识与技能 1. 知道匀速直线运动的位移与时间的关系。 2. 了解位移公式的推导方法，掌握位移公式 x=v0+(1/2)at2。 3. 理解匀变速直线运动位移与时间的关系及其应用。 4. 理解 v-t 图象中图线与 t 轴所夹的面积表示物体在这段时间内运动的位移。 5. 能推导并掌握位移与速度的关系式 v2-v02=2ax。 6. 会适当地选用公式对匀变速直线运动的问题进行简单的分析和计算。 过程与方法 1. 通过近似推导位移公式的过程，体验微元法的特点和技巧，能把瞬时速度的 求法与此比较。 2. 感悟一些数学方法的应用特点。 情感态度与价值观 1. 经历微元法推倒位移公式和公式法推导速度位移关系，培养自己动手的能力， 增加物理情感。 2. 体验成功的快乐和方法的意义，增强科学能力的价值观。 教学重点 1. 理解匀变速直线运动的位移与时间的关系 x=v0+(1/2)at2。 2. 理解匀变速直线运动的位移与速度的关系 v2-v02=2ax 及其应用。 教学难点 1. v-t 图象中图线与 t 轴所夹的面积表示物体在这段时间内运动的位移。 2. 微元法推导位移时间关系式。 3. 匀变速直线运动的位移与时间的关系 x=v0+(1/2)at2 及其灵活应用。 教具 课时安排 2 课时 教学过程 [引入]前面我们学习了匀变速直线运动速度随时间的变化规律，对于运动的问题， 人们不仅关注物体的速度随时间的变化规律，而且还希望知道物体运动的位移随时 间的变化规律。这节课就来研究物体做匀变速直线运动位移随时间的变化规律。 [板书]一、匀速直线运动的位移 [分析]我们先从最简单的一种运动方式入手分析，我们取初始时刻质点所在的位置 为坐标原点，则有 t 时刻原点的位置坐标 x 与质点在 0~t 一段时间间隔内的位移相 同。得出位移公式 x=vt。现在，大家根据速度—时间图象的意义，画出匀速直线运 动的速度—时间图象。  大家观察所画的图象，列式子求出图中矩形的面积。（可以看到，矩形的面 积正好是 vt）  当速度值正好是正值或负值，它们的位移有什么不同？（当速度为正值时， x=vt>0，图线与时间轴所围成的矩形在时间轴的上方，表示位移方向与规定 的正方向相同；当速度为负值时，x=v<0，图线与时间轴所围成的矩形在时 间轴的下方，表示位移方向与规定的正方向相反；） 那么，对于匀变速直线运动，它的位移与 v-t 图象，是不是也有类似的关系呢？我 们下面一起来分析。 [思考与讨论]下面是一位同学所做的“探究小车的运动规律”的测量记录，我们知 道小车在做匀变速直线运动，表中得到了物体在 0、1、2……，5 几个位置的瞬时速 度，原始纸带没有保存，你能不能通过表中的数据估算小车从位置 0 到位置 5 的位 移？ 位置编号 0 1 2 3 4 5 时间 t/s 0 0.1 0.2 0.3 0.4 0.5 速 度 v/(m·s-1) 0.38 0.63 0.88 1.11 1.38 1.62 [ 分 析 ] 可 以 用 下 面 的 方 法 估 算 x=0.38 × 0.1+0.63 × 0.1+0.88 × 0.1+1.11 × 0.1=……,用这样的方法进行计算，会带来一定的误差，因为，小车的速度在不断的 增加，表格中的速度只是某一个时刻的瞬时速度。 要提高估算的精确度，我们可以在当初实验记数据时减小时间间隔，当时间间 隔取得越小，精确度就越高。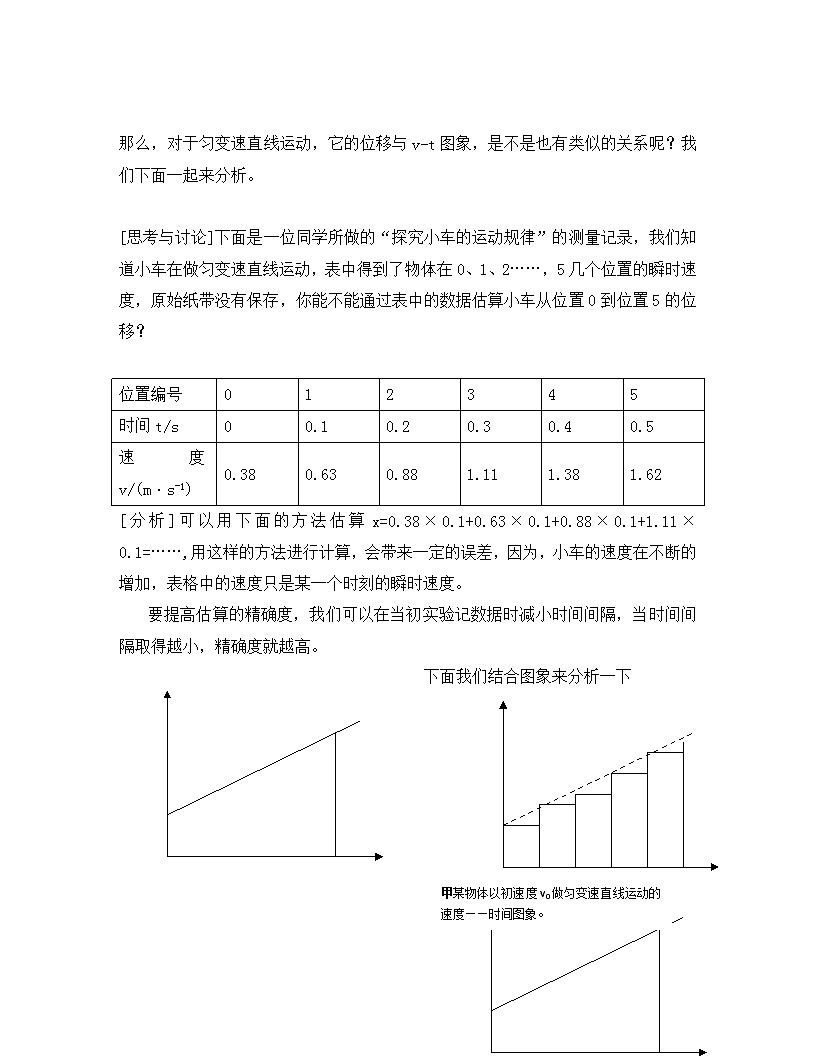 下面我们结合图象来分析一下 甲某物体以初速度 v0 做匀变速直线运动的 速度——时间图象。 由上面的分析过程，我们知道实际上，v-t 图象下面的梯形 OABC 的面积，就等于做 匀变速直线运动的物体在 0（此时的速度是 v0）到 t（此时速度是 v）这段时间的位 移。 图中梯形 OABC 的面积是 S=（1/2）（OC+AB）×OA 把面积及各条线段换成所代表的物理量，上式变为 x=(1/2)(v0+v)t 又 v=v0+at,得到 x=v0t+(1/2)at2 乙每两个位置间的位移，正好等于以 （1/5）t 为底、以速度为高的细高矩形 的面积。矩形面积之和，可以粗略地表 示整个运动过程的位移。 丙如果各位置的时间间隔小一些，这些矩形面 积之和就能比较精确地代表整个运动的位移。 丁如果时间分得非常细，小矩形就会非常多，它 们的面积就等于 CB 斜线下的面积而十分准确地 代表整个运动的位移。 这就是表示匀变速直线运动的位移与时间关系的公式。 [思考]这个公式是否使用于匀减速直线运动？ [强调]应用公式时注意，公式中除了时间 t 外，其它的物理量都是矢量，物体做直 线运动时，矢量的方向性可以在选定正方向后，用正、负来体现。一般我们都选物 体运动方向或是初速度的方向为正，在匀减速运动中，如刹车问题中，尤其要注意 加速度的方向与运动方向相反。 [做一做] 教材 P42 分析：匀变速直线运动的 x-t 图象如右图所示（二次函数 图象的一部分），图象是一条曲线，位移图象反映的是位移随时 间的变化规律，可以根据物体在不同时刻的位移在 x-t 坐标 系中描点作出。直线运动是根据运动轨迹来命名的。而 x-t 图象中的图线不是运动轨迹，因此 x-t 图象中图线是不是直线与直线运动的轨迹没 有任何直接关系。 [例题]一辆汽车以 1m/s2 的加速度加速行驶了 12s，驶过了 180m。汽车开始加速时 的速度是多少？ 分析我们研究的是汽车从开始加速到驶过 180m 这个过程。由题意可以知道，物体做匀加速直 线运动，所以可以用匀加速直线运动的规律。 解：由 x=v0t+(1/2)at2 得 v0=(x/t)-(1/2)at=(180m/12s)-(1/2)×1m/s2×12s=9m/s 汽车开始加速时的速度是 9m/s。 强调一般应该先用字母代表物理量进行运算，得出用已知量表示未知量的关系 式，然后再把数值代入式中，求出未知量的值。这样做能够清楚地看出未知量与已 知量的关系，计算也比较简便。 [课堂练习] [板书]二、匀变速直线运动的位移与速度的关系 分析：上半节我们分析了匀变速直线运动位移和时间的关系。实际上，我们还 经常要用到物体的位移与速度的关系。我们来看下面的问题 问题射击时，火药在枪筒中燃烧。燃气膨胀，推动弹头加速运动。我们把子弹 在枪筒中的运动看做匀加速直线运动，假设子弹的加速度是 a=5×105m/s2，，枪筒长 x=0.64m，请计算射出枪口时的速度。 分析一般思路：根据 x=(1/2)at2 先求出运动的时间 t，然后根据 v=at 求出子弹 离开枪口的速度 v。 我们会注意到，这个问题中，已知条件和所求的结果都不设计时间 t，它只是一 个中间量。所以，我们在更一般的规律式 v=v0+at 和 x=v0t+(1/2)at2 中，消去 t,就 得到了位移与速度的直接关系式 v2-v02=2ax 这样，上述问题就可以通过这个式子直接解出。 如果问题的已知量和未知量都不涉及时间，则用上面的式子，往往会使问题变得简 单、方便。 [小结]通过本节课的学习，同学们应该掌握匀变速直线运动的两个基本公式： x=v0t+(1/2)at2 v2-v02=2ax 在理解公式时，一定要注意结合速度——时间图象，掌握速度——时间图象中“面 积”的意义，在利用公式求解时，一定要注意公式的矢量性问题。在一般的情况下， 以初速度方向为正方向；当 a 与 v0 方向相同时，a 为正值，公式即反映了匀加速直 线运动的速度和位移随时间的变化规律；当 a 与 v0 方向相反，a 为负值，公式反映 了匀减速直线运动的速度和位移随时间的变化规律。代入公式求解时，与正方向相 同的物理量代入正值，与正方向相反的物理量应代入负值。 板书设计 一、匀速直线运动的位移 x=v0t+(1/2)at2 二、匀变速直线运动的位移与速度的关系 v2-v02=2ax 作业 P44 （2）（4） 教学心得