高中物理竞赛决赛模拟试题(有答案) 15页

- 1 - 高中物理竞赛模拟试题（决赛） 一、在一边长为 a 的正 n 边形的个顶点上，各有一个质点。从 t=0 时刻开始，各质点以相同的 速率 ν开始运动， 运动过程中所有的质点都为逆时针方向， 并且始终对准它的下一个质点运动， 问经过多少时间后所有质点同时相遇？ 二、如图所示，物体 A 质量为 m，吊索拖着 A 沿光滑竖直杆上升，吊索通过滑轮 B 与卷扬机 相连， 收吊索的速度为 ν0，滑轮 B 到竖直杆的距离为 0l ，B 滑轮在水平杆上向右以速度 ν运动。 求左边吊索恰好竖直， AB 绳与水平方向成 θ角时，吊索中的张力是多少？ 三、一个空心半圆形圆管竖直在铅垂面内，管口连线在水平面内。管内装满重量为 W 的一系 列小球，左、右最高的一个小球恰好和管口平面相切，共有 2n 个小球。求从左边起第 k 个和 第 k+1 个小球之间的相互压力（忽略所有摩擦） 四、如图所示， O、A、B 三点在同一水平直线面上， O 点有一个固定的水平长钉， A 点为一固 定点， OA 相距 l 。B 处有一小球，用一根长 2l 的轻绳和 A 点相连。现给 B 球一个竖直向下的 速度 ν0，使它要能击中 A 点。求 ν0 的最小值为多少？ 五、 质量为 M 的宇航站和和质量为 m 的飞船对接在一起沿半径为 nR 的圆形轨道绕地球运动， 这里的 n=1.25 ，R为地球半径， 然后飞传从宇航站沿运动方向发射出去， 并沿某椭圆轨道飞行， 其最远点到地心的距离为 8nR，如果希望飞船绕地球运动一周后恰好与宇航站相遇， 则质量比 m/M 应该为多少？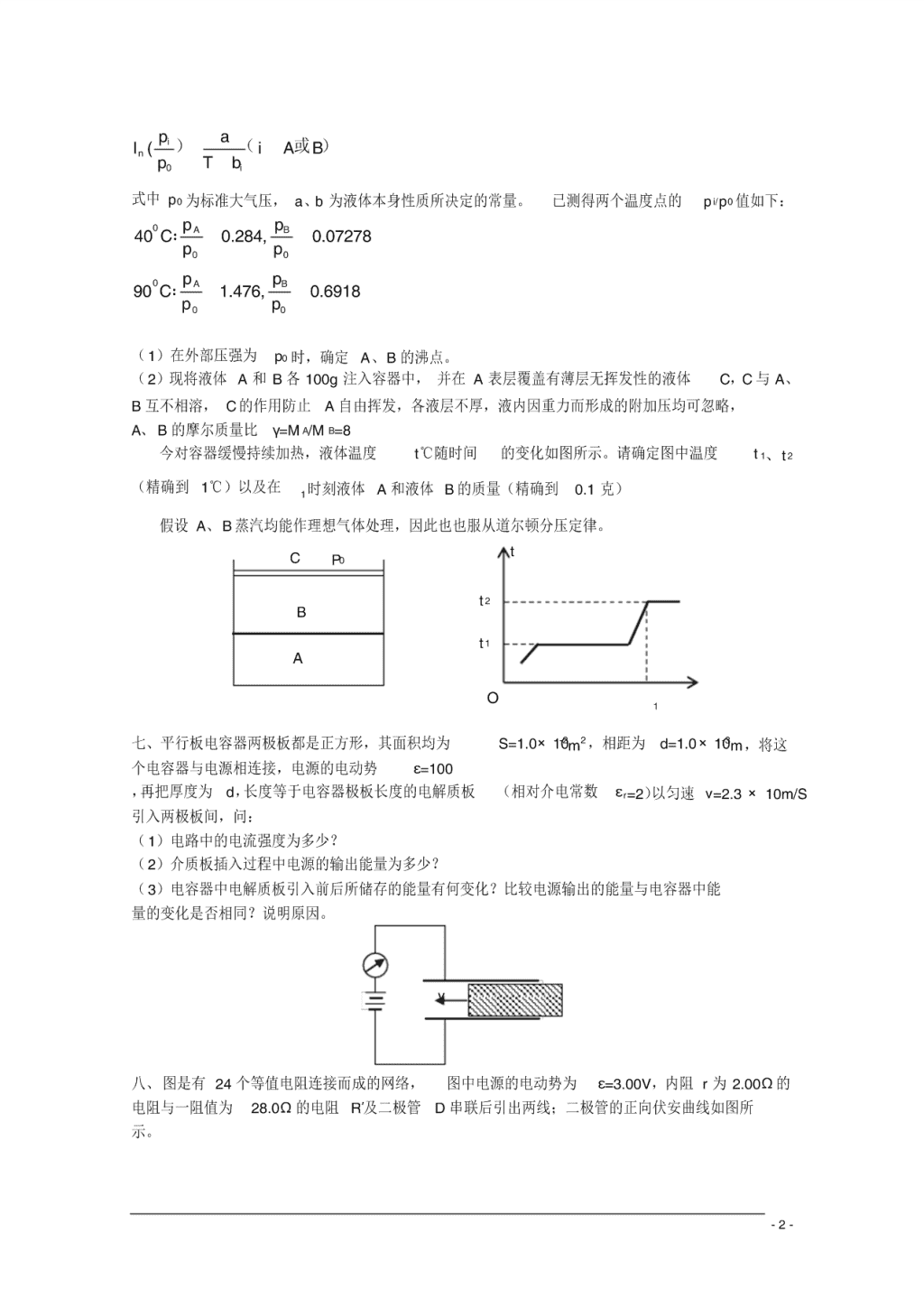 六、液体 A、B 互不相溶，它们的饱和气压 p 与温度 T 的关系是 k+1 k 2 1 2n-1 2n ν0 ν A θ B 0l l B O A 2l - 2 - 0 ( i n i p al i A B p T b ） （ 或 ） 式中 p0 为标准大气压， a、b 为液体本身性质所决定的常量。 已测得两个温度点的 p i/p0 值如下： （1）在外部压强为 p0 时，确定 A、B 的沸点。 （2）现将液体 A 和 B 各 100g 注入容器中， 并在 A 表层覆盖有薄层无挥发性的液体 C，C 与 A、 B 互不相溶， C的作用防止 A 自由挥发，各液层不厚，液内因重力而形成的附加压均可忽略， A、 B 的摩尔质量比 γ=M A/M B=8 今对容器缓慢持续加热，液体温度 t℃随时间 的变化如图所示。请确定图中温度 t 1、t 2 （精确到 1℃）以及在 1时刻液体 A 和液体 B 的质量（精确到 0.1 克） 假设 A、B 蒸汽均能作理想气体处理，因此也也服从道尔顿分压定律。 七、平行板电容器两极板都是正方形，其面积均为 S=1.0×10-2m2，相距为 d=1.0×10-3m，将这 个电容器与电源相连接，电源的电动势 ε=100 ，再把厚度为 d，长度等于电容器极板长度的电解质板 （相对介电常数 εr=2）以匀速 ν=2.3 × 10m/S 引入两极板间，问： （1）电路中的电流强度为多少？ （2）介质板插入过程中电源的输出能量为多少？ （3）电容器中电解质板引入前后所储存的能量有何变化？比较电源输出的能量与电容器中能 量的变化是否相同？说明原因。 八、图是有 24 个等值电阻连接而成的网络， 图中电源的电动势为 ε=3.00V，内阻 r 为 2.00Ω的 电阻与一阻值为 28.0Ω的电阻 R′及二极管 D 串联后引出两线；二极管的正向伏安曲线如图所 示。 P0 C B A O t t 2 t 1 1 ν 0 0 40 0.284, 0.07278 90 1.476, 0.6918 A B A B p pC p pC 0 0 0 0 ： p p ： p p - 3 - （1）若将 P、Q 两端与图中电阻网络 E、G 两点相接，测得二极管两端的电压为 0.86V，求电 阻网络两点 E与 G 的电压。 （2）若将 P、Q 两端与图中电阻网络 B、D 两点相接，求同二极管 D 的电流 ID 和网格中 E、G 间的电压 UEG。 九、考虑不用发射到绕太阳运动的轨道上的方法，要在太阳系建立一个质量为 m 静止的太空 站。这个太空站有一个面向太阳的大反射面（反射系数为 1），来自太阳的辐射功率 L 产生的 辐射压力使太空站受到一个背离太阳的力，此力与质量为 M S的太阳对太空站的万有引力方向 相反，大小相等，因而太空站处于平衡状态。忽略行星对太空站的作用，求： （1）此太空站的反射面面积 A； （2）平衡条件和太阳与太空站之间的距离是否有关？ （3）设反射面是边长为 d 的正方形，空间站的质量为 106kg，确定 d 之值。已知太阳的辐射 功率是 3.77 ×1026W。太阳质量为 1.99 × 1030kg。 F E H D C B A G R2 R3 R4 R6 R5 R7 R1 R9 R8 R10 R11 R12 R13 R14 R15 R16 R17 R18 R19 R20 R21 R22 R23 R24 1.6 1.0 100 50 10 I 0 /mA 0 U/V0.2 - 4 - 参考答案 一、□解Ⅰ 对一个正 n 边形，内角的度数是 ( 2)n n ，设每边的长度是 a（以五边形为例） A 顶点对着 B 质点运动到点 F 处， B 质点对着 C 顶点运动到了 G 处（如图） ，在△ BGF中用余 弦定理 FG2=（a-ν?t） 2+（ν?t） 2-2（ν?t ）（a-ν?t）cos ( 2)n n 舍去高阶小量 1 22 1 2 22 2 cos( ) 2 21 1 cos( ) nFG a v ta v ta n v t na a n V 因为 2 2[1 cos( )] 1v t n a n V 所以 2{1 [1 cos( )]} 2[1 cos( )] v t nFG a a n na FG v t n V V 每边边长的减短率为 2[1 cos( )]nv n 相遇时间 2 2[1 cos( )] (1 cos ) a at nv v n n □解Ⅱ 在整个运动过程中所有质点总是在一个正 n 形的顶点上（只是正 n 形不断变小） ，因 此 α和 θ不会变，即 α= n , θ= 2 n 。质点向着正 n 边形中点 O运动的速度为 cos sin / sin 2 v v v n al n 到达中点的时间 2 22 sin ( ) (1 cos ) l a at v v vn n 二、□解Ⅰ 这是一个比较复杂的运动，将此运动看成两个运动的合成：一个是 B 滑轮不动， 卷扬机以速度 ν0 收吊索；另一个是 AB 段吊索长度不变， B 滑块以 ν向右运动。第一个运动使 E G A D F C B θ ν O α - 5 - A 滑块得到了一个速度 ν1= 0 sin v 第二个运动使 A 滑块得到另一个速度 ν2=-cotθ·ν A 的真实速度 νA=ν1+ν2= 0 cos sin v v 将 A 的速度分解成沿吊索方向的分量 νAⅡ和垂直吊索方向的分量 Av 0 cos cos sinA v vv B 速度的垂直于吊索的分量 sinBv v 所以 A 相对于 B 垂直于吊索方向的速度 0 cos sinA B A v vv v v A 物体的向心加速度 2 2 0 0 cos / cos A Av va l l 分析 A 的受力情况可知 sin cos cos T mg N ma T N 联立，即可求得 T □解Ⅱ 以滑轮 B 为参照物， A 物体速度可看成水平方向的速度 ν和竖直方向的速度 ν ′的合 成，卷扬机虽然也有向左的速度 ν，但不影响吊索的速度，所以物体 A 沿吊索方向的速度亦为 ν 0。即 0 cos sinv v v 得 0 cos sin v vv A 速度垂直吊索的分量 0 sin cos cos sin Av v v v v 以下同解Ⅰ 三、如图，对第 k(k ≥2) 个滚珠进行受力分析，它受到左右两侧的压力分别记为 Nk-1 和 NK，还 受到管壁的经向弹力 P 和重力 W。建立如图直角坐标系， 只讨论在 x 方向上的合力为零的条件 则有 1 cos cos cos 0K KN W N Av ν′ν0 ν θ - 6 - 有图中几何关系可知 / 2 / 2n 所以有 α= 4n 同时有 ( 1) 2 4 (2 1) 4 k n n k n 将 α, β值代入式可得 1 (2 1)cos 4[ ] cos 4 k k k nN N W n 即有 2 1 3 2 1 3cos 4[ ] cos 4 5cos 4[ ] cos4 (2 1)cos 4[ ] cos 4 k k nN N W n nN N W n k nN N W n L L 两边相加后可得 1 3 5 2 1cos cos cos 4 4 4{ } cos4 k k n n nN N W n L （ ） 对第一个钢珠受力分析不难得到 1 cos 4[ ] cos4 nN W n 因此 x A y P W Nk β α α Nk-1 θ - 7 - 1 1 1 1 2 1[ cos ] 4 cos 4 [ 2cos sin ]2 1 4 4cos 4 2sin 4 1{ [sin sin ]} 2 2sin 4 sin 2 2sin 4 k i k k k i i k i i nN W n i i n n n n i i n n k n n （ ） （ ）（ ） 2n （ ） 2n 所以 sin 2( ) sin 2 k k nN W n 四、 如图， 小球沿半圆轨道运动到 B′位置时， 有机械能受恒定理可知， 它应具有向上速度 ν 0。 若 ν 0 足够大，则小球可沿较小半圆轨道击中 A 点。若 ν 0 较小，则可能在较小半圆轨道的某 C点脱离半圆轨道改取斜抛轨道， 也有可能击中 A点， 这种方式对应的 ν 0 即为所求的最小值。 为 C点引入方位角。小球在 C点脱离圆轨道故此时绳中张力恰为零。小球速度 ν 应满足以下 关系式 2sin /mg F mv l心 式中 m为小球质量。 l 为半圆轨道半径，又由机械能受恒可得 2 2 0 1 1 sin 2 2 mv mv mgl 上述两式可解得 2 0sin 2 v gl 建立如图坐标 O-xy 系，小球在点 C时刻定为 t=0 ，则 C点后斜抛运动的 x、 y 分运动为 2 cos ( sin ) 1sin ( cos ) 2 x l v t y l v t gt 消去 t ，可得 - 8 - 2 2 2 2 2 cos ( cos ) 1 ( cos )sin [ ] sin 2 sin 1 ( cos )cos 2sin ( cos ) sin sin v x l x ly l g v v xglx ll l l v 由前面所述，可得 2 sinv gl 代入上式可得 2 3 ( cos )cos ( cos ) sin sin 2sin x x y l l l 要求小球与 A 点相遇，即抛物线轨道需过 x= l ，因此 2 3 (1 cos )cos (1 cos )0 sin sin 2sin 可展开并逐渐化简为 4 2 2 2 2 2 2 2 2 2 2 3 2 2 3 2 2sin sin cos 2sin cos 1 2cos cos 0 2sin (sin cos ) 2cos (1 sin ) 1 cos 0 2sin 2cos 1 cos 0 2 2cos 2cos 1 cos 0 最后得 cos θ的三次方程式 2 31 3cos 2cos 0 其解为 1cos 2 因此 3sin 2 与前面的 2 0sin / 3v gl 联立，即算得最小 ν 0 值为 0 3 3 / 2v gl 。 五、如图所示，斜线覆盖的内圆是地球，其外为飞船离 开后的椭圆轨道， 再外面是飞船与宇航站开始的圆轨道， 最外面是飞船的新轨道。地球质量记为 Me，飞船被发射前，它与宇航站一起运动的速度为 u， 则有 2 2 ( )( ) ( ) eG M m MM m u nR nR B B′ A y C ν0 x θ O 2 ll - 9 - 得 eGMu nR 飞船发射后的瞬间，飞船的速度记为 u，宇航站的速度记为 V，根据动量受恒有： ( )M m u MV mv 即得所需要的比值为 V um M u v 于是问题转化为求 v 和 V 分离后飞船近地点与地心相距 nR，速度大小为 ν，远地点与地心相距 8nR，飞船速度大小记 为 ν′，则由开普勒第二定律和动能受恒得 2 2 8 1 1 2 2 8 e e vnR v nR GM m GM mmv mv nR nR 由此解得 4 4 3 3 eGMv u nR 分离后宇航站远地点与地心间距离设为 nR，速度大小记为 V。近地点与地心间距 r ，速度大小 为 V℃。同样可列方程组： 2 2 1 1 2 2 e e V nR V r GMMMVGMM rMV nR 可解得 2 ( ) eGMrV nR r nR 由可以看出，若求得 r 便可算出 m/M值 为求 r ，可利用开普勒第三定律，设飞船新轨道的周期为 t ，而它的半轴长则为 (8 ) 2 nR nR ； 宇航站新轨道周期设为 T，而它的半长轴则为 ( ) 2 nR r ，有 3 3 2 2 (8 ) ( )nR nR nR r t T 即 3 29 ( ) ( ) nR t nR r T - 10 - 飞船运行一周后恰好与宇航站相遇，因此 t=Kt k=1 、 2、3、⋯⋯ 代入上式后便可得 2 3 2 3 (9 )k nRr k 宇航站不能与地球相碰，否则它不可能再与飞船相遇，故要求 r>R 代入上式，并考虑到 n=1.25, 可得 k≤11 现由上式计算 m/M值 2/3 2[ 1] ( )( ) ( ) (1 4/ 3) 23 3 3 2(9 ) ( ) r nR rm V u M u v r k nR r 要求 m/M>0 因此 k2/3 >9/2 即 k≥10 可见 k 取值只可为 k=10 或 k=11 因此 0.048m M 或 0.153 六、（ 1）沸点即 0 1ip p 时的温度，由于 0 ( ) 0i n pl p ，可得沸点 i i i aT b 。对于 A 0.284 [ ] (273.15 40) 1.476 [ ] (273.15 90) A n A A n A al b al b 解之得 3748.49 , 10.711A Aa K b 同理得 5121.64 , 13.735B Ba K b ν m M - 11 - 据此可得液体 A、B 沸点 0 0 349.45 77 372.89 100 A B T K C T K C （2）系统有两次沸腾现象， t 1、t 2 是沸点。第一次应发生在 A、 B 交界面处，界面上气泡内压 强等于 A、B 的饱和气压之和，其值先达到 p0，此时沸腾温度 t 1 低于 A、B 各自的沸点。有 1 1 0( ) ( )A Bp t p t p 由于 ( / ) 0 iai T bip e p 令 1 1 0 0 1, 273.15,T t t t t 满足即 代入 0, , , ,A A B Ba b a b t 值，采用二分逼近方法取值，可得 t 1=67℃ A、B 交界面一消失，第一次沸腾结束。容器内仅剩一种液体，要加热到 t 2 该液体的沸点才出 现第二次沸腾。 T2 必为 100℃或者 77℃。 在温度 t 1 的沸腾过程中，从交界面出升离的气泡中， A、B 的饱和气质量比 1 1 2 2 ( ) ( )8 ( ) ( ) A A A A A B B B B B m M p t p t m M p t p t 由（ 2）式可得 t 1 时， A、 B的饱和气压： 1 0 0( ) 0.734 , 0.267A Bp t p p p 因此 22.0A B m m 这表明 A蒸发质量是 B的 22 倍，液体 A 的 100 克全部蒸发掉，液体 B仅剩 4.5 克，可见在 t 1 时刻容器中，液体 A 的质量为 0，液体 B 的质量为 95.5 克，因此 t 2=100℃ 七、（ 1）在电介质匀速插入过程中，电容不断增加经过 tV 之后，电容为 0 0 4 4 ( 1) 4 r r Sv tSv tC C Kd Kd Sv tC Kd VV V 电容增量之值 0 ( 1) 4 r Sv tC C C Kd VV 因 Q=Cε，故电容器上电量相应增加之值为 - 12 - ( 1) 4 r Sv tQ C Kd VV V 所以充电电流 2 2 9 3 9 ( 1) 4 (2 1) 10 2.3 10 100 4 3.14 9 10 1.0 10 2 10 ( ) r SvQI t Kd A V V （2）电源输出的电能 2 9 7 2 102 10 100 9 10 ( ) 2.3 10 W I t J （3）介质未插入时，电容所贮电能为 2 2 1 0 2 2 9 3 7 1 1 2 2 4 1 10 100 2 4 3.14 9 10 10 4.43 10 ( ) SW C Kd J 插入介质后，电容所贮电能增加 2 2 7 0 0 0 1 1( ) 4.43 10 ( ) 2 2rW C C C JV 所以电源输出能量 W>?W，由题设电源内阻，线路电阻均不计，那么电源多输出的电能 W-?W 到什么地方去了。把介质插入电容器之间时，在介质板上产生极化电荷，极板上自由电贺对 极化电荷产生吸引力，在忽略介质板和电容器极板之间的摩擦力时，要使介质板匀速地插入 电容器中去，必须在加一个外力与此吸引力相平衡。因此，在介质板匀速插入电容器时，外 力做负功，使电源输出的一部分能量 W-?W变成了其它形式的能量。 八、（ 1）当引线两端 P、Q 与电阻网格 E、G两点连接时，二极管两端的电压 UD1=0.86V ，此时 对应的电流从图中查得为 25.0mA，则 E、G两点间的电压为 1 1 1 3 0.025 (28.0 2) 0.86 1.39( ) EG DU I R U rI V 考虑到对称性，网格 EG两端的等效电阻 REG可由图表示 , 其值 REG=13R/3 - 13 - 而 1 0 1 1 1 18 15 12 0 1 0 55.6( ) 7 29.9( ) 13 3( ) ( )( )( ) (1 6 / 7) 2 7 2 2 13 0.695( ) 14 EG EG EG EA UR I R R I I IU R R R R I R V 从图可看出 EA EGU U 的一半 , 即 0.695V (2) 当引线两端 P、Q 与电阻网格 B、D 两点相接时 , 由图求得等效电阻 RBD与 R0 关系 , 并代入 R0 的阻值 0 5 5 29.9 7 7 21.4( ) BDR R 通过二极管 D的电流 i D与二极管两端的电压关系 2 2 ( )D D BDU I R R r 代入数据得 2 23 51.4D DU I g 这是一条联系 UD 与的 I D 直线方程 , 而 UD、 I D 同时又满足二极管伏安特性曲线中一直线 2 23 51.4D DU I g 与 二 极 管 伏 安 特 性 曲 线 的 纵 坐 标 即 为 二 极 管 的 电 流 , 由 图 读 出 2 40.5DI mA A R1 H G C E R2 R3 R4 R5 R6 R7 R8 R9 R10 R11 R12 R13 R14 R15 R16 R17 R18 R19 R20 R21 R22 R23 R24 F - 14 - 根据对称性 , 图中 ,M、P 两点等势 , N 、Q两点等势 , 流过 R18、R22 及 R3、R7 流过电阻的电流均为 零, 因此 E、G间的电势差与 M、 N两点之间的电势差相等 2 4 1 11 2 4 1 8 1 2 0 ( )2 [ ] 7 2 2 3 52( ) 7 2 D EG MN D I R RU U R R R R R R I R V g g g 九、 (1) 设空间站与太阳距离为 r, 则太阳辐射在空间站反射面单位面积内的功率即为光强 Ф= 4 L r , 太阳对反射面产生的压强是光子的动量传递给反射面的结果 , 这一光压为 于是反射面受到的辐射压力 22 LF PA A r c辐射 太阳对太空站的万有引力为 2 SM mGF r引力 . 式中 G 为万有引力常数 . 在太空站处于平衡状态 时 , F F辐射 引力 即 2 22 SM mGL A r c r 这就得到 , 反射面面积 2 SGM mcA L (2) 有上面的讨论可知 , 由于辐射压力和太阳引力都与 r 2 成反比 , 因而平衡条件与太阳和空间站 的距离 r 无关 . (3) 若 A=d2, 并以题给数据代入前式得到 D B A H G C E R1 F R2 R3 R4 R5 R6 R7 R8 R9 R10 R11 R12 R13 R14 R15 R16 R17 R18 R19 R22 R23 R20 R24 R21 1.6 1.0 100 50 10 I 0 /mA 0 U/V0.2 - 15 - 11 2 2 30 6 8 26 4 2 2 6.67 10 / )(1.99 10 )(10 )(3.00 10 ) 3.77 10 2.58 10 SGMd L Nm kg kg kg m （