2018届高考物理第一轮总复习全程训练课练18实验：探究功与速度变化的关系　验证机械能守恒定律 15页

课练18　实验：探究功与速度变化的关系 验证机械能守恒定律 ‎1．在“探究功与速度变化的关系”的实验中，某实验研究小组的实验装置如图甲所示．木块从A点由静止释放后，在一根弹簧作用下弹出，沿足够长的木板运动到B点停下，记录此过程中弹簧对木块做的功为W1.O点为弹簧原长时所处的位置，测得OB的距离为L1.再用完全相同的2根，3根，…弹簧并在一起进行第2次，第3次，…实验并记录2W1,3W1，…及相应的L2，L3，…，用W－L图象处理数据，回答下列问题：‎ ‎　　‎ ‎(1)如图乙是根据实验数据描绘的W—L图象，图线不过原点的原因是________．‎ ‎(2)由图线得木块从A到O过程中克服摩擦力做的功是________W1.‎ ‎(3)W—L图象斜率的物理意义是________．‎ ‎2．某兴趣小组想通过物块在斜面上运动的实验探究“合外力做功和物体速度变化的关系”．实验开始前，他们提出了以下几种猜想：①W∝，②W∝v，③W∝v2.他们的实验装置如图甲所示，PQ为一块倾斜放置的木板，在Q处固定一个速度传感器(用来测量物体每次通过Q点时的速度)，每次实验，物体从不同初始位置处由静止释放．‎ 同学们设计了以下表格来记录实验数据．其中L1、L2、L3、L4……代表物体分别从不同初始位置处无初速度释放时初始位置到速度传感器的距离，v1、v2、v3、v4……表示物体每次通过Q点的速度.‎ 实验次数 ‎1‎ ‎2‎ ‎3‎ ‎4‎ ‎……‎ L L1‎ L2‎ L3‎ L4‎ ‎……‎ v v1‎ v2‎ v3‎ v4‎ ‎……‎ 他们根据实验数据绘制了如图乙所示的L—v图象，并得出结论W∝v2.‎ ‎(1)你认为他们的做法是否合适？________.‎ ‎(2)你有什么好的建议？________.‎ ‎(3)在此实验中，木板与物体间摩擦力的大小________(填“会”或“不会”)影响探究出的结果．‎ ‎3．某实验小组采用如图甲所示的装置探究功与速度变化的关系，小车在橡皮筋的作用下弹出后，沿木板滑行．‎ ‎(1)实验中木板略微倾斜，这样做________．‎ A．是为了释放小车后，小车能匀加速下滑 B．是为了增大小车下滑的加速度 C．可使得橡皮筋做的功等于合力对小车做的功 D．可使得橡皮筋松驰后小车做匀速运动 ‎　　‎ ‎(2)实验中，打点计时器使用的交流电频率为50 Hz.某同学打出的一段纸带如图乙所示，则小车匀速运动时的速度大小为________m/s(计算结果保留两位有效数字)．‎ ‎(3)实验中，某同学分别用1根、2根、…、5根相同橡皮筋进行实验，测得小车匀速运动时的速度分别为0.52 m/s、0.78 m/s、0.96 m/s、1.08 m/s、1.22 m/s.请根据实验数据图丙所示的在坐标系中画出W－v的关系图线．‎ ‎(4)根据图线可知，对W与v的关系的猜想肯定不正确的是________．‎ A．W∝ B．W∝ C．W∝v2 D．W∝v3‎ ‎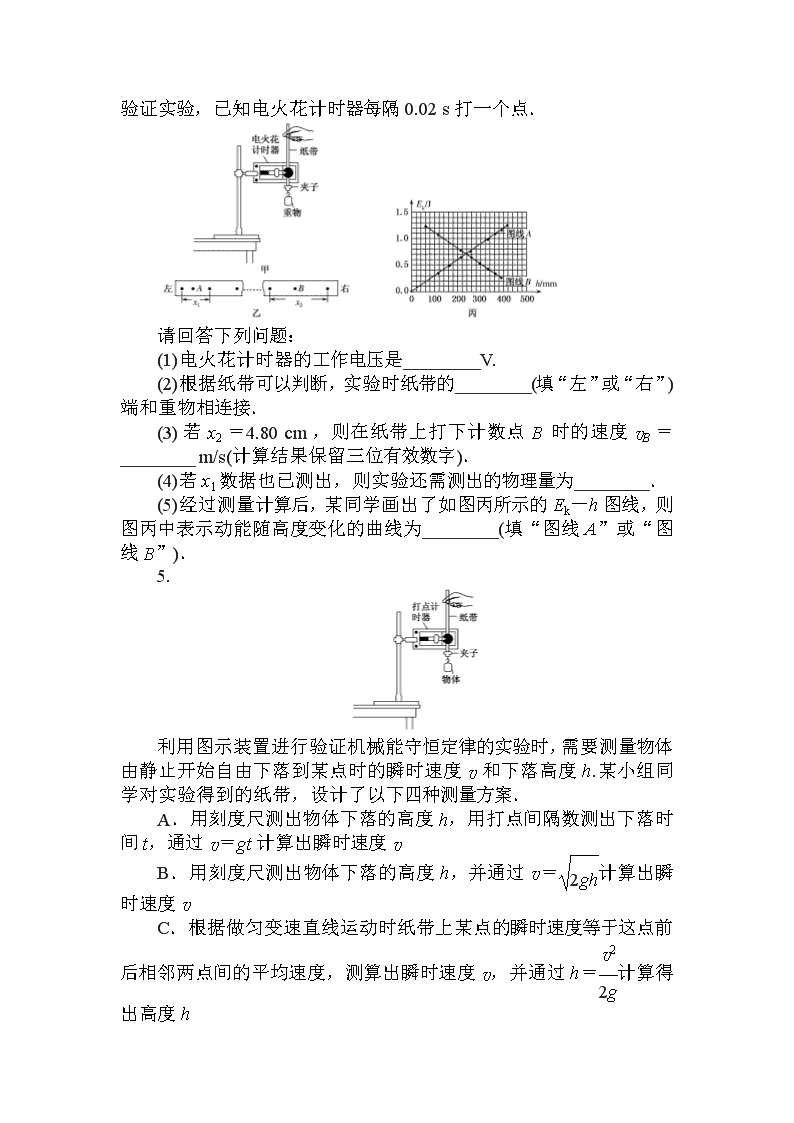4．某同学安装如图甲所示的实验装置，验证机械能守恒定律．如图乙所示是该实验得到的一条点迹清晰的纸带，现要取A、B 两点来验证实验，已知电火花计时器每隔0.02 s打一个点．‎ ‎　　‎ 请回答下列问题：‎ ‎(1)电火花计时器的工作电压是________V.‎ ‎(2)根据纸带可以判断，实验时纸带的________(填“左”或“右”)端和重物相连接．‎ ‎(3)若x2＝4.80 cm，则在纸带上打下计数点B时的速度vB＝________ m/s(计算结果保留三位有效数字)．‎ ‎(4)若x1数据也已测出，则实验还需测出的物理量为________．‎ ‎(5)经过测量计算后，某同学画出了如图丙所示的Ek－h图线，则图丙中表示动能随高度变化的曲线为________(填“图线A”或“图线B”)．‎ ‎5.‎ 利用图示装置进行验证机械能守恒定律的实验时，需要测量物体由静止开始自由下落到某点时的瞬时速度v和下落高度h.某小组同学对实验得到的纸带，设计了以下四种测量方案．‎ A．用刻度尺测出物体下落的高度h，用打点间隔数测出下落时间t，通过v＝gt计算出瞬时速度v B．用刻度尺测出物体下落的高度h，并通过v＝计算出瞬时速度v C．根据做匀变速直线运动时纸带上某点的瞬时速度等于这点前后相邻两点间的平均速度，测算出瞬时速度v，并通过h＝计算得出高度h D．用刻度尺测出物体下落的高度h ‎，根据做匀变速直线运动时，纸带上某点的瞬时速度等于这点前后相邻两点间的平均速度，测算出瞬时速度v ‎(1)以上方案中只有一种正确，正确的是________(填入相应的字母)．‎ ‎(2)在该实验中，有几个注意点，以下描述正确的是________．‎ A．为减小摩擦阻力，需要调整打点计时器的限位孔，使它与纸带在同一竖直线上 B．可以选用质量很大的物体，先用手托住，等计时器通电后再释放物体 C．只有选第1、2两点间隔小于或约2 mm的纸带才代表打第1点时的速度为零 D．实验结果如果正确合理，得到的动能增加量应略大于重力势能的减少量 ‎6．用如图甲所示的实验装置验证m1、m2组成的系统机械能守恒，m2从高处由静止开始下落，在m1拖着的纸带上打出一系列的点，对纸带上的点迹进行测量，即可验证机械能守恒定律．图乙给出的是实验中获取的一条纸带：0是打下的第一个点，每相邻两计数点间还有4个点未标出，计数点间的距离如图乙所示．已知m1＝50 g，m2＝150 g，g取10 m/s2，交流电源的频率为50 Hz，不考虑各处摩擦力的影响，结果保留两位小数．‎ ‎　　‎ ‎(1)在纸带上打下计数点5时m2的速度v＝________m/s.‎ ‎(2)在打点0～5过程中系统动能的增量ΔEk＝________J，系统重力势能的减少量ΔEp＝________J.‎ ‎(3)若某同学作出v2－h图象如图丙所示，则该同学测得的重力加速度g＝________m/s2.‎ ‎7．如图甲所示的装置叫做阿特伍德机，是英国数学家和物理学家阿特伍德(G·Atwood 1746～1807)创制的一种著名力学实验装置，用来研究匀变速直线运动的规律．某同学对该装置加以改进后用来验证机械能守恒定律，如图乙所示．‎ ‎(1)实验时，该同学进行了如下步骤：‎ ‎①将质量均为M(A含挡光片、B含挂钩)的重物用绳连接后，跨放在定滑轮上，处于静止状态，测量出________(填“A的上表面”、“A的下表面”或“挡光片中心”)到光电门中心的竖直距离h.‎ ‎②在B的下端挂上质量为m的物块C，让系统(重物A、B以及物块C)中的物体由静止开始运动，光电门记录挡光片挡光的时间为Δt.‎ ‎③测出挡光片的宽度d，计算有关物理量，验证机械能守恒定律．‎ ‎(2)如果系统(重物A、B以及物块C)的机械能守恒，应满足的关系式为________(已知重力加速度为g)．‎ ‎(3)引起该实验系统误差的原因有________(写一条即可)．‎ ‎(4)验证实验结束后，该同学突发奇想：如果系统(重物A、B以及物块C)的机械能守恒，不断增大物块C的质量m，重物B的加速度a也将不断增大，那么a与m之间有怎样的定量关系？a随m增大会趋于一个什么值？请你帮该同学解决：‎ ‎①写出a与m之间的关系式：________(还要用到M和g)；‎ ‎②a的值会趋于________．‎ ‎　 　 　　 　　　　　　　　　　　　　　　　　　　　‎ ‎1．(2016·江苏单科)某同学用如图甲所示的装置验证机械能守恒定律．一根细线系住钢球，悬挂在铁架台上，钢球静止于A点．光电门固定在A的正下方，在钢球底部竖直地粘住一片宽度为d的遮光条．将钢球拉至不同位置由静止释放，遮光条经过光电门的挡光时间t可由计时器测出，取v＝作为钢球经过A点时的速度．记录钢球每次下落的高度h和计时器示数t，计算并比较钢球在释放点和A点之间的势能变化大小ΔEp与动能变化大小ΔEk，就能验证机械能是否守恒．‎ ‎　　‎ ‎(1)用ΔEp＝mgh计算钢球重力势能变化的大小，式中钢球下落高度h应测量释放时的钢球球心到__________之间的竖直距离．‎ A．钢球在A点时的顶端 B．钢球在A点时的球心 C．钢球在A点时的底端 ‎(2)用ΔEk＝mv2计算钢球动能变化的大小．用刻度尺测量遮光条宽度，示数如图乙所示，其读数为__________ cm.某次测量中，计时器的示数为0.010 0 s，则钢球的速度为v＝__________ m/s.‎ ‎(3)下表为该同学的实验结果：‎ ΔEp(×10－2 J)‎ ‎4.892‎ ‎9.786‎ ‎14.69‎ ‎19.59‎ ‎29.38‎ ΔEk(×10－2 J)‎ ‎5.04‎ ‎10.1‎ ‎15.1‎ ‎20.0‎ ‎29.8‎ 他发现表中的ΔEp与ΔEk之间存在差异，认为这是由于空气阻力造成的．你是否同意他的观点？请说明理由．‎ ‎________________________________________________________________________‎ ‎(4)请你提出一条减小上述差异的改进建议．‎ ‎________________________________________________________________________‎ ‎2．(2017·湖南衡阳联考)‎ 某同学为探究合力做功与物体动能改变的关系，设计了如下实验，他的操作步骤是：‎ ‎①按图甲摆好实验装置，其中小车质量M＝0.4 kg，钩码总质量m＝0.1 kg.‎ ‎②先接通打点计时器的电源(电源频率f＝50 Hz)，然后释放小车，打出一条纸带．‎ ‎(1)经过多次重复实验，他从打出的多条纸带中选出一条打点清晰的，如图乙所示．把打下的第一点记作0，然后依次取若干个计数点，相邻计数点间还有4个点未画出，用厘米刻度尺测得各计数点到0点距离分别为d1＝0.041 m，d2＝0.055 m，d3＝0.167 m，d4＝0.256 m，d5＝0.360 m…他把钩码重量(当地重力加速度g＝9.8 m/s2)作为小车所受合力，算出0点到第4个计数点合力做功W＝________J，打下第4个计数点时小车动能Ek＝________J．(结果保留三位有效数字)‎ ‎(2)此实验探究的结果，他未能得到“合力对物体做的功等于动能的变化”，且误差很大，主要原因有________________________．(只需答一条)‎ ‎3．(2017·山东济南检测)如图甲是某同学验证动能定理的实验装置．其实验步骤如下：‎ a．易拉罐内盛上适量细砂，用轻绳通过滑轮连接在小车上，小车连接纸带．调整木板倾角，让小车沿木板匀速下滑．‎ b．取下轻绳和易拉罐，测出易拉罐和细砂的总质量m及小车质量M.‎ c．取下轻绳和易拉罐后，换一条纸带，将小车由静止释放，打出的纸带如图乙(中间部分未画出)，O为打下的第一个点．已知打点计时器的打点频率为f，重力加速度为g.‎ ‎(1)步骤c中小车所受的合力为________．‎ ‎(2)为验证从O→C 过程中小车所受的合力做的功与小车动能变化量的关系，测出B、D间距离为x0，O、C间距离为x1，则打C点时小车的速度为________，需要验证的关系式为________．(用所测物理量的字母代号表示)‎ ‎4．(2017·北师大附中一模)质量为1 kg的重物自由下落，通过打点计时器在纸带上记录下运动的过程，打点计时器所接电源为6 V、50 Hz的交流电源．如图1所示，打出的纸带上O点为重物自由下落时打点的起点，选取的计数点A、B、C、D、E、F、G依次间隔一个点(图中未画出)，各计数点与O点的距离依次为31.4、70.6、125.4、195.9、282.1、383.8、501.2，单位为mm，重力加速度为9.8 m/s2.(计算结果均保留两位小数)‎ ‎(1)求出打B、C、D、E、F各点时重物的速度并填入下表.‎ 计数点 B C D E F 速度/(m·s－1)‎ ‎(2)求出重物从起点下落到打下各计数点过程中重力所做的功并填入下表.‎ 计数点 B C D E F 功/J ‎(3)适当选择坐标轴，在图2中作出重力做的功WG与速度v2的相关量之间的关系图，以便探究做功与速度的关系．由作出的图线可得重力所做的功与________成________关系．‎ ‎5．(2017·云南毕业统测)‎ 如图所示，质量分别为m1和m2的物块A和B ‎，分别系在一条跨过定滑轮的轻质细绳两端，已知m1>m2,1、2是两个计时光电门，不计滑轮质量和摩擦，重力加速度为g.用此装置验证机械能守恒定律．‎ ‎(1)物块B上固定有一宽度为d的挡光条，实验中记录下挡光条通过1、2两光电门的时间分别为Δt1和Δt2，此外还需要测量的物理量是____________．‎ ‎(2)用已知量和测量量写出验证机械能守恒的表达式：________________________.‎ ‎6．(2017·吉林三模)利用气垫导轨验证机械能守恒定律，实验装置如图1所示，水平桌面上固定一倾斜的气垫导轨，导轨上A点处有一带长方形遮光片的滑块，总质量为M，左端由跨过轻质光滑定滑轮的细绳与一质量为m的小球相连；遮光片两条长边与导轨垂直；导轨上B点有一光电门，可以测量遮光片经过光电门时的挡光时间t，用d表示A点到光电门B点的距离，b表示遮光片的宽度，将遮光片通过光电门的平均速度看作滑块通过B点时的瞬时速度，实验时滑块在A点由静止开始运动．‎ ‎　　‎ ‎(1)用游标卡尺测量遮光片的宽度b，结果如图2所示，由此读出b＝________mm.‎ ‎(2)滑块通过B点的瞬时速度可表示为________．‎ ‎(3)某次实验测得倾角θ＝30°，重力加速度用g表示，滑块从A点到达B点时小球和滑块(包括遮光片)组成的系统动能增加量可表示为ΔEk＝________，系统的重力势能减少量可表示为ΔEp＝________，在误差允许的范围内，若ΔEk＝ΔEp，则可认为系统的机械能守恒．‎ ‎(4)‎ 在上次实验中，某同学改变A、B间的距离，作出的v2—d图象如图所示，并测得M＝m，则重力加速度g＝________ m/s2.‎ ‎7．(2017·黄岗中学模拟)如图甲所示，一位同学利用光电计时器等器材做“验证机械能守恒定律”的实验．有一直径为d、质量为m的金属小球从A处由静止释放，下落过程中能通过A处正下方、固定于B处的光电门，测得A、B间的距离为H(H≫d)，光电计时器记录下小球通过光电门的时间为t，当地的重力加速度为g.则：‎ ‎(1)如图乙所示，用游标卡尺测得小球的直径d＝________ mm.‎ ‎(2)小球经过光电门B时的速度表达式为________．‎ ‎(3)多次改变高度H，重复上述实验，作出随H的变化图象如图丙所示，当图中已知量t0、H0和重力加速度g及小球的直径d满足表达式________时，可判断小球下落过程中机械能守恒．‎ ‎(4)实验中发现动能增加量ΔEk总是稍小于重力势能减少量ΔEp，增加下落高度后，则ΔEp－ΔEk将________(填“增大”、“减小”或“不变”)．‎ 课练18　实验：探究功与 速度变化的关系 验证机械能守恒定律1.解题思路：(1)木块从A到B根据能量守恒定律可得W－Wf＝FfL，所以图象不过原点的原因是在AO段还有摩擦力做功．‎ ‎(2)由图知图象两点坐标为(0.06 cm,1W1)、(0.42 cm,5W1)代入W－Wf＝FfL解得木块从A到O过程中克服摩擦力做的功为W1.‎ ‎(3)由W－Wf＝FfL知图象的斜率为木块所受摩擦力．‎ 答案：(1)未计算AO间的摩擦力做功 ‎(2)　(3)木块所受摩擦力 ‎2．解题思路：(1)采用表格方式记录数据，合理绘制的L—v图象是曲线，不能得出结论W∝v2，所以他们的做法不合适．(2)为了更直观地看出L和v的变化关系，应该绘制L—v2图象．(3)重力和摩擦力的总功W也与距离L成正比，因此不会影响探究的结果．‎ 答案：(1)不合适　(2)应进一步绘制L—v2图象　(3)不会 ‎3．解题思路：‎ ‎(1)该实验中要使橡皮筋对小车所做功为合外力的功，应当进行平衡摩擦力的操作，这样操作可以使橡皮筋松弛后，小车能做匀速运动，从而根据纸带求出小车匀速时的速度大小(加速运动的最大速度)，故A、B错误，C、D正确．‎ ‎(2)点距均匀时的速度为匀速运动时的速度，因此有v＝＝ m/s＝2.0 m/s.‎ ‎(3)用描点法得出图象如图所示．‎ ‎(4)图象基本为一条抛物线，因此根据数学知识可知W∝一定是不正确的，故B错误．‎ 答案：(1)CD　(2)2.0　(3)如图所示　(4)B ‎4．解题思路：(2)从纸带上可以发现从左到右，相邻的计数点的距离越来越大，说明速度越来越大，纸带与重物相连接的一端先打出点，速度较小，所以实验时纸带的左端通过夹子和重物相连接．‎ ‎(3)纸带随重物一起做匀加速直线运动，根据匀变速直线运动的推论得：打出B点时纸带运动的瞬时速度为vB＝＝ m/s＝1.20 m/s.‎ ‎(4)若x1数据已测出，则可求出在纸带上打下计数点A时的速度，进而可求出A、B两点动能的变化量，要验证机械能守恒定律，则还要求出重力势能的变化量，所以还要测出A、B之间的距离hAB.‎ ‎(5)因重物在下落过程中做匀加速直线运动，所以高度越来越小，速度越来越大，动能越来越大，故图丙中表示动能随高度变化的曲线为图线B.‎ 答案：(1)220　(2)左　(3)1.20　(4)A、B之间的距离或hAB　(5)图线B ‎5．解题思路：(1)物体由静止开始自由下落过程中受到空气阻力和纸带与打点计时器的摩擦阻力作用，不是自由落体运动，v＝gt和v＝都是自由落体运动的公式．故A、B错误．物体下落的高度是用刻度尺测量的，不是计算得来的，故C错误．‎ ‎(2)选项B中物体质量并不是越大越好，且应用手拉住纸带而不是用手托住物体．选项D中由于摩擦不可能完全消除，实验结果如果正确合理，得到的动能增加量应略小于重力势能的减少量，A、C符合实验要求．‎ 答案：(1)D　(2)AC ‎6．解题思路：(1)v＝ m/s＝2.40 m/s.‎ ‎(2)ΔEk＝(m1＋m2)v2＝0.58 J，ΔEp＝(m2－m1)gh＝0.60 J.‎ ‎(3)根据ΔEk＝ΔEp，得gh＝，则g＝ m/s2，g＝9.70 m/s2.‎ 答案：(1)2.40　(2)0.58　0.60　(3)9.70‎ ‎7．解题思路：(1)①将质量均为M(A含挡光片、B含挂钩)的重物用绳连接后，跨放在定滑轮上，处于静止状态，测量出挡光片中心到光电门中心的竖直距离h.(2)重物A经过光电门的速度v＝，整个系统重力势能的减少量为mgh，动能增加量为(2M＋m)v2，则如果系统(重物A、B以及物块C)的机械能守恒，应满足的关系式为mgh＝(2M＋m)2.(3)引起该实验系统误差的原因有：绳子有质量；滑轮与绳子有摩擦；重物运动受到阻力作用．(4)①系统所受的合外力为F＝mg，则根据牛顿第二定律可知F＝(2M＋m)a，解得a＝；②根据a＝＝，当m逐渐变大时，a的值会趋于g.‎ 答案：(1)挡光片中心　(2)mgh＝(2M＋m)2　(3)绳子有质量(或滑轮与绳子有摩擦，或重物运动受到阻力作用，回答一个即可)　(4)①a＝　②重力加速度g 加餐练 ‎1．解题思路：(1)要考虑钢球重力势能的改变量大小，需要测量钢球球心下降的高度h，因此要测量钢球在释放点和A点时球心之间的竖直距离，选项B正确．‎ ‎(2)刻度尺的读数为1.50 cm，钢球的速度v＝＝ m/s＝1.50 m/s.‎ ‎(3)由动能定理可知，mgh－Wf＝ΔEk，即ΔEp－Wf＝ΔEk，ΔEp>ΔEk，所以空气阻力会造成ΔEp>ΔEk，但表中为ΔEk>ΔEp，因此不同意他的观点．‎ ‎(4)钢球球心和遮光条都绕悬点做圆周运动，但运动半径不同，因此分别测出光电门和球心到悬点的长度L和l，遮光条在光电门处的速度v＝，则钢球的速度v′＝·l，可以减小表中差异．‎ 答案：(1)B　(2)1.50(1.49～1.51都算对)　1.50(1.49～1.51都算对)‎ ‎(3)不同意，因为空气阻力会造成ΔEk小于ΔEp，但表中ΔEk大于ΔEp.‎ ‎(4)分别测出光电门和球心到悬点的长度L和l，计算ΔEk时，将v折算成钢球的速度v′＝v.‎ ‎2．解题思路：(1)根据题意，物体所受合力为：F＝mg＝0.98 N，‎ ‎0点到第4个计数点合力做功W＝Fs＝mgd4＝0.251 J 根据匀变速直线运动中中间时刻的瞬时速度等于该过程的平均速度，可求出打下第4个计数点时小车的速度大小 v4＝ 其中T＝5×0.02 s＝0.1 s d5＝0.360 m d3＝0.167 m 解得v4＝0.965 m/s 则打下第4个计数点时小车动能Ek＝Mv＝×0.4×0.9652 J＝0.186 J ‎(2)主要原因：①钩码质量太大；②没有平衡摩擦力．‎ 答案：(1)0.251　0.186　(2)见解析 ‎3．解题思路：(1)小车匀速下滑时受到重力、支持力、摩擦力和拉力作用，所受合力为零；撤去拉力后，其余力不变，故所受合力等于撤去的拉力mg.(2)匀变速直线运动的平均速度等于中间时刻的瞬时速度，故vC＝＝，小车的动能增加量为Mv＝，所受合力做的功为mgx1，故需要验证的关系式为mgx1＝.‎ 答案：(1)mg　(2)　mgx1＝ ‎4．解题思路：(1)打各点时重物的速度由公式v＝＝求出，则v B＝＝ m/s≈1.18 m/s，同理vC≈1.57 m/s，vD≈1.96 m/s，vE≈2.35 m/s，vF≈2.74 m/s.‎ ‎(2)由重力做的功W＝mgΔx可得，WB＝mg·OB＝1×9.8×70.6×10－3 J≈0.69 J，同理WC≈1.23 J，WD≈1.92 J，WE≈2.76 J，WF≈3.76 J.‎ ‎(3)由图可得重力所做的功与速度的平方成正比．‎ 答案：(1)1.18　1.57　1.96　2.35　2.74　(2)0.69　1.23　1.92　2.76　3.76　(3)如图所示　速度的平方正比 ‎5．解题思路：(1)通过连接在一起的A、B两物块验证机械能守恒定律，即验证系统的势能变化与动能变化是否相等，物块A、B通过细绳连接在一起，物块A下降的距离一定等于物块B上升的距离；物块A、B的速度大小总是相等的，故需要测量两光电门之间的距离h.(2)物块A下降h的同时，物块B上升h，它们的重力势能的变化量ΔEp＝(m1－m2)gh；物块A与B动能的变化量ΔEk＝(m1＋m2)，需要验证的是(m1－m2)gh＝(m1＋m2).‎ 答案：(1)两光电门之间的距离h ‎(2)(m1－m2)gh＝(m1＋m2) ‎6．解题思路：(1)宽度b为3 mm＋17×0.05 mm＝3.85 mm.(2)滑块通过B点的速度为vB＝.(3)滑块从A点到达B点时小球和滑块(包括遮光片)组成的系统动能增加量为ΔEk＝(M＋m)2＝，系统的重力势能减少量可表示为ΔEp＝mgd－Mgdsin30°＝ gd，比较ΔEp和ΔEk，若在实验误差允许的范围内相等，即可认为机械能是守恒的．(4)根据系统机械能守恒有(M＋m)v2＝gd，则v2＝gd，v2—d图象的图线斜率k＝g.由图象可知，k＝ m/s2＝4.8 m/s2，又M＝m，则有g＝×k＝9.6 m/s2.‎ 答案：(1)3.85　(2)　(3)　gd　(4)9.6‎ ‎7．解题思路：(1)由题图乙可知，主尺读数为7 mm，游标尺读数为5×0.05 mm＝0.25 mm，故小球直径d＝7 mm＋0.25 mm＝7.25 mm.(2)已知小球经过光电门B的时间和小球的直径，则小球经过光电门B时的速度v＝.(3)若减少的重力势能等于增加的动能，可以认为机械能守恒，则有mgH0＝mv2，即2gH0＝2，整理得2gH0t＝d2.(4)因为该过程中有克服阻力做功，而高度越高，阻力做功越多，故增加下落高度后，ΔEp－ΔEk增大．‎ 答案：(1)7.25　(2)v＝ ‎(3)3gH0t＝d2　(4)增大