河南省示范性高中罗山高中2020届高三物理复习热门考点专练（34）带电粒子在交变电场中的运动 9页

河南省示范性高中罗山高中2020届高三物理复习热门考点专练（34） ‎ 带电粒子在交变电场中的运动 带电粒子在交变电场中的运动分析，涉及电场知识、力学知识等内容，随着科技的发展及高考试题应用性、实践性的增强和提高，本训练点知识在整个电磁学中的位置愈加显得重要.通过训练，逐步掌握此类问题的分析方法.第11题为创新题，使我们了解本训练点知识在实践中的应用.‎ 一、选择题（每小题5分，共25分）‎ ‎1.在两金属板(平行）分别加上如图2—7—1中的电压，使原来静止在金属板中央的电子有可能做振动的电压图象应是（设两板距离足够大）‎ 图2—7—2(甲)‎ 图2—7—1‎ ‎2.有一个电子原来静止于平行板电容器的中间，设两板的距离足够大，今在t=0开始在两板间加一个交变电压，使得该电子在开始一段时间内的运动的v—t图线如图2—7—2(甲)所示，则该交变电压可能是图2—7—2(乙)中的哪些 图2—7—2（乙）‎ ‎3.一个匀强电场的电场强度随时间变化的图象如图2—7—3所示，在这个匀强电场中有一个带电粒子，在t=0时刻由静止释放，若带电粒子只受电场力的作用，则电场力的作用和带电粒子的运动情况是 图2—7—3‎ A.带电粒子将向一个方向运动 B.0~3 s内，电场力的冲量等于0，电场力的功亦等于0‎ C.3 s末带电粒子回到原出发点 D.2 s~4 s内电场力的冲量不等于0，而电场力的功等于0‎ ‎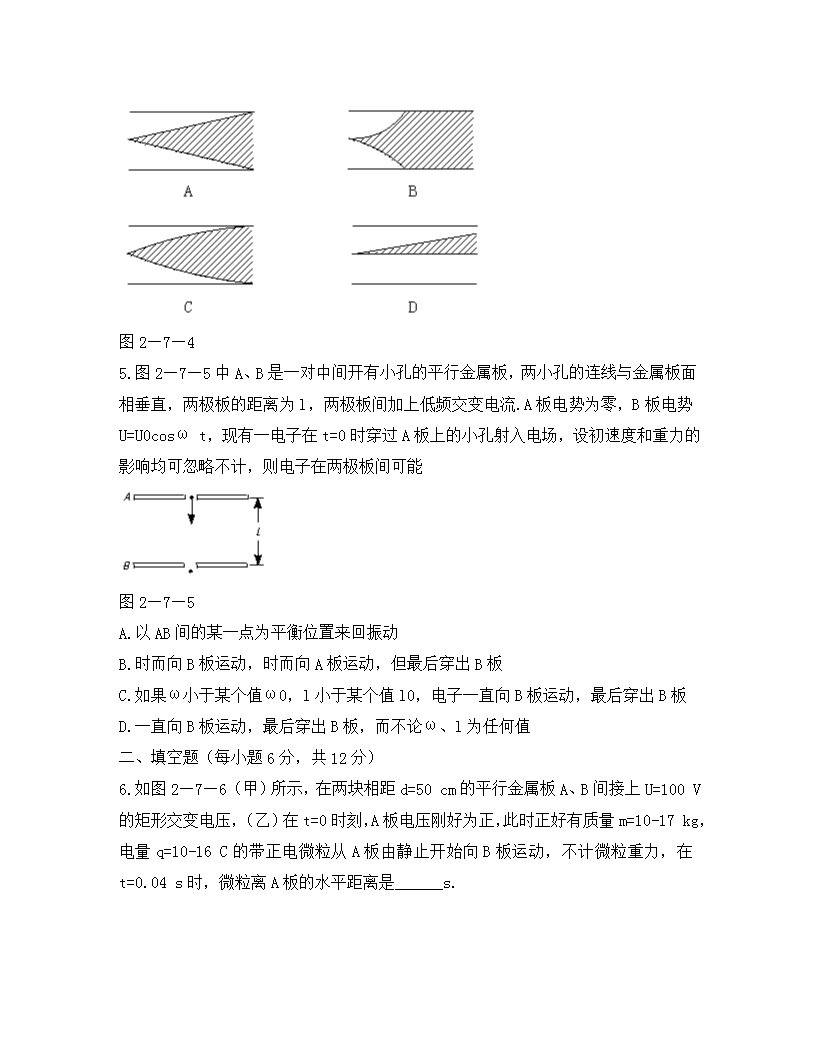4.一束电子射线以很大恒定速度v0射入平行板电容器两极板间，入射位置与两极板等距离，v0的方向与极板平面平行.今以交变电压U=Umsinω t加在这个平行板电容器上，则射入的电子将在两极板间的某一区域内出现.图2—7—4中的各图以阴影区表示这一区域，其中肯定不对的是 图2—7—4‎ ‎5.图2—7—5中A、B是一对中间开有小孔的平行金属板，两小孔的连线与金属板面相垂直，两极板的距离为l，两极板间加上低频交变电流.A板电势为零，B板电势U=U0cosω t，现有一电子在t=0时穿过A板上的小孔射入电场，设初速度和重力的影响均可忽略不计，则电子在两极板间可能 图2—7—5‎ A.以AB间的某一点为平衡位置来回振动 B.时而向B板运动，时而向A板运动，但最后穿出B板 C.如果ω小于某个值ω0，l小于某个值l0，电子一直向B板运动，最后穿出B板 D.一直向B板运动，最后穿出B板，而不论ω、l为任何值 二、填空题（每小题6分，共12分）‎ ‎6.如图2—7—6（甲）所示，在两块相距d=50 cm的平行金属板A、B间接上U=100 V的矩形交变电压，（乙）在t=0时刻，A板电压刚好为正，此时正好有质量m=10-17 kg，电量q=10-16 C的带正电微粒从A板由静止开始向B板运动，不计微粒重力，在t=0.04 s时，微粒离A板的水平距离是______s.‎ 图2—7—6‎ ‎7.如图2—7—7所示，水平放置的平行金属板下板小孔处有一静止的带电微粒，质量m，电量-q，两板间距6 mm，所加变化电场如图所示，若微粒所受电场力大小是其重力的2倍，要使它能到达上极板，则交变电场周期T至少为_______.‎ 图2—7—7‎ 三、计算题（共63分）‎ ‎8.（15分）N个长度逐个增大的金属圆筒和一个靶，沿轴线排成一串，如图2—7—8所示（图中只画出了6个圆筒做为示意）.各筒和靶相间的接到频率为f，最大电压为U的正弦交流电源的两端.整个装置放在真空容器中，圆筒的两底面中心开有小孔，有一质量为m，带电量为q的正离子沿轴线射入圆筒，并将在圆筒间及圆筒与靶间的缝隙处受到电场力的作用而加速（圆筒内都没有电场），缝隙的宽度很小，离子穿过缝隙的时间可以不计.已知离子进入第一个圆筒左端的速度为v1,且此时第一、二两个圆筒间的电势差φ1-φ2=-φ，为使打到靶上的离子获得最大能量，各个圆筒的长度应满足什么条件？并求出在这种情况下打到靶上的离子动能.‎ 图2—7—8‎ ‎9.（15分）如图2—7—9（甲）为平行板电容器，板长l=0.1 m，板距d=0.02 m.板间电压如图（乙）示，电子以v=1×107 m/s的速度，从两板中央与两板平行的方向射入两板间的匀强电场，为使电子从板边缘平行于板的方向射出，电子应从什么时刻打入板间？并求此交变电压的频率.(电子质量m=9.1×10-31 kg,电量e=1.6×10-19 C)‎ 图2—7—9‎ ‎10.(15分)如图2—7—10甲所示，A、B为两块距离很近的平行金属板，板中央均有小孔.一电子以初动能EkO=120 eV,从A板上的小孔O不断地垂直于板射入A、B之间，在B板的右侧，偏转板M、N组成一匀强电场，板长L=2×10-2 m，板间距离d=4×10-3 m；偏转板加电压为U2=20 V，现在A、B间加一个如图乙所示的变化电压U1，在t=2 s时间内，A板电势高于B板，则在U1随时间变化的第一周期内.‎ 图2—7—10‎ ‎(1)在哪段时间内，电子可从B板上小孔O′射出？‎ ‎(2)在哪段时间内，电子能从偏转电场右侧飞出？（由于A、B两板距离很近，可以认为电子穿过A、B所用时间很短，忽略不计）‎ ‎11.(18分）示波器是一种多功能电学仪器，可以在荧光屏上显示出被检测的电压波形.它的工作原理等效成下列情况：（如图2—7—11所示）真空室中电极K发出电子（初速不计），经过电压为U1的加速电场后，由小孔S沿水平金属板，A、B间的中心线射入板中.板长L，相距为d，在两板间加上如图乙所示的正弦交变电压，前半个周期内B板的电势高于A板的电势，电场全部集中在两板之间，且分布均匀.在每个电子通过极板的极短时间内，电场视作恒定的.在两极板右侧且与极板右端相距D处有一个与两板中心线垂直的荧光屏，中心线正好与屏上坐标原点相交.当第一个电子到达坐标原点O时，使屏以速度v沿-x方向运动，每经过一定的时间后，在一个极短时间内它又跳回到初始位置，然后重新做同样的匀速运动.(已知电子的质量为m，带电量为e，不计电子重力)求：‎ 图2—7—11‎ ‎（1）电子进入AB板时的初速度；‎ ‎（2）要使所有的电子都能打在荧光屏上，图乙中电压的最大值U0需满足什么条件？‎ ‎（3）要使荧光屏上始终显示一个完整的波形，荧光屏必须每隔多长时间回到初始位置？计算这个波形的最大峰值和长度.在如图2—7—11丙所示的x-y坐标系中画出这个波形.‎ 参考答案 一、1.BC 2.AB 3.BCD ‎4.ACD 不同时刻入射的电子在不同瞬时电压下，沿不同抛物线做类平抛运动，其轨迹符合方程y= x2(U为变化电压），x轴正向为初速v0方向，y轴的正方向垂直于初速v0向上或向下.电压低时从板间射出，电压高时打在板上，电子在板间出现的区域边界应为开口沿纵坐标方向的抛物线.‎ ‎5.AC 二、6.0.4 m 7. 6.0×10-2 s 三、8.由于金属筒对电场的屏蔽作用，使离子进入筒后做匀速直线运动，只有当离子到达两筒的缝隙处才能被加速.这样离子在筒内运动时间为t= (T、f分别为交变电压周期、频率)①，设离子到第1个筒左端速度为v1，到第n个筒左端速度vn，第n个筒长为Ln，则Ln=vn·t ②‎ 从速度v1加速vn经过了（n-1）次加速，由功能关系有：mvn2=mv12+(n-1)·qU ③‎ 联立得Ln=‎ Ekn==mv12+(n-1)qU 令n=N,则得打到靶上离子的最大动能mvN2=mv12+(N-1)qU ‎9.电子水平方向匀速直线运动，竖直方向做变加速运动.要使电子从板边平行于板方向飞出，则要求电子在离开板时竖直方向分速度为0，并且电子在竖直方向应做单向直线运动向极板靠近.此时电子水平方向（x方向）、竖直方向（y）方向的速度图线分别如图所示 . 电子须从t=n (n=0,1，2,…)时刻射入板间，且穿越电场时间t=kT(k=1,2…)①,而电子水平位移l=vt②‎ 竖直位移d=·2k ③‎ 三式联立得，T==2.5×10-9 s,k=4,故f=1/T=4×108 Hz,且k=4.‎ ‎10.（1）0~2 s电子能从O′射出，动能必须足够大，由功能关系得U1e＜Ek0得U1＜120 V 所以当t＜0.6或t＞1.4时，粒子可由B板小孔O′射出.‎ ‎（2）电子进入偏转极板时的水平速度为v,通过偏转电极时，侧向偏移是y,‎ y=‎ 能从偏转电场右侧飞出的条件是y＜得mv2＞‎ 代入数字的mv2＞250 eV,即AB间必须有130 V的加速电压，所以当2.65 s＜t＜3.35 s时，电子能从偏转电场右侧飞出，如图所示.‎ ‎11.（1）电子在加速电场中运动，据动能定理，有 eU1=mv12,v1=‎ ‎(2)因为每个电子在板A、B间运动时，电场均匀、恒定，故电子在板A、B间做类平抛运动，在两板之外做匀速直线运动打在屏上.在板A、B间沿水平方向运动时，有 ‎ ‎ L=v1t,‎ 竖直方向，有 y′=at2,且a=，‎ 联立解得 y′=.‎ 只要偏转电压最大时的电子能飞出极板打在屏上，则所有电子都能打在屏上，所以 ym′=＜,U0＜.‎ ‎(3)要保持一个完整波形，需每隔周期T回到初始位置，设某个电子运动轨迹如图所示，有 tanθ=,又知 y′=，联立得 L′=.‎ 由相似三角形的性质，得,‎ ‎ 则 y=,‎ 峰值为 ym=.‎ 波形长度为 x1=vT.‎ 波形如图所示. ‎