高中物理第二章匀变速直线运动的研究章末总结讲基础版含解析新人教版必修 14页

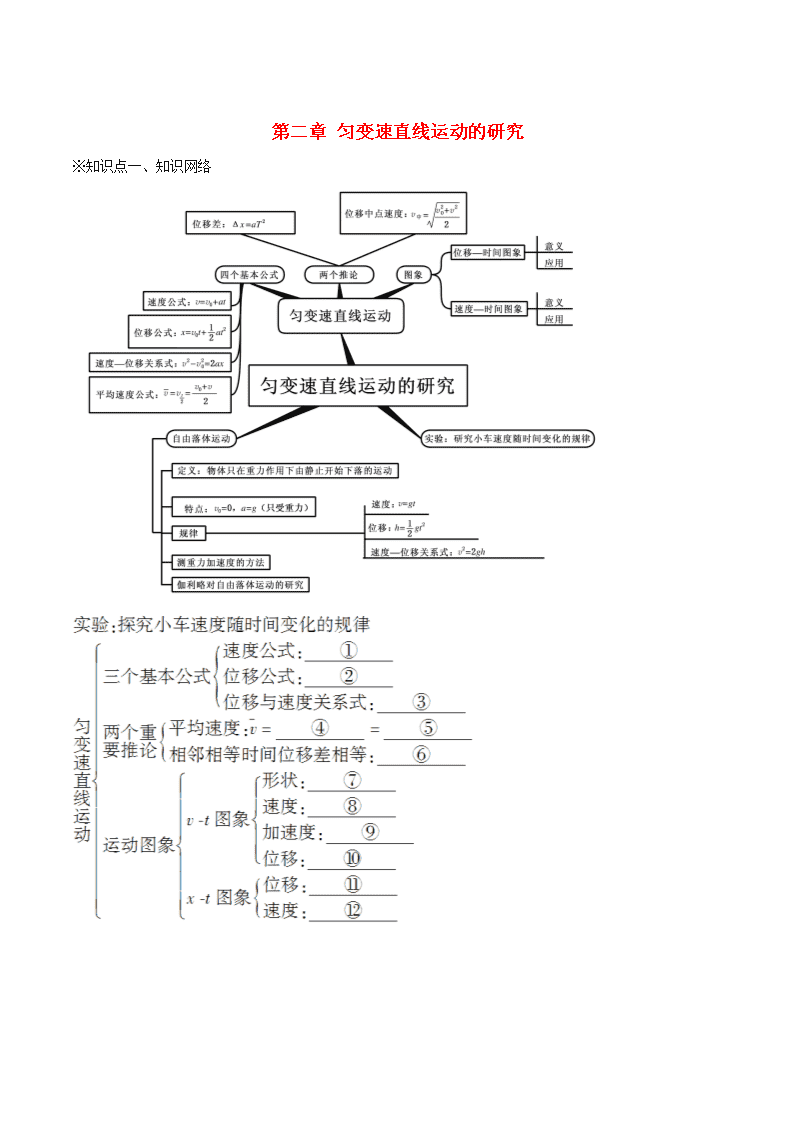
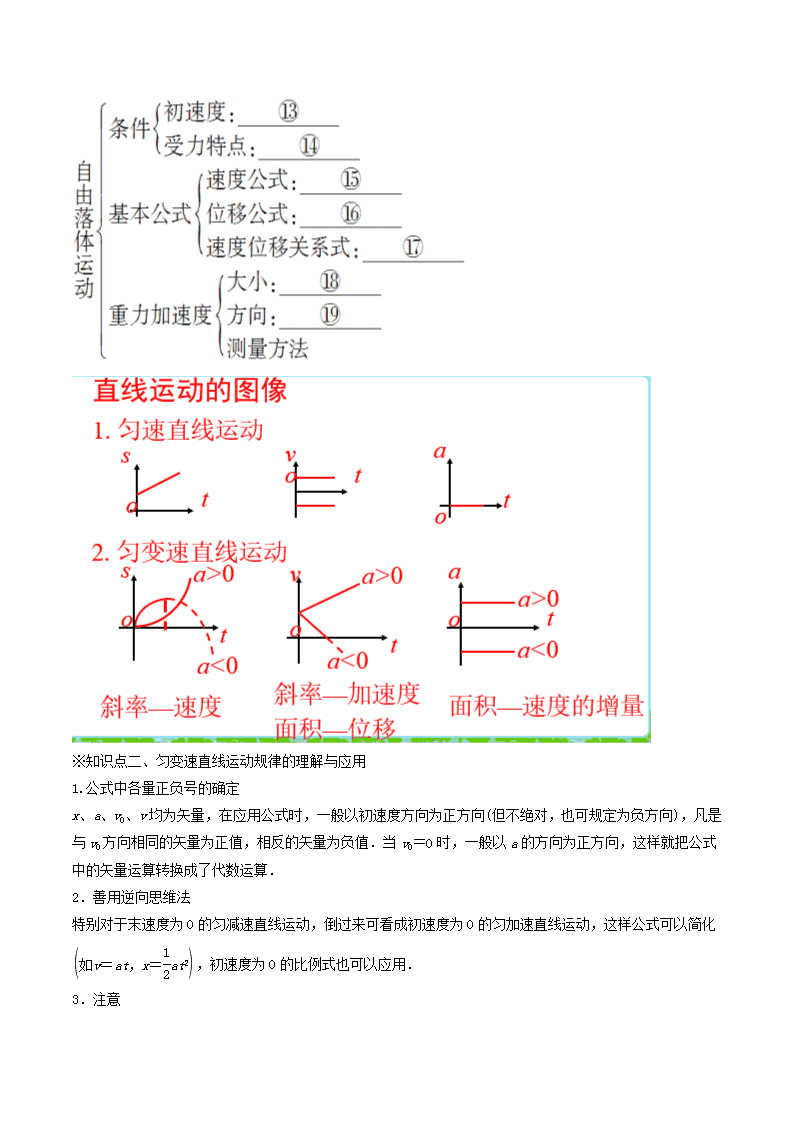
第二章 匀变速直线运动的研究 ※知识点一、知识网络 ※知识点二、匀变速直线运动规律的理解与应用 1.公式中各量正负号的确定 x、a、v0、v 均为矢量，在应用公式时，一般以初速度方向为正方向(但不绝对，也可规定为负方向)，凡是 与 v0 方向相同的矢量为正值，相反的矢量为负值．当 v0＝0 时，一般以 a 的方向为正方向，这样就把公式中 的矢量运算转换成了代数运算． 2．善用逆向思维法 特别对于末速度为 0 的匀减速直线运动，倒过来可看成初速度为 0 的匀加速直线运动，这样公式可以简化 如 v＝at，x＝1 2 at2 ，初速度为 0 的比例式也可以应用． 3．注意 (1)解题时首先选择正方向，一般以 v0 方向为正方向． (2)刹车类问题一般先求出刹车时间． (3)对于有往返的匀变速直线运动(全过程加速度 a 恒定)，可对全过程应用公式 v＝v0＋at、x＝v0t＋ 1 2 at2、……列式求解． (4)分析题意时要养成画运动过程示意图的习惯，特别是对多过程问题．对于多过程问题，要注意前后过程 的联系——前段过程的末速度是后一过程的初速度；再要注意寻找位移关系、时间关系. 4．匀变速直线运动 的常用解题方法 【典型例题】 【例题 1】一个物体以 v0＝8m/s 的初速度沿光滑斜面向上滑，加速度的大小为 2 m/s2，冲上最高点之后， 又以相同的加速度往回运动，下列说法错误的是( ) A．1 s 末的速度大小为 6 m/s B．3 s 末的速度为零 C．2 s 内的位移大小是 12 m D．5 s 内的位移大小是 15 m 【审题指导】分析题中已知条件选择合适的关系式求解． 【答案】 B 【针对训练】在某地地震发生后的几天，通向灾区的公路非常难行，一辆救灾汽车由静止开始做匀变速直 线运动，刚运动了 8 s，由于前方突然有巨石滚在路中央，所以又紧急刹车，经 4 s 停在巨石前．则关于汽 车的运动情况，下列说法正确的是 ( ) A．加速、减速中的加速度大小之比 a1∶a2＝1∶2 B．加速、减速中的加速度大小之比 a1∶a2＝2∶1 C．加速、减速中的平均速度之比 v－ 1∶ v－ 2＝2∶1 D．加速、减速中的位移之比 x1∶x2＝1∶1 【答案】A 【解析】 由 a＝v－v0 t 可得 a1∶a2＝1∶2，选项 A 正确，B 错误；由 v－＝v0＋v 2 可得 v－∶ v－ 2＝1∶1，选项 C 错误；又根据 x＝ v－t，x1∶x2＝2∶1，选项 D 错误． ※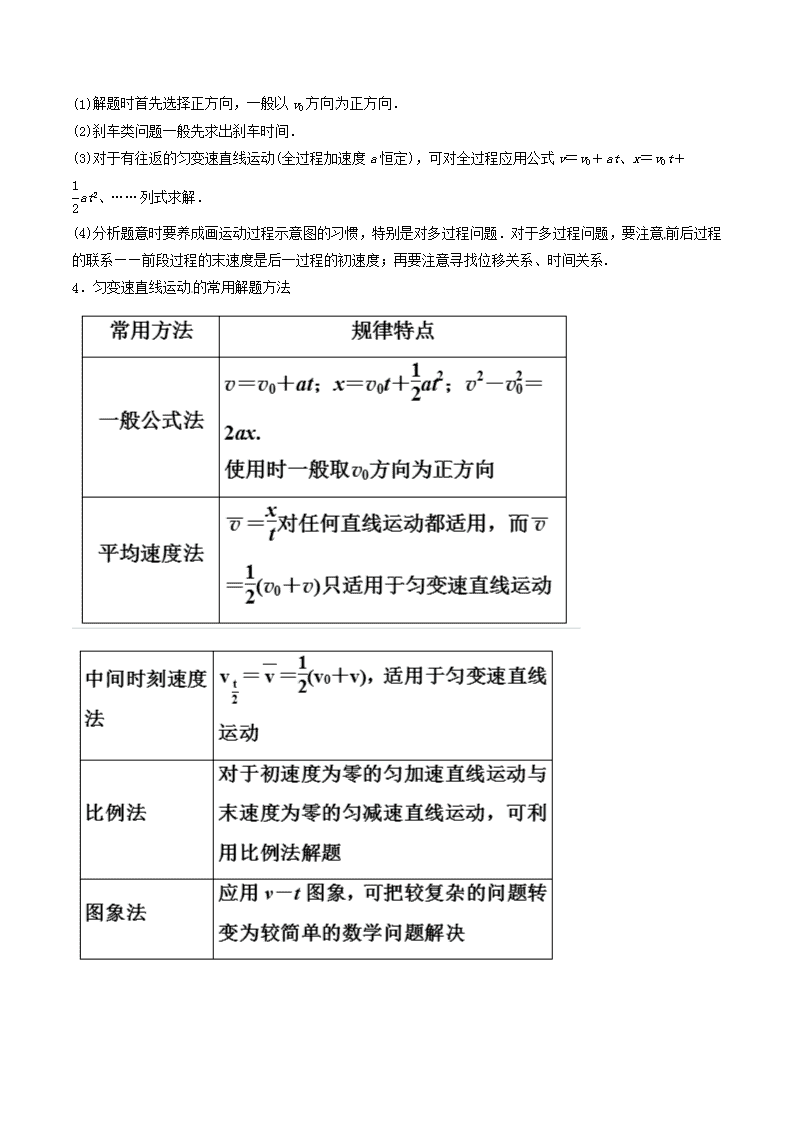知识点三、x-t 图象和 v-t 图象 ★x－t 图象和 v－t 图象的比较 2.在图象问题的学习与应用中首先要注意区分它们的类型，其次应从图象所表达的物理意义，图象的斜率、 截距、交点、拐点、面积等方面的含义加以深刻理解． 【典型例题】 【例题 2】在水平直轨道上距离 A 点右侧 10 m 处，一辆小车以 4 m/s 的速度匀速向右行驶，5 s 末，小车 的速度立即变为 2 m/s 匀速向左行驶．设小车做直线运动的位移和运动方向都以水平向左为正方向， (1)试作出小车在 20 s 内的 v－t 图象和 x－t 图象：(写出必要的计算过程，以小车出发点为位移坐标原点)； (如图所示) (2)根据图象确定小车在 20 s 末的位置．(用文字表达) 【针对训练】一质点由静止开始做直线运动的 v－t 关系图象如图所示，则该质点的 x－t 关系图象可大致 表示为下图中的( ) 【答案】 B ※知识点四、纸带问题的处理方法 纸带的分析与计算是近几年高考中考查的热点，因此应该掌握有关纸带问题的处理方法． 1．判断物体的运动性质 (1)根据匀速直线运动的位移公式 x＝vt 知，若纸带上各相邻的点的间隔相等，则可判定物体做匀速直线运 动． (2)由匀变速直线运动的推论Δx＝aT2 知，若所打的纸带上在任意两个相邻且相等的时间内物体的位移差相 等，则说明物体做匀变速直线运动． 2．求瞬时速度 根据在匀变速直线运动中，某段时间内的平均速度等于该段时间中间时刻的瞬时速度：vn＝xn＋xn＋1 2T ，即 n 点的瞬时速度等于(n－1)点和(n＋1)点间的平均速度． 3．求加速度 (1)逐差法 虽然用 a＝Δx T2 可以根据纸带求加速度，但只利用一个Δx 时，偶然误差太大，为此应采取逐差法． 如图所示，纸带上有六个连续相等的时间间隔 T 内的位移 x1、x2、x3、x4、x5、x6.由Δx＝aT2 可得： x4－x1＝(x4－x3)＋(x3－x2)＋(x2－x1)＝3aT2 x5－x2＝(x5－x4)＋(x4－x3)＋(x3－x2)＝3aT2 x 6－x3＝(x6－x5)＋(x5－x4)＋(x4－x3)＝3aT2 所以 a＝（x6－x3）＋（x5－x2）＋（x4－x1） 9T2 ＝（x6＋x5＋x4）－（x3＋x2＋x1） 9T2 . (2)两段法 将如图所示的纸带分为 OC 和 CF 两大段，每段时间间隔是 3T，可得：x4＋x5＋x6－(x1＋x2＋x3)＝a(3T)2，显 然，求得的 a 和用逐差法所得的结果是一样的，但该方法比逐差法简单多了． (3)v－t 图象法 根据纸带，求出各时刻的瞬时速度，作出 v－t 图象，求出该 v－t 图象的斜率 k，则 k＝a. 这种方法的优点是可以舍掉一些偶然误差较大的测量值，有效地减少偶然误差． 【典型例题】 【例题 3】某兴趣小组利用自由落体运动测定重力加速度，实验装置如图所示．倾斜的球槽中放有若干个小 铁球，闭合开关 K，电磁铁吸住第 1 个小球．手动敲击弹性金属片 M，M 与触头瞬间分开，第 1 个小球开始 下落，M 迅速恢复，电磁铁又吸住第 2 个小球．当第 1 个小球撞击 M 时，M 与触头分开，第 2 个小球开始下 落…….这样，就可测出多个小球下落的总时间． (1)在实验中，下列做法正确的是________． A．电路中的电源只能选用交流电源 B．实验前应将 M 调整到电磁铁的正下方 C．用直尺测量电磁铁下端到 M 的竖直距离作为小球下落的高度 D．手动敲击 M 的同时按下秒表开始计时 (2)实验测得小球下落的高度 H＝1.980 m,10 个小球下落的总时间 T＝6.5 s．可求出重力加速度 g＝________ m/s2.(结果保留两位有效数字) (3)某同学考虑到电磁铁在每次断电后需要时间△t 磁性才消失，因此，每个小球的实际下落时间与它的测 量时间相差△t，这导致实验误差．为此，他分别取高度 H1 和 H2 测量n 个小球下落的总时间 T1 和 T2.他是否 可以利用这两组数据消除△t 对实验结果的影响？________(填“是”或“否”) (4)在不增加实验器材的情况下，请提出减小实验误差的两个办法． ①________________________________________________________________________； ②________________________________________________________________________. 【答案】 (1)BD (2)9.4 (3)是 (4)见解析 (2)H＝1 2 gt2＝1 2 g T 10 2 所以 g＝200H T2 ＝200×1.980 (6.5 )2 m/s2＝9.4 m/s2 (3)由 H1＝1 2 g T1 n －Δt 2 和 H2＝1 2 g T2 n －Δt 2 可得 g＝2n2( H1－ H2)2 (T1－T2)2 ，因此可以消去Δt 的影响． (4)增加小球下落的高度或多次重复实验，取平均值做为最后的测量结果均能使实验误差减小 【针对训练】 在做“探究小车速度随时间变化的规律”的实验中，取一段如图所示的纸带研究其运动情 况．设 O 点为计数的起始点，在四个连续的计数点中，相邻计数点间的时间间隔为 0.1 s，若物体做理想的 匀加速直线运动，则计数点“A”与起始点 O 之间的距离 x1 为________ cm，打计数点“A”时物体的瞬时速 度为________ m/s，物体的加速度为________ m/s2. 【答案】 4.00 0.50 2.00 【解析】 设相邻相等时间内的位移之差为Δx，则 AB ＝x1＋Δx，BC ＝x1＋2Δx，OC ＝ OA ＋ AB ＋ BC ＝3(x1＋Δx)＝18.00 cm，故 AB ＝6.00 cm，x1＝4.00 cm；由Δx＝aT2＝2.00 cm 可得 a＝2.00 m/s2；A 点 的速度 vA＝ OA ＋ AB 2T ＝0.50 m/s. ※知识点五、追及相遇问题 ★追及问题的解题思路： (1)根据对两物体运动过程的分析，画出两物体运动的示意图． (2)根据两物体的运动性质，分别列出物体的位移方程，注意要将两物体运动时间的关系反映在方程中． (3)由运动示意图找出两物体位移间的关联方程，这是关键． (4)联立方程求解，并对结果进行简单分析． 【典型例题】 【例题4】A 火车以v1=20m/s 速度匀速行驶，司机发现前方同轨道上相距100m处有另一列火车B正以v2=10m/s 速度匀速行驶，A 车立即做加速度大小为 a 的匀减速直线运动。要使两车不相撞，a 应满足什么条件？ 【针对训练】甲车以加速度 3 m/s2 由静止开始做匀加速直线运动．乙车落后 2 s 在同一地点由静止开始， 以加速度 6 m/s2 做匀加速直线运动．两车的运动方向相同，求： (1)在乙车追上甲车之前，两车距离的最大值是多少？ (2)乙车出发后经多长时间可追上甲车？此时它们离出发点多远？ (2)设乙车出发后经 t′秒追上甲车，则 x1＝1 2 a 甲(t′＋2)2＝1 2 ×3×(t′＋2)2 m， x2＝1 2 a 乙 t′2＝1 2 ×6×t′2m 由 x1＝x2 代入数据， 求得 t′＝(2＋2 2)s. 将所求得时间代入位移公式可得 x1＝x2≈70 m. 【答案】 (1)12 m (2)(2＋2 2) s 70 m