【物理】2018届二轮复习 　电场和磁场 学案（全国通用） 11页

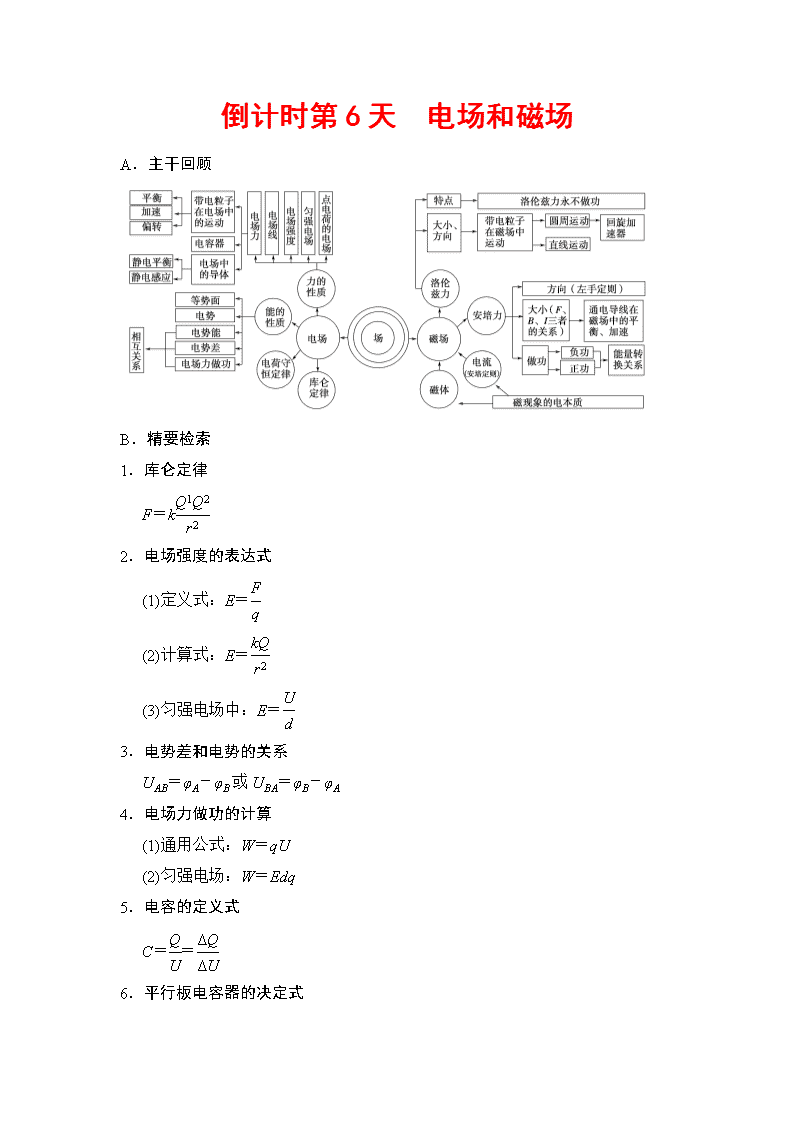
倒计时第6天　电场和磁场 A．主干回顾 B．精要检索 ‎1．库仑定律 F＝k ‎2．电场强度的表达式 ‎(1)定义式：E＝ ‎(2)计算式：E＝ ‎(3)匀强电场中：E＝ ‎3．电势差和电势的关系 UAB＝φA－φB或UBA＝φB－φA ‎4．电场力做功的计算 ‎(1)通用公式：W＝qU ‎(2)匀强电场：W＝Edq ‎5．电容的定义式 C＝＝ ‎6．平行板电容器的决定式 C＝ ‎7．磁感应强度的定义式 B＝ ‎8．安培力大小 F＝BIL(B、I、L相互垂直)‎ ‎9．洛伦兹力的大小 F＝qvB ‎10．带电粒子在匀强磁场中的运动 ‎(1)洛伦兹力充当向心力，‎ qvB＝mrω2＝m＝mr＝4π2mrf2＝ma．‎ ‎(2)圆周运动的半径r＝、周期T＝．‎ ‎11．速度选择器 如图1所示，当带电粒子进入电场和磁场共存的空间时，同时受到电场力和洛伦兹力作用，F电＝Eq，F洛＝Bqv0，若Eq＝Bqv0，有v0＝，即能从S2孔飞出的粒子只有一种速度，而与粒子的质量、电性、电量无关．‎ 图1‎ ‎12．电磁流量计 如图2所示，一圆形导管直径为d，用非磁性材料制成，其中有可以导电的液体向左流动，导电流体中的自由电荷(正、负离子)在洛伦兹力作用下横向偏转，a、b间出现电势差．当自由电荷所受电场力和洛伦兹力平衡时，a、b间的电势差就保持稳定．‎ 由qvB＝qE＝q 可得v＝ 流量Q＝Sv＝·＝．‎ 图2‎ ‎13．磁流体发电机 如图3是磁流体发电机，等离子气体喷入磁场，正、负离子在洛伦兹力作用下发生上下偏转而聚集到A、B板上，产生电势差，设A、B平行金属板的面积为S，相距为L，等离子气体的电阻率为ρ，喷入气体速度为v，板间磁场的磁感应强度为B，板外电阻为R，当等离子气体匀速通过A、B板间时，板间电势差最大，离子受力平衡：qE场＝qvB，E场＝vB，电动势E＝E场L＝BLv，电 内电阻r＝ρ，故R中的电流I＝＝＝．‎ 图3‎ ‎14．霍尔效应 如图4所示，厚度为h，宽度为d的导体板放在垂直于磁感应强度为B的匀强磁场中，当电流流过导体板时，在导体板上下侧面间会产生电势差，U＝k(k为霍尔系数)．‎ 图4‎ ‎15．回旋加速器 如图5所示，是两个D形金属盒之间留有一个很小的缝隙，有很强的磁场垂直穿过D形金属盒．D形金属盒缝隙中存在交变的电场．带电粒子在缝隙的电场中被加速，然后进入磁场做半圆周运动．‎ 图5‎ ‎(1)粒子在磁场中运动一周，被加速两次；交变电场的频率与粒子在磁场中圆周运动的频率相同．‎ T电场＝T回旋＝T＝．‎ ‎(2)粒子在电场中每加速一次，都有qU＝ΔEk．‎ ‎(3)粒子在边界射出时，都有相同的圆周半径R，有R＝．‎ ‎(4)粒子飞出加速器时的动能为Ek＝＝．在粒子质量、电量确定的情况下，粒子所能达到的最大动能只与加速器的半径R和磁感应强度B有关，与加速电压无关．‎ ‎16．带电粒子在电场中偏转的处理方法 ‎17．带电粒子在有界磁场中运动的处理方法 ‎(1)画圆弧、定半径：‎ 从磁场的边界点、或轨迹与磁场边界的“相切点”等临界点入手；充分应用圆周运动相互垂直的“速度线”与“半径线”．‎ 图6‎ ‎①过粒子运动轨迹上任意两点M、N(一般是边界点，即“入射点”与“出射点”)，作与速度方向垂直的半径，两条半径的交点是圆心O，如图6甲所示．‎ ‎②过粒子运动轨迹上某一点M(一般是“入射点”或“出射点”)，作与速度方向垂直的直线，再作M、N两点连线(弦)的中垂线，其交点是圆弧轨道的圆心O，如图乙所示．‎ ‎(2)确定几何关系： ‎ 在确定圆弧、半径的几何图形中，作合适辅助线，依据圆、三角形的特点，应用勾股定理、三角函数、三角形相似等，写出运动轨迹半径r、圆心角(偏向角)θ、与磁场的宽度、角度、相关弦长等的几何表达式．‎ ‎(3)确定物理关系： ‎ 相关物理关系式主要为半径r＝，粒子在磁场的运动时间t＝T＝T(圆弧的圆心角φ越大，所用时间越长，与半径大小无关)，周期T＝．‎ C．考前热身 ‎1．两个等量同种点电荷固定于光滑水平面上，其连线中垂线上有A、B、C三点，如图7甲所示．一个电荷量为‎2 C，质量为‎1 kg的小物块从C点由静止释放，其运动的vt图象如图7乙所示，其中B点处为整条图线切线斜率最大的位置(图中标出了该切线)．则下列说法正确的是(　　) ‎ ‎【导 号：17214226】‎ 图7‎ A．B点为中垂线上电场强度最大的点，电场强度E＝2 V/m B．物块由C到A的过程中，电势能先减小后变大 C．由C点到A点的过程中，各点电势逐渐升高 D．A、B两点的电势差UAB＝－5 V D　[读取vt图象信息．B点的斜率为此时的加速度为‎2 m/s2，为最大值，则电场力为最大值F＝ma＝2 N，则电场强度最大值为E＝＝1 N/C，故A错误．‎ C到A的过程中，物块速度增大，则电场力做正功，电势能减小，故B错误．‎ 理解等量同种点电荷电场的几何形状，电荷连线中垂线上的电场强度的方向由O点沿中垂线指向外侧， 则由C点到A点的过程中电势逐渐减小，故C错误．‎ A、B两点的速度分别为‎6 m/s、‎4 m/s，由动能定理得电场力做功为WBA＝mv－mv＝10 J，则电势差为UAB＝＝＝－5 V，故D正确．]‎ ‎2．(多选)如图8所示，平行金属板AB之间接恒定电压，一重力不计的带正电粒子自A板附近由静止释放，粒子匀加速向B板运动．则下列说法正确的是(　　)‎ 图8‎ A．若开关S保持闭合，减小AB间的距离，则粒子到达B板的速度将增大 B．若开关S保持闭合，减小AB间的距离，运动时间将减小 C．若断开S，减小AB间的距离，则粒子到达B板的速度将增大 D．若断开S，减小AB间的距离，运动时间将减小 BD　[开关S保持闭合时，AB两板间电压U保持不变．由v＝得速度v不变．由d＝vt知若d减小，则t减小，故A错误，B正确．断开S时，AB两板带电荷量不变，所以当减小AB间的距离d时，板间电场强度E不变，则粒子的加速度不变．由v＝得v减小．由d＝at2知若d减小，a不变，则t减小，故C错误，D正确．]‎ ‎3．(多选)一个负离子，质量为m，带电荷量大小为q，以速率v垂直于屏S经过小孔O射入存在着匀强磁场的真空室中，如图9所示．磁感应强度B的方向与离子的运动方向垂直，并垂直于图中纸面向里 (　　)‎ ‎【导 号：17214227】‎ 图9‎ A．离子进入磁场后到达屏S上时的位置与O点的距离为 B．离子进入磁场后到达屏S上时的位置与O点的距离为 C．离子进入磁场后经过时间t到达位置P，则有θ＝t D．离子进入磁场后经过时间t到达位置P，则有θ＝t BD　[由题图知，OQ是半径，由qvB＝得r＝，所以到达屏S的位置与O点的距离为2r＝，故A错误，B正确；由几何关系得圆心角为2θ，所以t＝T＝，可得θ＝，故C错误，D正确．]‎ ‎4．如图10，虚线所示的圆形区域内存在一垂直于纸面的匀强磁场，P为磁场边界上的一点，大量相同的带电粒子以相同的速率经过P 点，在纸面内沿不同方向射入磁场，若粒子射入的速率为v1，这些粒子在磁场边界的出射点分布在六分之一圆周上；若粒子射入速率为v2，相应的出射点分布在三分之一圆周上，不计重力及带电粒子之间的相互作用，则v2∶v1为(　　)‎ 图10‎ A．∶2　　　　　　　　　 B．∶1‎ C．∶1 D．3∶ C　[设圆形区域磁场的半径为r，当速度大小为v1时，从P点入射的粒子射出磁场时与磁场边界的最远交点为M(图甲)时，由题意知∠POM＝60°，由几何关系得轨迹圆半径为R1＝；‎ 当速度大小为v2时，从P点入射的粒子射出磁场时与磁场边界的最远交点为N(图乙)；由题意知∠PON＝120°，由几何关系得轨迹圆的半径为R2＝r；根据洛伦兹力充当向心力可知：Bqv＝m，解得：v＝，故速度与半径成正比，因此v2∶v1＝R2∶R1＝∶1，故C正确，A、B、D错误．]‎ 甲　　　　　　　乙 ‎5．如图11所示，在直角坐标系xOy平面内有一矩形区域MNPQ，矩形区域内有水平向右的匀强电场，场强为E；在y≥0的区域内有垂直于坐标平面向里的匀强磁场，半径为R的光滑绝缘空心半圆管ADO固定在坐标平面内，半圆管的一半处于电场中，圆心O1为MN的中点，直径AO垂直于水平虚线MN，一质量为m、电荷量为q的带电粒子(重力不计)从半圆管的O点由静止释放，进入管内后从A点穿出恰能在磁场中做半径为R的匀速圆周运动，当粒子再次进入矩形区域MNPQ时立即撤去磁场，此后粒子恰好从QP的中点C 离开电场．求：‎ 图11‎ ‎(1)匀强磁场的磁感应强度B的大小；‎ ‎(2)矩形区域的长度MN和宽度MQ应满足的条件．‎ ‎(3)粒子从A点运动到C点的时间．‎ ‎【解析】　(1)粒子从O到A过程中由动能定理得：qER＝mv2‎ 从A点穿出后做匀速圆周运动，有：qvB＝m 解得：B＝．‎ ‎(2)粒子再次进入矩形区域后做类平抛运动，由题意得：R＝at2‎ a＝ R＋OC＝vt 联立解得：OC＝R 所以，矩形区域的长度MN≥2R，宽度MQ＝2R．‎ ‎(3)粒子从A点到矩形边界MN的过程中，‎ 有：t1＝＝ 从矩形边界MN到C点的过程中，有：t2＝＝ 故所求时间为：t总＝t1＋t2＝．‎ ‎【答案】　(1) ‎(2)矩形区域的长度MN≥2R，宽度MQ＝2R ‎(3) ‎6．如图12所示，在直角坐标系xOy平面内，虚线MN平行于y轴，N点坐标(－l，0)，MN与y轴之间有沿y轴正方向的匀强电场，在第四象限的某区域有方向垂直于坐标平面的圆形有界匀强磁场(图中未画出)．现有一质量为m、电荷量大小为e的电子，从虚线MN上的P点， 以平行于x轴正方向的初速度v0射入电场，并从y轴上A点(0，0．‎5l)射出电场，射出时速度方向与y轴负方向成30°角，以后，电子做匀速直线运动，进入磁场并从圆形有界磁场边界上Q点射出，速度沿x轴负方向．不计电子重力．求：‎ 图12‎ ‎(1)匀强电场的电场强度E的大小？‎ ‎(2)匀强磁场的磁感应强度B的大小？电子在磁场中运动的时间t是多少？‎ ‎(3)圆形有界匀强磁场区域的最小面积S是多大？ ‎ ‎【导 号：17214228】‎ ‎【解析】　(1)设电子在电场中运动的加速度为a，时间为t，离开电场时，沿y轴方向的速度大小为vy， 则 a＝ vy＝at l＝v0t vy＝v0cot 30°‎ 解得：E＝．‎ ‎(2)设轨迹与x轴的交点为D，OD距离为xD，‎ 则xD＝0．5ltan 30°＝ 所以DQ平行于y轴，电子在磁场中做匀速圆周运动的轨道的圆心在DQ上，电子运动轨迹如图所示．‎ 设电子离开电场时速度为v，在磁场中做匀速圆周运动的轨道半径为r，则 v0＝vsin 30°‎ r＝＝ r＋＝l t＝T T＝ 解得：B＝，t＝．‎ ‎(3)以切点F、Q为直径的圆形有界匀强磁场区域的半径最小，设为r1，则r1＝rcos 30°＝＝ S＝πr＝．‎ ‎【答案】　(1)　(2)　　(3)