2018届二轮复习　万有引力与航天课件（37张）全国通用 37页

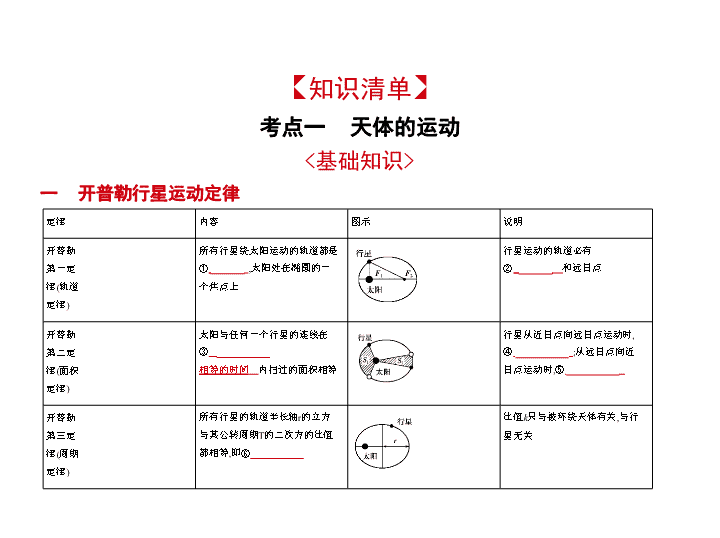
一    开普勒行星运动定律 定律 内容 图示 说明 开普勒 第一定 律(轨道 定律) 所有行星绕太阳运动的轨道都是 ① 　椭圆     ,太阳处在椭圆的一 个焦点上   行星运动的轨道必有 ② 　近日点     和远日点 开普勒 第二定 律(面积 定律) 太阳与任何一个行星的连线在 ③ 　相等的时间     内扫过的面积相等   行星从近日点向远日点运动时, ④ 　速率变小     ;从远日点向近 日点运动时,⑤ 　速率变大     开普勒 第三定 律(周期 定律) 所有行星的轨道半长轴r的立方 与其公转周期T的二次方的比值 都相等,即⑥      r 3 / T 2 = k        比值 k 只与被环绕天体有关,与行 星无关 考点一    天体的运动 < 基础知识 > 知识清单 内容 自然界中任何两个物体都相互吸引,引力的方向在它们的连线上,引力的大小F与物体的质 量m 1 和m 2 的乘积⑦ 　成正比     ,与它们之间距离r的平方⑧ 　成反比     公式 F=G   ,引力常量G=6.67 × 10 -11 N · m 2 / kg 2 适用条件 (1)两质点间的作用 (2)可视为质点的物体间的作用 (3)质量分布均匀的球体间的作用 万有引力的特性 普遍性 任何有质量的客观存在的物体间都有这种引力 相互性 满足牛顿第三定律 宏观性 通常情况下万有引力非常小,只有在质量巨大的星体间或其附近空间才有意义 确定性 两物体间的万有引力只与它们本身的质量和距离有关,而与物体所在空间的性质、是否受到其他外力等无关 二    万有引力定律 三　 引力常量 数值 6.67 × 10 -11 N · m 2 / kg 2 测定人 英国物理学家卡文迪许 物理 意义 数值上等于两个质量都是⑨     1 kg     的物体相距⑩     1 m     时的相互 引力 测定 意义 (1)有力地证明了   　万有引力     的存在 (2)使定量计算得以实现 (3)开创了测量弱相互作用的新时代 实验装置   P :石英丝     M :平面镜     O :光源     N :刻度尺     Q :倒立T形架 实验思想 主要思想:放大 (1)利用四个球间引力 (2)利用T形架的转动即利用力矩增大引力的可观察效果 (3)利用小平面镜对光的反射来增大可测量的扭转角度 一、重力的理解 重力是地面附近的物体受到地球的万有引力而产生的;万有引力是物体 随地球自转所需向心力和重力的合力。 < 重点难点 > 如图所示,F 引 产生两个效果:一是提供物体随地球自转所需的向心力;二 是产生物体的重力。由于F 向 =mω 2 r,随纬度的增大而减小,所以物体的重 力随纬度的增大而增大,即重力加速度从赤道到两极逐渐增大。但F 向 一般很小,在一般情况下可认为重力和万有引力近似相等,即G   =mg, g=G   常用来计算星球表面的重力加速度。 在地球同一纬度处,重力加速度随物体离地面高度的增加而减小,因为 物体所受万有引力随物体离地面高度的增加而减小,即g'=G   。 说明 　g=G   和g'=G   不仅适用于地球,也适用于其他星球。 在赤道处,物体所受的万有引力F 引 分解的两个分力F 向 和mg刚好在一条 直线上,则有F 引 =F 向 +mg。 例1 　已知质量分布均匀的球壳对壳内物体的引力为0。假设地球是一 半径为R的质量分布均匀的球体,地球表面的重力加速度大小为g。试 求: (1)在地面上方离地面距离为   处的重力加速度大小与在地面下方地球 内部离地面距离为   处的重力加速度大小之比为多少? (2)设想地球的密度不变,自转周期不变,但地球球体半径变为原来的一 半,仅考虑地球和同步卫星之间的相互作用力,则该“设想地球”的同 步卫星的轨道半径与以前地球的同步卫星的轨道半径的比值是多少?   解析 　(1)由万有引力等于重力知   =mg 1   =mg 2 且有   =   =   则   =   (2)地球对同步卫星的万有引力提供同步卫星转动的向心力   =m'   r 1   =m'   r 2 M=ρ·   π R 3 M 1 =ρ·   π   解得   =     答案 　(1)8∶9　(2)   二、天体的质量、密度 通过观察绕天体做匀速圆周运动的卫星的周期T、半径r,由万有引力等 于向心力即G   =m   ·r,得 天体质量M=   。 (1)若知道天体的半径R,则天体的密度 ρ=   =   =   。 (2)若天体的卫星环绕天体表面运动,其轨道半径r等于天体半径R,其周 期为T,则天体密度ρ=   。 例2     (2017河南六市一模,18)随着地球资源的枯竭和空气污染如雾霾 的加重,星球移民也许是最好的方案之一。美国 NASA 于2016年发现一 颗迄今为止与地球最类似的太阳系外的行星,与地球的相似度为0.98,并 且可能拥有大气层和流动的水,这颗行星距离地球约1400光年,公转周 期约为37年,这颗名叫 Kepler 452 b 的行星,它的半径大约是地球的1.6倍, 重力加速度与地球的相近。已知地球的第一宇宙速度为7.9 km / s ,则下 列说法正确的是   (　　) A.飞船在 Kepler 452 b 表面附近运行时的速度小于7.9 km / s B.该行星的质量约为地球质量的1.6倍 C.该行星的平均密度约是地球平均密度的   D.在地球上发射航天器到达该星球,航天器的发射速度至少要达到第三 宇宙速度   解析     飞船在该行星表面附近运行时的速度v K =   =   >   =7.9 km / s , A 项错误。由   =mg,得M=   ,则   =   =1.6 2 ,则 M K =1.6 2 M 地 =2.56M 地 , B 项错误。由ρ=   ,V=   π R 3 ,M=   ,得ρ=   ,则   =   =   , C 项正确。因为该行星在太阳系之外,则在地球上发射航天 器到达该星球,航天器的发射速度至少要达到第三宇宙速度, D 项正确。   答案     CD 一    三个宇宙速度 考点二    人造卫星　宇宙速度 < 基础知识 > 二    同步卫星的五个“一定” 一、卫星的轨道参量随轨道半径变化的规律 　　由表可知:随卫星轨道半径的增加,卫星的向心加速度、线速度、 角速度都减小,运行周期将增大。 动力学特征 G   = ma n = m   = mω 2 r = m (   ) 2 r 向心加速度 a n a n = G   ,即 a n ∝   线速度 v v =   ,即 v ∝   角速度 ω ω =   ,即 ω ∝   周期 T T =   ,即 T ∝   < 重点难点 > 例1     (2013上海单科,22B,4分)若两颗人造地球卫星的周期之比为 T 1 ∶ T 2 =2∶1,则它们的轨道半径之比 R 1 ∶ R 2 = 　　　     ,向心加速度之比 a 1 ∶ a 2 = 　　　　     。 解题导引   解析 　由   = m ·   · R 得   =   =   ∶1 由   = ma 得   =   =   =1∶2   。   答案        ∶1　1∶2   二、卫星变轨问题 卫星绕天体稳定运行时,万有引力提供了卫星做匀速圆周运动的向心 力。由 G   = m   ,得 v =   ,由此可知轨道半径 r (卫星到天体中心的 距离)越大,卫星的速度 v 越小。当卫星由于某种原因速度 v 突然改变时, F 万 和 m   不再相等,因此就不能再根据 v =   来确定 r 的大小。当 F 万 > m   时,卫星做“近心”运动;当 F 万 < m   时,卫星做“离心”运动。 例2     (2017河南三市二模,17)北京时间2016年10月17日7时30分,神舟十 一号飞船搭载两名航天员在酒泉卫星发射中心发射升空。10月19日凌 晨,神舟十一号飞船与天宫二号自动交会对接成功,航天员景海鹏和陈 冬入驻天宫二号空间实验室,开始为期30天的太空驻留生活。已知地球 表面的重力加速度 g ,地球半径 R ,神舟十一号飞船对接后随天宫二号做 匀速圆周运动的周期 T 及引力常量 G ,下列说法中正确的是   (　　) A.要完成对接,应先让神舟十一号飞船和天宫二号处于同一轨道上,然 后点火加速 B.若对接前飞船在较低轨道上做匀速圆周运动,对接后飞船速度和运行 周期都增大 C.由题给条件可求出神舟十一号飞船的质量 D.由题给条件可求出神舟十一号飞船对接后距离地面的高度 h 解题导引   解析 　若神舟十一号飞船与天宫二号在同一轨道上,神舟十一号飞船 受到的万有引力等于向心力,若让神舟十一号飞船加速,其所需要的向 心力变大,而此时万有引力不变,所以神舟十一号飞船做离心运动,不能 实现对接,故A错误;根据万有引力提供向心力: G   = m   ,得 v =   , 对接后轨道半径变大,则线速度变小,故B错误;由题给条件不能求出神 舟十一号飞船的质量,故C错误;根据万有引力提供向心力有: G   = m   ,其中 r = R + h ,又 GM = gR 2 ,得 h =   - R ,故D正确。   答案     D 　 天体运动中的双星问题思考方法 1. 宇宙中存在独立的双星系统、三星系统、四星系统等,它们的共同特 点是系统中各星的角速度相等,各自所需的向心力由彼此间的万有引力 提供。 2. 宇宙中四分之三以上的星体以双星的形式存在。被相互引力系在一 起,互相绕转的两颗星就叫物理双星。双星是绕公共圆心转动的一对恒 星。如图所示双星系统具有以下几个特点: 方法 技巧 方法 1   (1)各自需要的向心力由彼此间的万有引力提供,即   = m 1   r 1 ,   = m 2   r 2 (2)两颗星的周期及角速度都相同,即 T 1 = T 2 , ω 1 = ω 2 (3)两颗星的运动轨道半径与它们之间的距离关系为 r 1 + r 2 = L (4)两颗星到轨道圆心的距离 r 1 、 r 2 与星体质量成反比   =   (5)双星的运动周期 T =2π   (6)双星的总质量 m 1 + m 2 =   例1     (2013山东理综,20,5分)双星系统由两颗恒星组成,两恒星在相互 引力的作用下,分别围绕其连线上的某一点做周期相同的匀速圆周运 动。研究发现,双星系统演化过程中,两星的总质量、距离和周期均可 能发生变化。若某双星系统中两星做圆周运动的周期为 T ,经过一段时 间演化后,两星总质量变为原来的 k 倍,两星之间的距离变为原来的 n 倍, 则此时圆周运动的周期为   (　　) A.   T 　    B.   T 　    C.   T 　    D.   T   解析 　设双星质量各为 m 1 、 m 2 ,相距 L ,做圆周运动的半径分别为 r 1 、 r 2 ,则 G   = m 1   G   = m 2   r 1 + r 2 = L 可得   =   T =   所以 T '=   T 故B正确,A、C、D错误。   答案     B 　 估算题的解答方法 1. 物理估算,一般是依据一定的物理概念和规律,运用近似计算方法,对 物理量的数值或取值范围进行大致的推算。 2. 物理估算是一种重要方法,有的物理问题,在符合精确度的前提下,可 以用近似的方法简捷处理;有的物理问题,由于本身条件的特殊性,不需 要也不可能进行精确计算,在这种情况下,估算就成为一种既符合科学 规律又有实用价值的特殊方法。 3. 有一些天体运动方面的估算题,常需要利用一些隐含条件或生活中的 物理常识,应有意识地加以利用。如:在地球表面的物体受到的万有引 力近似等于重力;地球表面附近重力加速度 g =9.8 m/s 2 ,地球自转周期 T = 24 h,公转周期 T '=365天,月球绕地球公转周期约为27天等。 方法 2 例2 　已知太阳到地球与地球到月球的距离的比值约为390,月球绕地球 旋转的周期约为27天。利用上述数据以及日常的天文知识,可估算出太 阳对月球与地球对月球的万有引力的比值约为   (　　) A.0.2　　　    B.2　　　    C.20　　　    D.200   解析 　设太阳到地球的距离为 R ,地球到月球的距离为 r ,太阳、地球和 月球的质量分别为 m S 、 m E 和 m 。由万有引力定律可知太阳对月球的万 有引力 F 1 =   (太阳到月球距离近似等于太阳到地球距离)。地球对 月球的万有引力 F 2 =   。两式联立得   =   。若地球和月球的公 转均看做匀速圆周运动,由万有引力提供向心力可知,对地球:   =   , T E 为地球公转周期365天,对月球:   =   , T m 为月球公转 周期27天。联立得   =   ,故有   =   =   ≈ 2。选B。   答案     B 　 第一宇宙速度的求解方法 第一宇宙速度: v 1 =7.9 km/s,是物体在地球表面附近绕地球做匀速圆周运 动的最大环绕速度,也是在地面上发射卫星的最小发射速度。其计算方 法有以下两种: 方法一　设想在地球表面附近有一颗人造地球卫星,地球对卫星的万有 引力提供卫星做圆周运动的向心力,由 G   = m   ,得到 v =   。因为 R ≫ h ,所以 v ≈   ,若已知地球的质量和半径,则可计算 第一宇宙速度的值。 方法二　设想在地球表面附近有一颗人造地球卫星,它受到的重力近似 地等于地球对物体的万有引力,而万有引力提供了卫星做圆周运动的向 方法 3 心力,由 mg = m   得到 v =   。因为 R ≫ h ,所以 v ≈   ,若已知地 球表面附近的重力加速度和地球半径,则可计算出第一宇宙速度的值。 例3     (2014福建理综,14,6分)若有一颗“宜居”行星,其质量为地球的 p 倍,半径为地球的 q 倍,则该行星卫星的环绕速度是地球卫星环绕速度的   (　　) A.   倍　    B.   倍 C.   倍　    D.   倍   解析 　对于中心天体的卫星, G   = m   , v =   ,设该行星卫星的环 绕速度为 v ',地球卫星的环绕速度为 v ,则   =   =   ,C正确。   答案     C 　 随地球转和绕地球转问题的分析 同步卫星既是卫星又可看做地球赤道表面的连续物,因此赤道上随地球 自转的物体利用同步卫星这一“中介”可与地球卫星进行比较。 1.轨道半径: 近地卫星与赤道上物体的轨道半径相同,同步卫星的轨道半 径较大, r 同 > r 近 = r 物 。 2.运行周期: 同步卫星与赤道上物体的运行周期相同。由 T =2π   可 知,近地卫星的周期要小于同步卫星的周期, T 近 < T 同 = T 物 。 3.向心加速度: 由 G   = ma 知,同步卫星的向心加速度小于近地卫星的 向心加速度。 由 a = rω 2 = r   知,同步卫星的向心加速度大于赤道上物体的向心加速 方法 4 度, a 近 > a 同 > a 物 。 4.动力学规律: 近地卫星和同步卫星都只受到万有引力作用,由万有引力 充当向心力。满足万有引力充当向心力所决定的天体运行规律。赤道 上的物体由万有引力和地面支持力的合力充当向心力(或说成万有引 力的分力充当向心力),它的运动规律不同于卫星的运动规律。 例4 　同步卫星离地心距离 r ,运行速度为 v 1 ,加速度为 a 1 ,地球赤道上的物 体随地球自转的加速度为 a 2 ,第一宇宙速度为 v 2 ,地球半径为 R ,则以下正 确的是   (　　) A.   =   　    B.   =   C.   =   　    D.   =     解析　 设地球质量为 M ,同步卫星的质量为 m 1 ,地球赤道上的物体质量 为 m 2 ,在地球表面附近飞行的物体的质量为 m 2 ',根据向心加速度和角速 度的关系有 a 1 =   r , a 2 =   R , ω 1 = ω 2 ,故   =   ,可知选项A正确。 由万有引力定律有 G   = m 1   , G   = m 2 '   ,由以上两式解得   =   , 可知选项D正确。   答案     AD