2020届二轮复习第3讲　力与曲线运动课件（35张）（天津专用） 35页

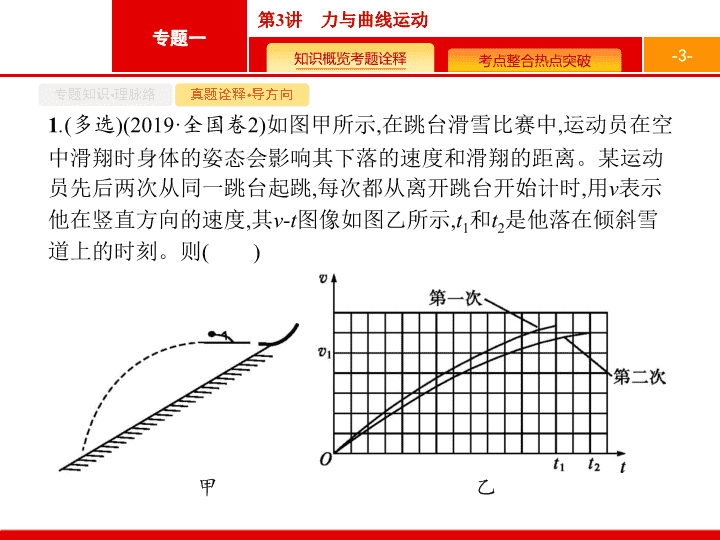
第 3 讲 　 力与曲线运动 - 2 - 专题知识 • 理脉络 真题诠释 • 导方向 - 3 - 专题知识 • 理脉络 真题诠释 • 导方向 1 . ( 多选 )(2019· 全国卷 2) 如图甲所示 , 在跳台滑雪比赛中 , 运动员在空中滑翔时身体的姿态会影响其下落的速度和滑翔的距离。某运动员先后两次从同一跳台起跳 , 每次都从离开跳台开始计时 , 用 v 表示他在竖直方向的速度 , 其 v - t 图像如图乙所示 , t 1 和 t 2 是他落在倾斜雪道上的时刻。则 ( 　　 ) - 4 - 专题知识 • 理脉络 真题诠释 • 导方向 A. 第二次滑翔过程中在竖直方向上的位移比第一次的小 B. 第二次滑翔过程中在水平方向上的位移比第一次的大 C. 第二次滑翔过程中在竖直方向上的平均加速度比第一次的大 D. 竖直方向速度大小为 v 1 时 , 第二次滑翔在竖直方向上所受阻力比第一次的大 答案 : BD 　 解析 : 从 v - t 图像中 , 图线与坐标轴所围面积可知第二次面积大于第一次面积 , 故第二次在竖直方向上的位移比第一次的大 ,A 错误 ; 因为沿斜面位移方向不变 , 而第二次竖直位移大 , 因此第二次水平位移也大 ,B 正确 ; 从题图中可以得出 , 第一次斜率大于第二次的斜率 , 斜率越大 , 说明加速度越大 , 因此 C 错误 ; 在竖直方向上根据牛顿第二定律 mg-F f =ma , 加速度大的阻力小 ,D 正确。 - 5 - 专题知识 • 理脉络 真题诠释 • 导方向 命题考点 平抛运动 , 运动的合成和分解。 能力要求 本题主要考查平抛运动 , 读懂 v - t 图像 , 知道 v - t 图像中加速度与位移的表示方法是正确解题的关键。 - 6 - 专题知识 • 理脉络 真题诠释 • 导方向 2 . (2018· 全国卷 3) 在一斜面顶端 , 将甲、乙两个小球分别以 v 和 的 速度沿同一方向水平抛出 , 两球都落在该斜面上。甲球落至斜面时的速率是乙球落至斜面时速率的 ( 　　 ) A.2 倍 B.4 倍 C.6 倍 D.8 倍 A 解析 : 设斜面倾角为 θ , 小球从斜面上水平抛出又落到斜面上 , 对于 任 速度之比就是初速度之比 , 选项 A 正确 。 - 7 - 专题知识 • 理脉络 真题诠释 • 导方向 命题考点 平抛运动。 能力要求 掌握运动的合成与分解 , 结合数学知识 分析速度 关系。 - 8 - 专题知识 • 理脉络 真题诠释 • 导方向 3 . (2018· 天津卷 ) 滑雪运动深受人民群众喜爱。某滑雪运动员 ( 可视为质点 ) 由坡道进入竖直面内的圆弧形滑道 AB , 从滑道的 A 点滑行到最低点 B 的过程中 , 由于摩擦力的存在 , 运动员的速率不变 , 则运动员沿 AB 下滑过程中 ( 　　 ) A. 所受合外力始终为零 B. 所受摩擦力大小不变 C. 合外力做功一定为零 D. 机械能始终保持不变 C - 9 - 专题知识 • 理脉络 真题诠释 • 导方向 解析 : 运动员从滑道 A 点滑行到 B 点过程中做匀速圆周运动 , 合外力提供向心力 , 合外力不等于零且方向始终指向圆心 , 故合外力不做功 , 选项 A 错误、 C 正确 ; 由于运动员从滑道 A 点到 B 点过程中做匀速圆周运动 , 故切向合力为零 , 摩擦力等于重力沿切向的分力 , 大小不断变化 , 选项 B 错误 ; 运动员运动过程要克服摩擦力做功 , 故机械能减小 , 选项 D 错误。 命题考点 圆周运动 , 功能关系。 能力要求 正确理解圆周运动特点 , 抓住运动员做的是匀速圆周运动 , 速率不变 , 而速度、加速度、合外力是变化的。 - 10 - 专题知识 • 理脉络 真题诠释 • 导方向 4 . (2018· 全国卷 3) 如图所示 , 在竖直平面内 , 一半径为 R 的光滑圆弧轨道 ABC 和水平轨道 PA 在 A 点相切。 BC 为圆弧轨道的直径 , O 为圆心 , OA 和 OB 之间的夹角为 α ,sin α = 。 一质量为 m 的小球沿水平轨道向右运动 , 经 A 点沿圆弧轨道通过 C 点 , 落至水平轨道 ; 在整个过程中 , 除受到重力及轨道作用力外 , 小球还一直受到一水平恒力的作用。已知小球在 C 点所受合力的方向指向圆心 , 且此时小球对轨道的压力恰好为零。重力加速度大小为 g 。求 : (1) 水平恒力的大小和小球到达 C 点时速度 的 大小 ; (2) 小球到达 A 点时动量的大小 ; (3) 小球从 C 点落至水平轨道所用的时间。 - 11 - 专题知识 • 理脉络 真题诠释 • 导方向 解析 : (1) 设水平恒力的大小为 F 0 , 小球到达 C 点时所受合力的大小为 F , 由力的合成法则有 - 12 - 专题知识 • 理脉络 真题诠释 • 导方向 (2) 设小球到达 A 点的速度大小为 v 1 , 作 CD ⊥ PA , 交 PA 于 D 点 , 由几何关系得 l DA =R sin α ⑥ l CD =R (1 + cos α ) ⑦ 由动能定理有 由 ④⑤⑥⑦⑧ 式和题给数据得 , 小球在 A 点的动量大小 为 - 13 - 专题知识 • 理脉络 真题诠释 • 导方向 (3) 小球离开 C 点后在竖直方向上做初速度不为零的匀加速运动 , 加速度大小为 g 。设小球在竖直方向的初速度为 v ⊥ , 从 C 点落至水平轨道上所用时间为 t 。由运动学公式有 命题考点 圆周运动、抛体运动、动能定理、动量。 能力要求 熟练掌握力与运动的合成与分解 , 注意几何关系的 分析 , 结合 动能定理 分析 解答。 - 14 - 突破点一 突破点二 突破点三 曲线运动的理解 考查方向 常以选择题的形式考查对曲线运动的理解 , 关联速度问题。 突破方略 1 . 物体做曲线运动的条件及特点 (1) 条件 : F 合 与 v 的方向不在同一直线上 , 或加速度方向与速度方向不共线。 (2) 特点 : ① F 合 恒定 : 做匀变速曲线运动。 ② F 合 不恒定 : 做非匀变速曲线运动。 ③ 做曲线运动的物体受的合力总是指向曲线的凹侧。 - 15 - 突破点一 突破点二 突破点三 2 . 绳 ( 杆 ) 关联物体的速度 (1) 若由绳 ( 杆 ) 连接的两运动物体的运动方向沿绳 ( 杆 ) 方向 , 则两物体速度大小相等。 (2) 若物体运动方向不沿绳 ( 杆 ) 方向 , 将其速度分解到沿绳 ( 杆 ) 方向和垂直绳 ( 杆 ) 方向 , 再参考上一条。 - 16 - 突破点一 突破点二 突破点三 模型构建 【例 1 】 (2019· 天津七校联考 ) 如图所示 , 质量为 m 的物体 P 置于倾角为 θ 1 的固定光滑斜面上 , 斜面足够长 , 轻细绳跨过光滑定滑轮分别连接着 P 与动力小车 ,P 与滑轮间的细绳平行于斜面 , 小车带动物体 P 以速率 v 沿斜面匀速运动 , 下列判断正确的是 ( 　　 ) A. 小车的速率为 v B. 小车的速率为 v cos θ 1 C. 小车速率始终大于物体 P 的速率 D. 小车做匀变速运动 C - 17 - 突破点一 突破点二 突破点三 解析 : 将小车的速度沿绳子方向和垂直于绳子方向分解 , 沿绳子方向的速度大小等于 P 的速度大小 , 则有 v=v 车 cos θ 2 , 可知小车的速率与 θ 2 有关 , 不是匀变速运动 , 且始终大于物体 P 的速率 , 故 C 正确 ,A 、 B 、 D 错误。 以题说法 解决运动合成和分解的一般思路 (1) 明确合运动或分运动的运动性质。 (2) 明确是在哪两个方向上的合成或分解。 (3) 找出各个方向上已知的物理量 ( 速度、位移、加速度 ) 。 (4) 运用力与速度的关系或矢量的运算法则进行 分析求解 。 - 18 - 突破点一 突破点二 突破点三 迁移训练 1 . ( 多选 )(2019· 山东淄博摸底 ) 如图所示 , 在一端封闭的光滑细玻璃管中注满清水 , 水中放一红蜡块 R(R 视为质点 ) 。将玻璃管的开口端用胶塞塞紧后竖直倒置且与 y 轴重合 , 在红蜡块 R 从坐标原点匀速上浮的同时 , 玻璃管沿 x 轴正向做初速度为零的匀加速直线运动 , 合速度的方向与 y 轴夹角为 α 。则红蜡块 R 的 ( 　　 ) A. 分位移 y 与分位移 x 成正比 B. 合速度 v 的大小与时间 t 成正比 C. 分位移 y 的二次方与分位移 x 成正比 D.tan α 与时间 t 成正比 CD - 19 - 突破点一 突破点二 突破点三 解析 : 红蜡块 R 的运动可分解为沿 x 轴正方向做初速度为零的匀 - 20 - 突破点三 突破点一 突破点二 平抛运动规律的理解与应用 考查方向 常以选择题形式考查 , 或与功能关系综合考查。 突破方略 1 . 求解平抛运动的基本思路和方法 —— 运动的分解 将平抛运动分解为水平方向的匀速直线运动和竖直方向的自由落体运动 ——“ 化曲为直 ”, 是处理平抛运动的基本思路和方法 。 - 21 - 突破点三 突破点一 突破点二 2 . 两个基本 关系 分析题目 条件是位移 ( 方向 ) 关系 , 还是速度 ( 方向 ) 关系 , 选择合适的关系式解题。 - 22 - 突破点三 突破点一 突破点二 模型构建 【例 2 】 ( 多选 )(2019· 山东六校联考 ) 如图所示 , D 点为固定斜面 AC 的中点。在 A 点和 D 点分别以初速度 v 01 和 v 02 水平抛出一个小球 , 结果两球均落在斜面的底端 C 。空气阻力不计。设两球在空中运动的时间分别为 t 1 和 t 2 , 落到 C 点前瞬间的速度大小分别为 v 1 和 v 2 , 落到 C 点前瞬间的速度方向与水平方向的夹角分别为 θ 1 和 θ 2 , 则下列关系式正确的是 ( 　　 ) BC - 23 - 突破点三 突破点一 突破点二 解析 : 由题意知两小球做平抛运动的竖直位移之比为 2 ∶ 1, 由 平 分析 , 可知 v 1 、 v 2 与水平方向的夹角 θ 1 、 θ 2 的正切值也相等 ,D 项错误。 - 24 - 突破点三 突破点一 突破点二 分析推理 (1) 平抛的时间由哪个物理量决定 ? (2) 速度偏转角的正切如何求解 ? (1) 提示 : 高度 。 - 25 - 突破点三 突破点一 突破点二 以题说法 抓住 “ 六点 ” 破解平抛运动问题 (1) 建立坐标 , 分解运动 将平抛运动分解为竖直方向的自由落体运动和水平方向上的匀速直线运动 , 而类平抛运动分解的方向不一定在竖直方向和水平方向上。 (2) 各自独立 , 分别分析 (3) 平抛运动是匀变速曲线运动 , 在任意相等的时间内速度的变化量 Δ v 相等 ,Δ v=g Δ t , 方向恒为竖直向下。 - 26 - 突破点三 突破点一 突破点二 (4) 两个分运动与合运动具有等时性 , 且 t = , 由下落高度决定 , 与初速度 v 0 无关。 (5) 任意时刻的速度与水平方向的夹角 θ 的正切值总等于该时刻的位移与水平方向的夹角 φ 的正切值的 2 倍 , 即 tan θ = 2tan φ 。 (6) 建好 “ 两个模型 ” ① 常规的平抛运动及类平抛模型。 ② 与斜面相结合的平抛运动模型。 a. 从斜面上水平抛出又落回到斜面上 : 位移方向恒定 , 落点速度方向与斜面间的夹角恒定 , 此时往往分解位移 , 构建位移三角形。 b. 从斜面外水平抛出垂直落在斜面上 : 速度方向确定 , 此时往往分解速度 , 构建速度三角形。 - 27 - 突破点三 突破点一 突破点二 迁移训练 2 . (2019· 河南郑州质量预测 ) 如图所示 , 圆环竖直放置 , 从圆心 O 点正上方的 P 点 , 以速度 v 0 水平抛出的小球恰能从圆环上的 Q 点沿切线方向飞过 , 若 OQ 与 OP 间夹角为 θ , 不计空气阻力 , 重力加速度为 g 。则 ( 　　 ) D - 28 - 突破点三 突破点一 突破点二 解析 : 根据几何关系知 , 小球在 Q 点的速度方向与水平方向的 夹角 - 29 - 突破点三 突破点一 突破点二 圆周运动问题 考查方向 常以选择题形式考查圆周运动相关问题 , 也常与功能关系综合考查。 突破方略 1 . 解决圆周运动动力学问题的关键 (1) 圆周运动动力学问题的实质是牛顿第二定律的应用 , 且已知合外力方向 ( 匀速圆周运动合外力方向指向圆心 ), 要做好受力 分析 , 由牛顿第二定律列方程求合外力。 (2) 做匀速圆周运动的物体 , 所受合外力提供向心力。 (3) 做非匀速圆周运动的物体 , 所受合外力沿半径方向的分力提供向心力 , 沿切线方向的分力改变速度的大小。 - 30 - 突破点三 突破点一 突破点二 2 . 竖直平面内圆周运动的两种临界 问题 其实圆周轨道上比圆心高的点都有自己的临界速度 , 小球的速度小于临界速度时就会以斜上抛的方式脱离圆周轨道 ; 在比圆心低的点 , 小球的速度可以减小到 0 而不脱离轨道 , 如果轨道光滑的话会沿圆周轨道滑下去。 (2) 杆球模型 : 小球能到达最高点的条件是 v ≥ 0 。 - 31 - 突破点三 突破点一 突破点二 模型构建 【例 3 】 两个质量分别为 2 m 和 m 的小木块 a 和 b( 可视为质点 ) 放在水平圆盘上 ,a 与转轴 OO' 的距离为 l ,b 与转轴的距离为 2 l ,a 、 b 之间用长为 l 的强度足够大的轻绳相连 , 木块与圆盘的最大静摩擦力为木块所受重力的 k 倍 , 重力加速度大小为 g 。若圆盘从静止开始绕转轴缓慢地加速转动 , 开始时轻绳刚好伸直但无拉力 , 用 ω 表示圆盘转动的角速度 , 下列说法正确的是 ( 　　 ) A.a 比 b 先达到最大静摩擦力 B.a 、 b 所受的摩擦力始终相等 D - 32 - 突破点三 突破点一 突破点二 解析 : 木块随圆盘一起转动 , 当绳子上无拉力时 , 静摩擦力提供 向 着 ω 增大 ,b 先达到临界角速度 ,b 先达到最大静摩擦力 , 故 A 错误。在 b 的摩擦力没有达到最大前 , 由 F f =m ω 2 r ,a 、 b 质量分别是 2 m 和 m , 而圆周运动的半径 r 分别为 l 和 2 l , 所以开始时 a 和 b 受到的摩擦力是 相 kmg+F=m ω 2 · 2 l , 对于 a 木块有 F f ’ - F= 2 m ω 2 l , 联立得 F f ’= 4 m ω 2 l-kmg > kmg , 可知二者受到的摩擦力不一定相等 , 故 B 错误。 b 刚要滑动时 , - 33 - 突破点三 突破点一 突破点二 分析推理 (1)a 、 b 木块与圆盘发生相对滑动的临界条件是什么 ? (2) 绳子上何时出现拉力 ? (1) 提示 : 静摩擦力达到最大值。 (2) 提示 : b 木块和圆盘间静摩擦力达最大值时。 - 34 - 突破点三 突破点一 突破点二 迁移训练 3 . ( 多选 )(2019· 湖北黄冈期末调研 ) 如图所示 , 置于竖直面内的光滑金属圆环半径为 r , 质量为 m 的带孔小球穿于环上 , 同时有一长为 r 的细绳一端系于圆环最高点 , 另一端系在小球上 , 当圆环以角速度 ω ( ω ≠0) 绕竖直直径转动时 ( 　　 ) A. 细绳对小球的拉力可能为零 B. 细绳和金属圆环对小球的作用力大小可能相等 C. 细绳对小球拉力与小球的重力大小不可能相等 CD - 35 - 突破点三 突破点一 突破点二 解析 : 因为圆环光滑 , 故小球可能受三个力的作用 , 分别是重力、环对球的弹力、细绳的拉力 , 根据几何关系可知 , 此时细绳与竖直方向的夹角为 60 ° , 当圆环旋转时 , 小球绕竖直轴做圆周运动 , 则有 F T cos 60 ° +F N cos 60 ° =mg , F T sin 60 ° -F N sin 60 ° =m ω 2 r sin 60 ° , 故 C 、 D 正确 ,A 、 B 错误 。