【物理】2020届高考物理二轮复习能量和动量专题强化（3）重力势能和弹性势能A 11页

重力势能和弹性势能 A 1、取水平地面为重力势能零点,一小球从距地某高度处自由下落,经过时间 t 到达 A 处,在 A 处的重力势能与动能的比值 EpA:EkA=4,再经过时间 t 到达 B 处,则在 B 处的动能与重力势能 的比值 EkB:EpB 为( ) A.5 B.4 C.3 D.2 2、如图所示,质量为 m 的跳高运动员先后用背越式和跨越式两种跳高方式跳过某一高度,该 高度比他起跳时的重心高出 h,则他从起跳至跃过横杆的过程中克服重力所做的功( ) A.都必须大于 B.都不一定大于 C.用背越式不一定大于 ,用跨越式必须大于 D.用背越式必须大于 ,用跨越式不一定大于 3、如图所示,质量相等的 两物体之间连接一轻弹簧,竖直放在水平地面上,今用力 F 缓慢 向上拉 A,直到 B 刚要离开地面,设开始时弹簧的弹性势能为 刚要离开地面时弹簧的弹 性势能为 ,则( ) A. B. C. 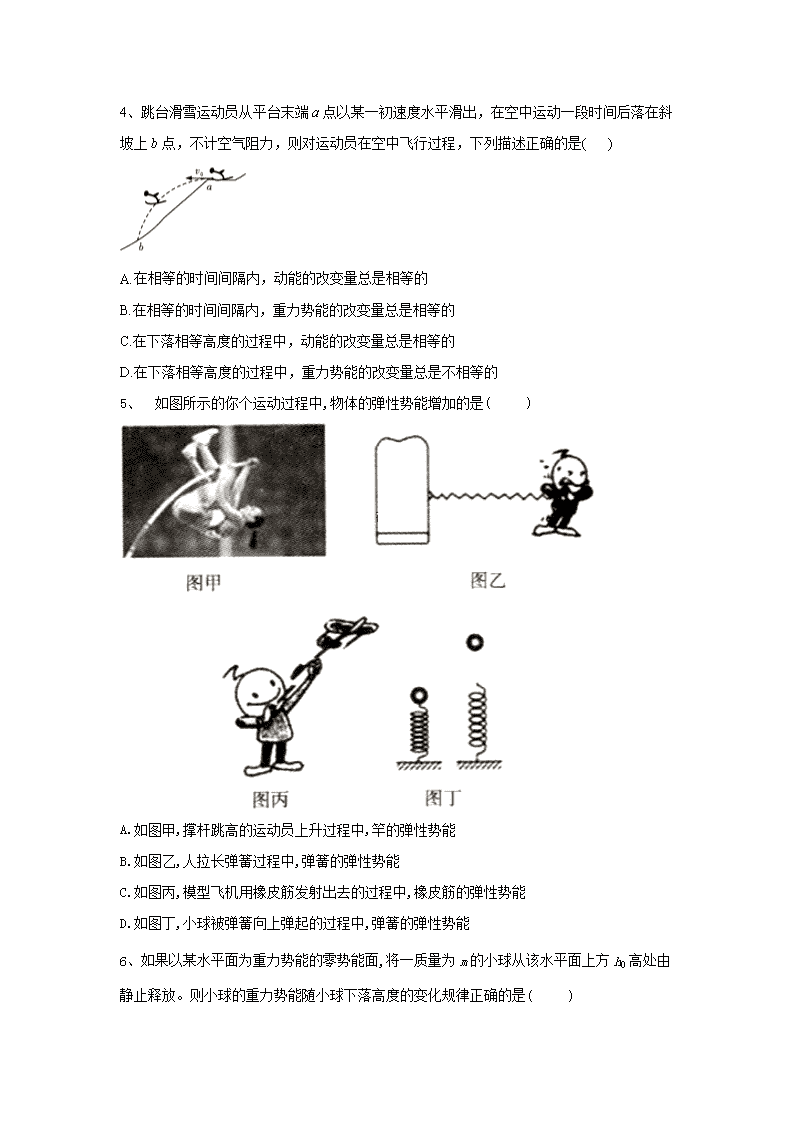D.无法确定 mgh mgh mgh mgh mgh mgh A B、 p1,E B p2E p1 p2E E> p1 p2E E= p1 p2E E< 4、跳台滑雪运动员从平台末端 a 点以某一初速度水平滑出，在空中运动一段时间后落在斜 坡上 b 点，不计空气阻力，则对运动员在空中飞行过程，下列描述正确的是( ) A.在相等的时间间隔内，动能的改变量总是相等的 B.在相等的时间间隔内，重力势能的改变量总是相等的 C.在下落相等高度的过程中，动能的改变量总是相等的 D.在下落相等高度的过程中，重力势能的改变量总是不相等的 5、 如图所示的你个运动过程中,物体的弹性势能增加的是( ) A.如图甲,撑杆跳高的运动员上升过程中,竿的弹性势能 B.如图乙,人拉长弹簧过程中,弹簧的弹性势能 C.如图丙,模型飞机用橡皮筋发射出去的过程中,橡皮筋的弹性势能 D.如图丁,小球被弹簧向上弹起的过程中,弹簧的弹性势能 6、如果以某水平面为重力势能的零势能面,将一质量为 m 的小球从该水平面上方 h0 高处由 静止释放。则小球的重力势能随小球下落高度的变化规律正确的是( ) A. B. C. D. 7、在一次演示实验中,一压紧的弹簧沿一粗糙水平面射出一小球,测得弹簧压缩的距离 d 和 小球在粗糙水平面上滚动的距离 s 如下表所示。由此表可以归纳出小球滚动的距离 s 跟弹簧 压缩的距离 d 之间的关系,并猜测弹簧的弹性势能 Ep 跟弹簧压缩的距离 d 之间的关系分别 是(选项中 k1、k2 是常量)( ) 实验次数 1 2 3 4 d/cm 0.50 1.00 2.00 4.00 s/cm 4.98 20.02 80.10 319.5 A.s=k1d,Ep=k2d B.s=k1d,Ep=k2d2 C.s=k1d2,Ep=k2d D.s=k1d2,Ep=k2d2 8、一根质量为 m、长为 L 的均匀链条一半放在光滑的水平桌面上,另一半悬在桌边,桌面足够 高,如图所示。若将一个质量为 m 的小球分别拴在链条左端和右端,如图 b、c 所示。约束链 条的挡板光滑,三种情况均由静止释放链条,当整根链条刚离开桌面时,关于它们的重力势能 的变化,下列判断中正确的是( ) A. B. C. D. 9、抽水蓄能电站的工作原理:在用电低谷时(如深夜),电站利用电网多余电能把水抽到高处蓄 水池中,到用电高峰时,再利用蓄水池中的水发电。如图所示,蓄水池(上游水库)可视为长方体, 有效总库容量(可用于发电)为 V,蓄水后水位高出下游水面 H,发电过程中上游水库水位最大 落差为 d。统计资料表明,该电站年抽水用电为 ,年发电量为 。则 下列计算结果正确的是(水的密度为 ρ,重力加速度为 g,涉及重力势能的计算均以下游水面为 参考平面)( ) A.能用于发电的水的最大重力势能 B.能用于发电的水的最大重力势能 C.电站的总效率达 75% D.该电站平均每天所发电能可供给一个大城市居民用电(电功率以 计)约 10h 10、如图所示,在粗糙斜面顶端固定一弹簧,其下端挂一物体,物体在 A 点处于平衡状态。现 用平行于斜面向下的力拉物体,第一次直接拉到 B 点,第二次将物体先拉到 C 点,再回到 B 点, 则这两次( ) pa pb pcE E E∆ = ∆ = ∆ pa pb pcE E E∆ = ∆ < ∆ pa pb pcE E E∆ < ∆ = ∆ pa pb pcE E E∆ < ∆ < ∆ 82.4 10 kW h× ⋅ 81.8 10 kW h× ⋅ pE VgHρ= p ( )2 dE Vg Hρ= − 510 kW A.重力势能改变量相等 B.弹簧的弹性势能改变量相等 C.摩擦力对物体做的功相等 D.弹簧弹力对物体做功相等 11、如图所示,某工地上的塔吊将质量为 m 的重物从静止开始竖直吊起,若绳子对重物的拉力 恒为 F,重物所受空气阻力恒为 f,重力加速度为 g,在重物上升 h 的过程中,下列说法正确的 是（ ） A.重物可能做加速度逐渐减小的加速运动 B.重物上升 h 时的速度大小为 C.重物重力做的功为-mgh D.重物的重力势能增加 Fh 12、根轻弹簧下端固定在水平地面上,一个质量为 m 的小球(可视为质点),从距弹簧上端 h 处 的 O 点自由下落并压缩弹簧,如图所示.若以小球下落点 O 点为 x 轴正方向起点和计时起点, 设小球从开始下落到接触弹簧所用时间为 t1,到压缩弹簧至最大位置下落高度为 H,所用时 间为 t3,不计任何阻力,弹簧均处于弹性限度内;小球下落过程中加速度 a、速度 v、弹簧的 弹力 F、弹性势能 Ep 变化的图像正确的是( ) 2 F f g hm − −   A. B. C. D. 13、如图所示,圆柱形水箱高为 5m,容积为 ,水箱底部接通水管 A,顶部接通水管 B,开始时 箱中无水,若仅使用 A 管或仅使用 B 管慢慢地将水注入,直到箱中水满为止,g 取 。试计 算两种情况下外界各需做多少功?(设需注入的水开始时均与箱底等高) 14、光滑水平桌面上，质量为 m=1kg 的木块(视为质点)左端与轻弹簧相连，弹簧的另一端固 定。木块的右端与一轻细线连接，细线绕过光滑的质量不计的轻滑轮，木块开始静止在 O 点， 弹簧处于原长。在细线的另一端施加一竖直向下的大小为 F=10N 的恒力，如图甲所示，木块 从 O 点由静止开始向右运动。当木块运动至 P 点时，速度大小为 v=1m/s，O、P 两点间的距 离为 l =0.1m。（弹簧均处于弹性限度内，不计空气阻力和线的形变，重力加速度 g 取 。) 350m 210m/s 210 /m s 1.求木块运动至 P 点时弹簧的弹性势能。 2.如果在细线的另一端悬挂一个质量为 M =3kg 的重物，如图乙所示，木块从初始位置 O 由 静止开始向右运动，求当木块通过 P 点时的速度大小。 3.已知在弹性限度内，劲度系数为 k，形变量为 x 时，弹簧的弹性势能为 。在第 2 问给出的条件下，求出重物 M 由静止下落到最低点过程中的最大速度是多少？ 答案以及解析 1 答案及解析： 答案：B 解析：设开始时小球离地面的高度为 H,根据自由落体运动的规律可知,两段时间内的高度之 比为 1:3,设为 h 和 3h,由能量关系可知: ,解得 H=5h;到达 B 点时: ,故选 B. 2 答案及解析： 答案：C 解析：从图中可看出,背越式越过横杆时运动员的重心可能在腰部下方,即重心可能在横杆的 下方;而跨越式跨过横杆时,运动员的重心一定在横杆之上。故 C 正确。 3 答案及解析： 答案：B 21 2pE kx= ( ) 4,pA kA E mg H h E mgh ⋅ −= = 4,( 4 ) kB pB E mg h E m H h ⋅ 4= =− 解析：对于同一弹簧,其弹性势能的大小取决于它的形变量。开始时,弹簧处于压缩状态,与原 长相比,它的压缩量为 。当 B 刚要离开地面时,弹簧处于拉伸状态,与原长相比,它的 伸长量为 。因为 ,所以 ,故 。 4 答案及解析： 答案：C 解析：由题意可知，动能的改变量与重力做功有关，由于在相等的时问间隔内竖直方向运动 的位移不相等，所以重力在相等的时间间隔内做功也不相等.则重力势能的改变量不相等， 动能的改变量也不相等，故 AB 错误;在下落相等高度的过程中，重力做功相等，重力势能 的改变量总是相等的，动能的改变量总是相等的，故 C 正确.D 错误。 5 答案及解析： 答案：B 解析：选项 A、C、D 中形变量都在减小,所以弹性势能减小,选项 B 中弹簧的形变量增大,所 以弹性势能增加,所以 B 正确。 6 答案及解析： 答案：B 解析：设小球开始下落时的重力势能为 ,小球下落高度 h 的过程中重力势能减少量 ,故小球下落高度 h 时的重力势能 ,即 Ep—h 图象 为倾斜直线,B 正确。 7 答案及解析： 答案：D 解析：分析实验数据,可看出在误差允许的范围内 ,即 。由生活常识课猜测, 弹性势能越小,小球滚动的距离越远, ,则 , 。 8 答案及解析： 1 Am gl k ∆ = 2 Bm gl k ∆ = A Bm m= 1 2l l∆ = ∆ p1 p2E E= 0pE pE mgh∆ = 0 0p p p pE E E E mgh= − ∆ = − 2 20s d = 2 1s k d= pE s∝ 2 pE d∝ 2 2pE k d= 答案：B 解析：将图 a 中链条分为等长两部分,减小的重力势能共为 。将图 b 中系统分为球与两段等长链条三部分,由于球的 重心高度不变,故系统减少的重力势能与图 a 中相同。在图 c 中仍分为球与两段等长链条三 部分,链条的重力势能变化与前两图中相同,系统减少的重力势能等于链条与小球减少的重力 势能之和,故系统减少的重力势能共为 ,故 B 正确。 9 答案及解析： 答案：BC 解析：以下游水面为参考平面,则用于发电的水的重心位置高出下游水面 ,故其最大 重力势能 ,A 错误,B 正确;电站的总效率 ,故 C 正确;设该电站平均每天发电可供一个大城市 居民用电时间为 t,则: ,代入数据得 ,故 D 错误。 10 答案及解析： 答案：ABD 解析：重力(弹簧的弹力)做的功等于重力势能(弹性势能)的减少量,重力(弹簧的弹力)做功 与路径无关,所以两次重力势能(弹簧的弹性势能)改变量相等,ABD 正确;摩擦力做功与路径 有关,两次摩擦力做的功不等,C 错误。 11 答案及解析： 答案：BC 解析：根据题述，绳子对重物的拉力恒为 F,重物所受空气阻力恒为 f,根据牛顿第二定律， 重物上升的加速度恒定，重物做匀加速直线运动，A 错误；由牛顿第二定律，有 ， 由匀变速直线运动规律，有 ，联立解得重物上升 h 时的速度 pa 1 1 3 2 2 2 4 8 L LE mg mg mgL∆ = × + × = pc 3 7 8 2 8 LE mgL mg mg∆ = + × = 2 dH −   p 2 dE Vg Hρ  = −   8 8 1.8 10 J100% 100% 75%2.4 10 J W W η ×= × = × =× 有 总 365 WPt = 有 5ht ≈ F mg f ma− − = 2 2v ah= 大小为 ，B 正确；重物重力做的功 ，C 正确;根据功能关 系可知重物的重力势能增加 mgh，D 错误。 12 答案及解析： 答案：AD 解析：小球接触弹簧之前做自由落体运动,小球从开始压缩弹簧到把弹簧压缩到最短的过程 中,存在一个位置即小球的重力 G 与弹簧对小球的弹力 F 大小相等的位置,小球向下运动到 此位置的过程中 FG,小球做加速度增大的减速运动,选项 A 正确;小球接触弹簧之前速度均匀增加,接触 之后速度还是继续增加,然后再减小,选项 B 错误;弹簧的弹力 ,与位移呈线性关系, 选项 C 错误;弹簧的弹性势能 ,选项 D 正确。 13 答案及解析： 答案：以 H 表示水箱的高度,水若从 A 管注入,整箱水的重心被升高 ,外界做功 。若水从 B 管注入,整箱水应先升高 到箱顶处后再下落,故外界做的功 。 解析： 14 答案及解析： 答案：1.用力 F 拉木块至 P 点时，设此时弹簧的弹性势能为 E， 根据功能关系得 解得： 2.悬挂钩码 M 时，当木块运动到 P 点时，弹簧的弹性势能仍为 E，设木块的速度为 v′， 由机械能守恒定律得 解得 2 F fv g hm − = −   W mgh= − F k x= ∆ ( )2 p 1 2E k x= ∆ 2 H 3 6 1 51.0 10 50 10 J 1.25 10 J2 2 2 H HW mg Vgρ= ⋅ = ⋅ = × × × × = × 6 2 12 2.5 10 JW mgH W= = = × 21 2Fl Ep mv= 0.5pE J＝ 21 ( )2Mgl Ep m M v= + + 5 /2v m s′＝= 3.根据 ，解得 k=100N/m 当速度最大时，有 Mg=kx，解得弹簧的伸长量 x=0.3m 根据 ，解得 ，解得最大速度 解析： 21 2pE kl= 21 2pxE kx= 4.5pxE J= 21 ( )2px mMgx E m M v= + + 1.5 /mv m s=