【物理】2020届一轮复习人教版光的反射折射课时作业 18页

‎2020届一轮复习人教版 光的反射 折射 课时作业 ‎ 1、在空气中，一条光线以60°的入射角射到一平行玻璃板的上表面ab上，已知该玻璃的折射率为，下列说法正确的是（　　）‎ A．光线可能在ab面上发生全反射而不能进入玻璃板 B．光线肯定能从ab面进入玻璃板且折射角为30°‎ C．光线可能在cd面上发生全反射而不能射出玻璃板 D．光线肯定能从cd面射出玻璃板且折射角为30° 2、某同学将一枚大头针从一边长为6cm的正方形不透光的轻质薄板正中心垂直于板插入，制作成了一个测定液体折射率的简单装置．他将该装置放在某种液体液面上，调整大头针插入深度，当插入液体中深度为4cm时，恰好无论从液面上方任何方向都看不到液体中的大头针，则该液体的折射率为（　　）‎ A． B． C． D．‎ ‎　 3、如图所示，一束复色光沿PO射向截面为半圆形玻璃砖的圆心O处后，分成a、b两束单色光射出．对于a、b两束单色光下列说法正确的是（　　）‎ A．单色光a频率较小 B．单色光a穿过玻璃砖的时间较长 C．分别用单色光a、b在同一装置中做双缝干涉实验，a光的条纹间距小 D．若它们都从玻璃射向空气，a光发生全反射的临界角比b光的小 4、如图所示，P、Q是两种透明材料制成的两块直角梯形的棱镜，叠合在一起组成一个长方体．某单色光沿与P的上表面成θ角的方向斜射向P，其折射光线正好垂直通过两棱镜的界面．已知材料的折射率nP＜nQ，则下列说法正确的是（　　）‎ A．一定没有光线从Q的下表面射出 B．从Q的下表面射出的光线一定与入射到P的上表面的光线平行 C．如果光线从Q的下表面射出，出射光线与下表面所夹的锐角一定大于θ D．如果光线从Q的下表面射出，出射光线与下表面所夹的锐角一定小于θ ‎ 5、如图所示，O1O2是半圆柱形玻璃体的对称面和纸面的交线，A、B是关于O1O2轴等距且平行的两束不同单色细光束，从玻璃体右方射出后的光路图如图所示．MN是垂直于O1O2放置的光屏，沿O1O2方向不断左右移动光屏，可在光屏上得到一个光斑P，根据该光路图，下列说法正确的是（　　）‎ ‎　‎ A．‎ 该玻璃体对A光的折射率比对B光的折射率小 ‎　‎ B．‎ 在真空中，A光的波长比B光的波长长 ‎　‎ C．‎ 在该玻璃体中，A光比B光的速度大 ‎　‎ D．‎ A光的频率比B光的频率高 ‎　‎ E．‎ A光从空气进入该玻璃体后，其频率变高 ‎6、如图所示，一束光沿半径方向射向一块半圆柱形玻璃砖，在玻璃砖底面上的入射角为θ，经折射后射出a、b两束光线.则(　 　) ‎ A. 在玻璃中，a光的传播速度小于b光的传播速度 B. 在真空中，a光的波长小于b光的波长 C. 玻璃砖对a光的折射率小于对b光的折射率 D. 若改变光束的入射方向使θ角逐渐变大，则折射光线a首先消失 E. 在玻璃中，a光与b光的传播的时间相等 7、如图所示，△ABC为一直角三棱镜的截面，其顶角∠BAC = 30°，AB边的长度为L，P为垂直于直线BCD的光屏，P屏到C的距离为L。一宽度也为L的平行单色光束垂直射向AB面，在屏上形成一条宽度等于的光带，已知光速为c，求：‎ ‎(i)棱镜的折射率；‎ ‎(ii)沿BC边入射的光线从照射到玻璃砖到射到屏P上所用的时间。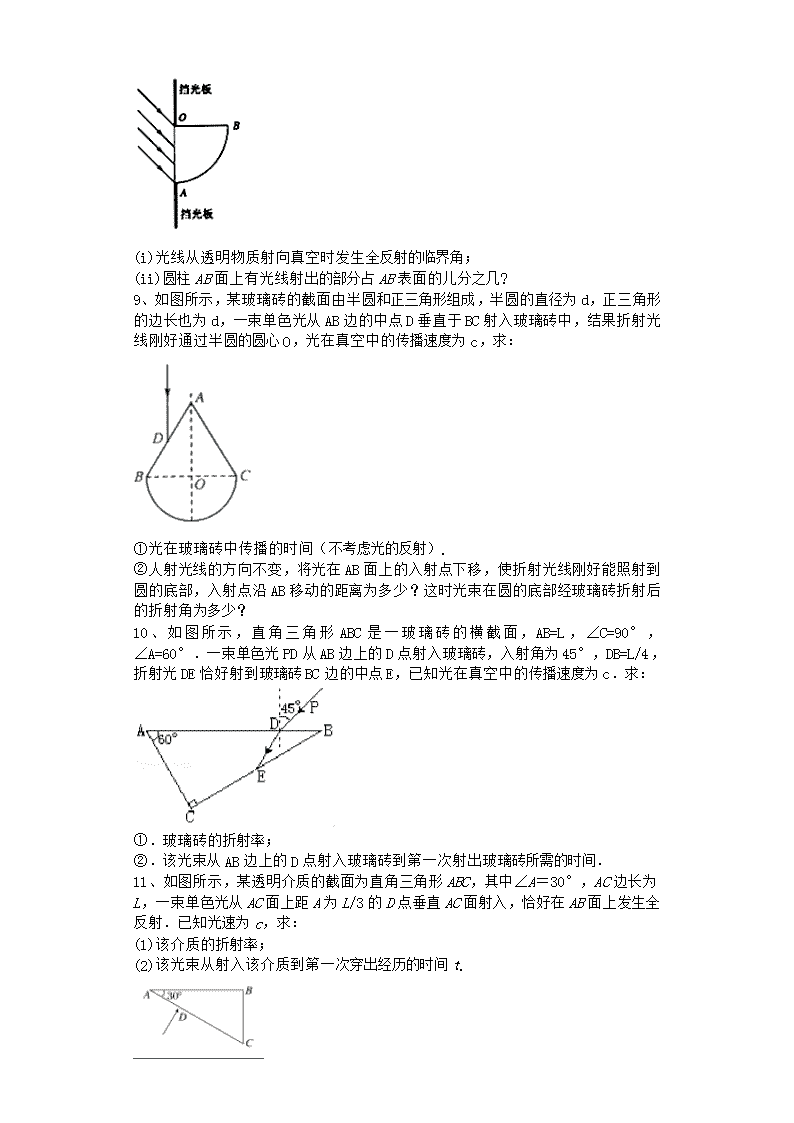‎ ‎8、如图所示，AOB是由某种透明物质制成的柱体的横截面(O为圆心)，其折射率为。今有一束平行光以的入射角射向柱体的OA平面，这些光线中有一部分不能从柱体的AB面上射出，假设凡射到OB面的光线全部被吸收，且不考虑OA面的反射，求：‎ ‎(i)光线从透明物质射向真空时发生全反射的临界角；‎ ‎(ii)圆柱AB面上有光线射出的部分占AB表面的儿分之几?‎ ‎9、如图所示，某玻璃砖的截面由半圆和正三角形组成，半圆的直径为d，正三角形的边长也为d，一束单色光从AB边的中点D垂直于BC射入玻璃砖中，结果折射光线刚好通过半圆的圆心O，光在真空中的传播速度为c，求：‎ ‎①光在玻璃砖中传播的时间（不考虑光的反射）.‎ ‎②人射光线的方向不变，将光在AB面上的入射点下移，使折射光线刚好能照射到圆的底部，入射点沿AB移动的距离为多少？这时光束在圆的底部经玻璃砖折射后的折射角为多少？‎ ‎10、如图所示，直角三角形ABC是一玻璃砖的横截面，AB=L，∠C=90°，∠A=60°．一束单色光PD从AB边上的D点射入玻璃砖，入射角为45°，DB=L/4，折射光DE恰好射到玻璃砖BC边的中点E，已知光在真空中的传播速度为c．求：‎ ‎①．玻璃砖的折射率；‎ ‎②．该光束从AB边上的D点射入玻璃砖到第一次射出玻璃砖所需的时间．‎ ‎11、如图所示，某透明介质的截面为直角三角形ABC，其中∠A＝30°，AC边长为L，一束单色光从AC面上距A为L/3的D点垂直AC面射入，恰好在AB面上发生全反射．已知光速为c，求：‎ ‎(1)该介质的折射率；‎ ‎(2)该光束从射入该介质到第一次穿出经历的时间t.‎ ‎12、一个半圆柱形玻璃砖，其横截面是半径为R的半圆，AB为半圆的直径，O为圆心，如图所示。一束足够宽的平行光垂直射向玻璃砖的下表面，光线到达上表面后，从该表面射出的光线在玻璃砖横截面上平行AB的宽度只有R。‎ ‎（Ⅰ）玻璃的折射率n为多少？‎ ‎（Ⅱ）一细束光线在O点左侧与O相距处垂直于AB从下方入射，不考虑AB面的反射光，求此光线从玻璃砖射出点的位置。 13、如图所示，横截面（纸面）为△ABC的三棱镜置于空气中，顶角∠A=60°．纸面内一细光束以入射角i射入AB面，直接到达AC面并射出，光束在通过三棱镜时出射光与入射光的夹角为φ（偏向角）．改变入射角i，当i=i0时，从AC面射出的光束的折射角也为i0，理论计算表明在此条件下偏向角有最小值φ0=30°．求三棱镜的折射率n．‎ ‎ 14、如图所示，一直角三棱镜放置在真空中，其截面三角形的斜边BC的长度为d，一束单色光从AB侧面的中点垂直AB入射．若三棱镜的折射率为，∠C=30°，单色光在真空中的传播速度为c，求：‎ ‎①该单色光第一次从棱镜射入真空时的折射角；‎ ‎②该单色光从进入棱镜到第一次从棱镜射出所经历的时间． 15、一束单色光斜着射向并穿过一厚度为d的玻璃砖．已知该玻璃砖对单色光的折射率为n，单色光的入射角为α光在真空中的传播速度为C．求：‎ ‎（1）若入射角α=60°，且已知n=．求该色光经玻璃砖上表面折射后的折射角；‎ ‎（2）该色光穿过玻璃砖所用的时间与入射角α和折射率n的关系．‎ ‎ 16、如图所示，一个半径为R、折射率为 的透明玻璃半球体，O为球心，轴线OA水平且与半球体的左边界垂直，位于轴线上O点左侧处的点光源S发出一束与OA夹角θ=60°光线射向半球体；已知光在真空中传播的速度为c，求：光线第一次从玻璃半球体出射时的方向以及光线在玻璃半球内传播的时间.‎ ‎ 17、一半圆柱形透明物体横截面如图所示，底面AOB镀银（图中粗线），O表示半圆截面的圆心，一束光线在横截面内从M点入射，经过AB面反射后从N点射出．已知光线在M点入射角为30°，∠MOA=60°，∠NOB=30°．求 ‎（ⅰ）光线在M点的折射角；‎ ‎（ⅱ）透明物体的折射率．‎ ‎ 18、如图所示，一个半径为R的透明球体放置在水平面上，一束蓝光从A点沿水平方向射入球体后经B点射出，最后射到水平面上的C点．已知OA=R，该球体对蓝光的折射率为．则：‎ ‎①它从球面射出时的出射角β为多少？‎ ‎②若光在真空中的传播速度为c，那么，请推导出光从A点传播到C点所需时间t的表达式（用c，R表示）‎ ‎ 　‎ ‎19、‎ 如图所示的装置可用来测定水的折射率。当圆柱形容器内未装水时，从A点沿AB方向能看到对边上的点E；当容器内装满水时，仍沿AB方向看去，恰好看到底面直径CD上的点D。测得容器直径CD =12 cm，高BC =16 cm，DE = 7 cm。已知光在真空中的传播速度为c = 3.0×108 m/s，求：‎ ‎①水的折射率n；‎ ‎②光在水中的传播速度v。‎ ‎20、半径为R的球体放置在水平面上，球体由折射率为的透明材料制成，现有一束位于过球心O的竖直平面内的光线，平行于桌面射到球体表面上，折射入球体后再从竖直表面射出，如图所示．已知入射光线与桌面的距离为，光在真空中的传播速度为c，求：出射光线在桌面上的落点M和O点之间的距离。‎ ‎ ‎ 参考答案 ‎1、答案：B ‎【考点】光的折射定律 ‎【分析】光只有从光密介质进入光疏介质时才可能发生全反射．光线肯定能从ab面进入玻璃板，根据折射定律求出折射角为30°．根据光路可逆性原理判断可知，光线肯定能从cd面射出玻璃板且折射角为60°．‎ ‎【解答】解：A、B、光从空气射到平行玻璃板上表面时，不可能发生全反射，一定能从ab面进入玻璃板．由n==，得折射角为r=30°．故A错误，B正确；‎ C、D、由几何知识可知，光线射到cd面上入射角等于30°，根据光路可逆性原理判断可知，光线在cd面上不可能发生全反射，肯定能从cd面射出玻璃板且折射角为60°．故C错误，D错误．‎ 故选：B．‎ 本题关键要抓住全反射的必要条件：光从光密介质进入光疏介质，以及光路可逆性原理，分析光线能否发生全反射． 2、答案：A ‎【考点】光的折射定律 ‎【分析】以大头针末端为研究对象，只要从大头针末端发出的光线射到薄板边缘界面处能够发生全反射，就从液面上看不到大头针，作出光路图，根据全反射的临界角公式求解液体的折射率．‎ ‎【解答】解：要在液面上各处均看不到大头针，要求光线射到薄板边缘界面处时恰好发生全反射，设临界角为C．‎ 由临界角与折射率的关系得：sinC=①‎ 由几何关系得：sinC===②‎ 联立①②式可得：n=‎ 故选：A 本题的关键要掌握全反射的条件和临界角的公式，要能画出光路图是解决此类问题的关键．同时注意几何知识的应用． 3、答案：A ‎【考点】光的折射定律 ‎【分析】由图看出，玻璃砖对b光的偏折角较大，b光的折射率较大，频率较大，波长短．由v=分析光在玻璃砖中传播速度关系，即可判断时间关系．折射率越大，波长越短，干涉条纹间距越小．由sinC=分析临界角的大小．‎ ‎【解答】解：A、由图知，玻璃砖对a光的偏折角较小，由折射定律n=得知，玻璃对a光的折射率较小，其频率较小．故A正确．‎ B、玻璃对a光的折射率较小，由v=分析得知，a光在玻璃砖中速度较大，传播时间较短．故B错误．‎ C、玻璃对a光的折射率较小，a光的波长较长，而干涉条纹的间距与波长成正比，则知，a光干涉条纹的间距较大．故C错误．‎ D、由sinC=分析得知，b光的折射率大，则临界角较小，故D错误．‎ 故选：A 本题运用折射定律n=分析折射率的大小是关键，再根据频率、波长、临界角与折射率的关系即可分析． 4、答案：D A、B光线正好垂直通过两棱镜的界面，沿直线射到Q的下表面，由于入射角与临界角关系不清楚，光线在Q的下表面可能发生全反射，不从 Q的下表面射出，也可能不发生全反射，从Q的下表面射出．故A、B错误． C、D如果光线从Q的下表面射出，光路如图． 根据折射定律有： 由几何知识知，r1=i2， 由题，nP＜nQ，则得r2＞i1 根据几何知识得：α＜θ．故C错误，D正确．‎ ‎5、答案：ABC． 考点： 光的折射定律．‎ 分析： 根据光线的偏折程度比较a、b两光的折射率，根据v=比较光在介质中的传播速度，根据光的频率，结合光子能量公式E=hγ分析光子能量的大小．由c=λγ比较波长的大小．‎ 解答： 解：A、B、D、B光的偏折程度比A光大，则B光的折射率大于A光的折射率，说明B光的频率较大，由c=λγ知，A光的波长较长，故A、B正确D错误；‎ C、根据v=得，A光的折射率较小，则A光在玻璃砖中的速度较大．故C正确．‎ E、光由一种介质进入另一种介质时频率不变，故E错误．‎ 故选：ABC．‎ 点评： 解决本题的突破口在于通过光的偏折程度比较光的折射率，知道折射率、频率、波长以及光在介质中的速度等大小关系． 6、答案：ABD 通过光路图可看出，折射后a光的偏折程度大于b光的偏折程度，玻璃砖对a光的折射率大于b光的折射率，故C错误；a光的频率大于b光的频率，波长小于b光的波长，故B正确；由知，在玻璃中，a光的传播速度小于b光的传播速度，故A正确；入射角增大时，折射率大的光线首先发生全反射，a光首先消失，故D正确.；由知，在玻璃中，a光的传播速度小于b光的传播速度，t=R/v，故F错误。所以ABD正确，CF错误。 7、答案：(i)平行光束经棱镜折射后的出射光束仍是平行光束，如图所示。图中θ1、θ2为AC面上入射角和折射角，根据折射定律，有nsin θ1 = sin θ2‎ 设出射光线与水平方向成α角，则θ2 = θ1 + α 而AC1 = BC = ABtan∠BAC 可得，解得α = 30°‎ 因θ1 = 30°，则有θ2 = 60°‎ 因此n ‎(ii)由上图可知，光线在玻璃中传播时间，而在空气中传播时间 因此所用的时间。 8、答案：(i)由公式 得到临界角为：‎ ‎(ii)从O点射入的光线，折射角为r，根据折射定律有：‎ 解得到：‎ 设从某位置P入射的光线，折射到AB弧面上Q点时，入射角恰等于临界角C ‎△PQO中 所以有射出光线的区域对应的圆心角为：‎ 有射出光线的部分占AB面的比例为 ‎ 9、答案：解：①由几何关系可知，光在AB面上的入射角为60°，折射角为30°(1分）‎ 根据折射率公式有n=（2分）‎ 由几何关系可知，光在玻璃砖中传播的路程s=d(1分）‎ 光在玻璃砖中传播的时间t= (1分）‎ ‎②由几何关系可知（1分）‎ 求得 (1分）‎ 因此入射点没AB移动的距离Δs=AE-AD=（1分）‎ 由几何关系可知，光线在玻璃砖底部的入射角为30°，根据光路可逆可知，光线在玻璃砖底部的折射角为60°（2分） 10、答案：（1） （2） ‎ ‎①．作出光路图，如图所示 ‎ 过E点的法线是三角形的中位线，由几何关系可知△DEB为等腰三角形，DE=DB=‎ 由几何知识可知光在AB边折射时折射角为 r=30°， 所以玻璃砖的折射率为 ②．设临界角为θ，有sinθ=，可解得 θ=45° 由光路图及几何知识可判断，光在BC边上的入射角为60°，大于临界角，则光在BC边上发生全反射；光在AC边的入射角为30°，小于临界角，所以光从AC第一次射出玻璃砖， 根据几何知识可知 EF=, 则光束从AB边射入玻璃砖到第一次射出玻璃砖所需要的时间为 而 ，可解得： ‎ 解决本题关键是作出光路图，再运用几何知识求解入射角折射角，要掌握几何光学常用的三个规律：折射定律 、临界角公式sinC=和光速公式． 11、答案：(1)2(2) ‎ 试题分析：(i)由于光线垂直于AC面射入，故光线在AB面上的入射角为30°，由题意知，光线恰好在AB面上发生全反射，由全反射条件可求得：n＝解得n＝2。‎ ‎(ii)由图可知，DF＝ADtan 30°＝‎ FE＝2DF＝, EG＝ECcos 30°＝‎ 故光在介质中的传播距离为：s＝DF＋FE＋EG＝‎ 光在该介质中的传播速度：光在介质中的传播时间：。‎ 考点：主要考查光的全反射。 12、答案：（Ⅰ）；（Ⅱ）O点右侧 试题分析：（Ⅰ）设在O点左侧从E点射入的光线，进入玻璃砖后在上表而的入射角恰好等于全反射的临界角θ，则OE区域的入射光线经上表而折射后都能从玻璃砖射出，如图，由全反射条件有 ‎ ①‎ 由几何关系有OE＝Rsinθ ②‎ 由对称性可知， ③‎ 联立①②③式，代入已知数据得：n＝ ④‎ ‎（Ⅱ）设光线在距O点的C点射入后，在上表面的入射角为α，由几何关系及①式和已知条件得：‎ α＝60°＞θ ⑤‎ 光线在玻璃砖内会发生三次全反射，最后由G点射出，如图，由反射定律和几何关系得：‎ ‎⑥‎ 射到G点的光有一部分被反射，沿原路返回到达C点射出。‎ 考点：光的折射定律；全反射 ‎【名师名师点评】本题考查了全反射定律以及反射定律的应用，正确作出光路图，灵活运用几何知识求解是关键；记住临界角的求解公式及发生全反射的条件． 13、答案：三棱镜的折射率n为．‎ ‎【考点】光的折射定律．‎ ‎【专题】光的折射专题．‎ ‎【分析】画出光路图，根据折射定律对AB面和AC面分别列式，再结合几何关系求解．‎ ‎【解答】解：设光束在AB面的折射角为α，由折射定律： ①‎ 设光束在AC面的入射角为β，由折射定律： ②‎ 由几何关系：α+β=60° ③‎ ‎ φ0=（i0﹣α）+（i0﹣β）④‎ 联立解得：‎ 答：三棱镜的折射率n为．‎ 本题是几何光学问题，作出光路图是解答的基础，关键能灵活运用数学知识求出折射角，并能掌握折射定律． 14、答案：①该单色光第一次从棱镜射入真空时的折射角是45°；‎ ‎②该单色光从进入棱镜到第一次从棱镜射出所经历的时间是． 【考点】光的折射定律 ‎【分析】①画出光路图，判断光线在AB面和BC面上能否发生全反射，由几何知识求出光线第一次射入空气时的入射角，由折射定律求解折射角；‎ ‎②根据几何关系求出光线在玻璃砖内通过的路程，由运动学知识求解时间．‎ ‎【解答】解：①画出该单色光在三棱镜中传播的光路图如图所示．‎ 当光线到达三棱镜的BC边时，因∠C=30°，由几何关系可知α=60°‎ 又因为三棱镜的折射率n=，所以光发生全反射的临界角为45°‎ 因α=60°，所以该单色光在BC边发生全反射．‎ 当该单色光到达三棱镜的AC边时，由几何关系可知，其入射角为β=30°‎ 设其折射角为γ，则由折射定律n=可得：γ=45°‎ ‎②因为截面三角形的斜边BC的长度为d，D为AB边的中点，∠C=30°，由几何关系可知=‎ 因为α=60°，所以∠CEF=30°，又∠C=30°，由几何关系可知=‎ 该单色光在三棱镜中的传播速度为v==‎ 所以单色光从进入棱镜到第一次从棱镜射出所经历的时间t=‎ 代入数据可解得：t=‎ 答：①该单色光第一次从棱镜射入真空时的折射角是45°；‎ ‎②该单色光从进入棱镜到第一次从棱镜射出所经历的时间是．‎ 本题是几何光学问题，做这类题目，一般首先要正确画出光路图，当光线从介质射入空气时要考虑能否发生全反射，要能灵活运用几何知识帮助我们分析角的大小． 15、答案：（1）若入射角α=60°，且已知n=．该色光经玻璃砖上表面折射后的折射角为30°；‎ ‎（2）该色光穿过玻璃砖所用的时间与入射角α和折射率n的关系t=． 考点:光的折射定律．‎ 专题:光的折射专题．‎ 分析:Ⅰ、已知入射角，由折射定律n=求解折射角．‎ Ⅱ、由几何知识求出光透过玻璃所走的路程为s=，光在玻璃中的速度为v=，时间为t=．‎ 解答:解：（1）设该色光的折射角θ，根据折射定律：‎ ‎=n 得：θ=30°‎ ‎（2）．设光透过玻璃所走路程为s，所用时间为t，则：‎ s=‎ 而v=‎ t=‎ 得：t=‎ 答：（1）若入射角α=60°，且已知n=．该色光经玻璃砖上表面折射后的折射角为30°；‎ ‎（2）该色光穿过玻璃砖所用的时间与入射角α和折射率n的关系t=．‎ 点评:本题是折射定律n=、光在介质中速度公式v=以及几何知识的综合应用 16、答案：出射光线CD方向与OA平行； 试题分析：作如图所示的光路图 ‎ ①‎ ‎ ② α=30o ③‎ 在ΔOBC中 ④ β=30o ⑤‎ ‎ ⑥ γ=60o ⑦ 即出射光线CD方向与OA平行 光在玻璃半球体中传播的距离 ⑧ 速度 ⑨ ⑩‎ 考点：光的折射定律.‎ ‎17、答案：（ⅰ）光线在M点的折射角为15°．‎ ‎（ⅱ）透明物体的折射率为 ‎【考点】光的折射定律 ‎【分析】（ⅰ）作出光路图，根据几何关系求出光线在M点的折射角．‎ ‎（ⅱ）根据折射角，通过折射定律求出透明物体的折射率．‎ ‎【解答】解：（ⅰ）如图，透明物体内部的光路为折线MPN，Q、M点相对于底面EF对称，Q、P和N三点共线 设在M点处，光的入射角为i，折射角为r，∠OMQ=α，∠PNF=β．根据题意有 α=30° ①‎ 由几何关系得，∠PNO=∠PQO=r，于是 β+r=60°②‎ 且α+r=β ③‎ 由①②③式得：r=15°④‎ ‎（ⅱ）根据折射率公式有 sini=nsinr ⑤‎ 由④⑤式得：n=⑥‎ 答：‎ ‎（ⅰ）光线在M点的折射角为15°．‎ ‎（ⅱ）透明物体的折射率为．‎ 本题主要考查光的折射和反射，掌握折射定律，本题对数学几何能力的要求较高． 18、答案：①它从球面射出时的出射角β为60°．‎ ‎②光从A点传播到C点所需时间t的表达式是． 考点： 光的折射定律．‎ 专题： 光的折射专题．‎ 分析： ①首先根据几何关系得出光线在B点时的入射角为30°由折射定律即可求出折射角β的大小；‎ ‎②由几何关系求出光在圆柱体中通过路程s，光在圆柱体中速度为v=，再由t=求解时间t．‎ 解答： 解：①设入射角为α，由几何关系可知：sinα==，α=30°‎ 由n=‎ 可得：sinβ=nsinα=×sin30°=‎ 所以：β=60° ‎ ‎②光在球体中的传播速度 v==‎ ‎ AB=R 则光从A传到B的时间 t1==‎ BC=R，则光从B传到C的时间 t2==‎ 故光从A点传播到C点所需时间 t=t1+t2=‎ 答：①它从球面射出时的出射角β为60°．‎ ‎②光从A点传播到C点所需时间t的表达式是．‎ 点评： 本题要熟练掌握光的折射定律的内容：入射光线、折射光线、法线在同一平面内，入射光线、折射光线分居法线两侧，入射角的正弦值与折射角的正弦值成正比．并要知道各种不同色光折射率的大小关系，即可轻松解决此类问题． ‎ ‎19、答案：①做出光路图，设入射角为i、折射角为r，则 则sin i = 0.8‎ 则sin r = 0.6 ‎ 折射率。‎ ‎②由可得光在水中的速度。 20、答案：R/3 设入射光线与1/4球体的交点为C，连接OC，OC为入射点的法线。‎ 因此，图中的角α为入射角，过C点作球体水平表面的垂线，垂足为B，依题意∠COB=α 设光线在C点的折射角为β，有折射定律可得：联立解得β=30°‎ ‎.....................‎ 因此 解得 ‎