2020年高二物理下学期期末模拟试卷及答案(九) 32页

第 1页（共 32页） 2020 年高二物理下学期期末模拟试卷及答案（九） 一、选择题（ 1-8 小题为单选； 9-12 题为多选题．每小题 4 分） 1．下列有关物理知识的说法中正确的是（ ） A．光能发生偏振现象说明光波是纵波 B．均匀变化的电场能够产生均匀变化的磁场 C．某人在速度为光速的 0.5 倍的飞行器上打开一光源，光源发出的 光相对于地面的速度为 1.5 倍光速 D．一切高温物体都能发射紫外线，紫外线能杀死多种细菌，还有助 于人体合成维生素 D 2．某同学漂浮在海面上，虽然水面波正平稳地以 1.5m/s的速率向着 海滩传播， 但他并不向海滩靠近． 该同学发现从第 1 个波峰到第 9 个 波峰通过身下的时间间隔为 16s．下列说法正确的是（ ） A．该水面波的频率为 2 Hz B．该水面波的波长为 3 m C．水面波没有将该同学推向岸边，是因为波传播时能量不会传递出 去 D．水面波没有将该同学推向岸边，是因为该同学太重，水波能量太 小 3．已知磁敏电阻在没有磁场时电阻很小，有磁场时电阻变大，并且 磁场越强电阻值越大． 为探测有无磁场， 利用磁敏电阻作为传感器设 计了如图所示的电路， 电源的电动势 E 和内阻 r 不变， 在没有磁场时 第 2页（共 32页） 调节变阻器 R 使电灯 L 正常发光．若探测装置从无磁场区进入强磁 场区，则（ ） A．电灯 L 亮度不变 B．电灯 L 亮度变暗 C．电流表的示数减小 D．电流表的示数增大 4．一交流发电机匀速转动时，其交变电动势 e=10sin（50πt）V，则 下列说法正确的是（ ） A．在 t=0 时，线圈中的磁通量为 0 B．该交流发电机线圈的转速为 25r/s C．若加在标有 “10V 20W”的灯泡的两端，灯泡能正常发光 D．若线圈的转速加倍，则交变电压的最大值、有效值增大一倍而频 率不变 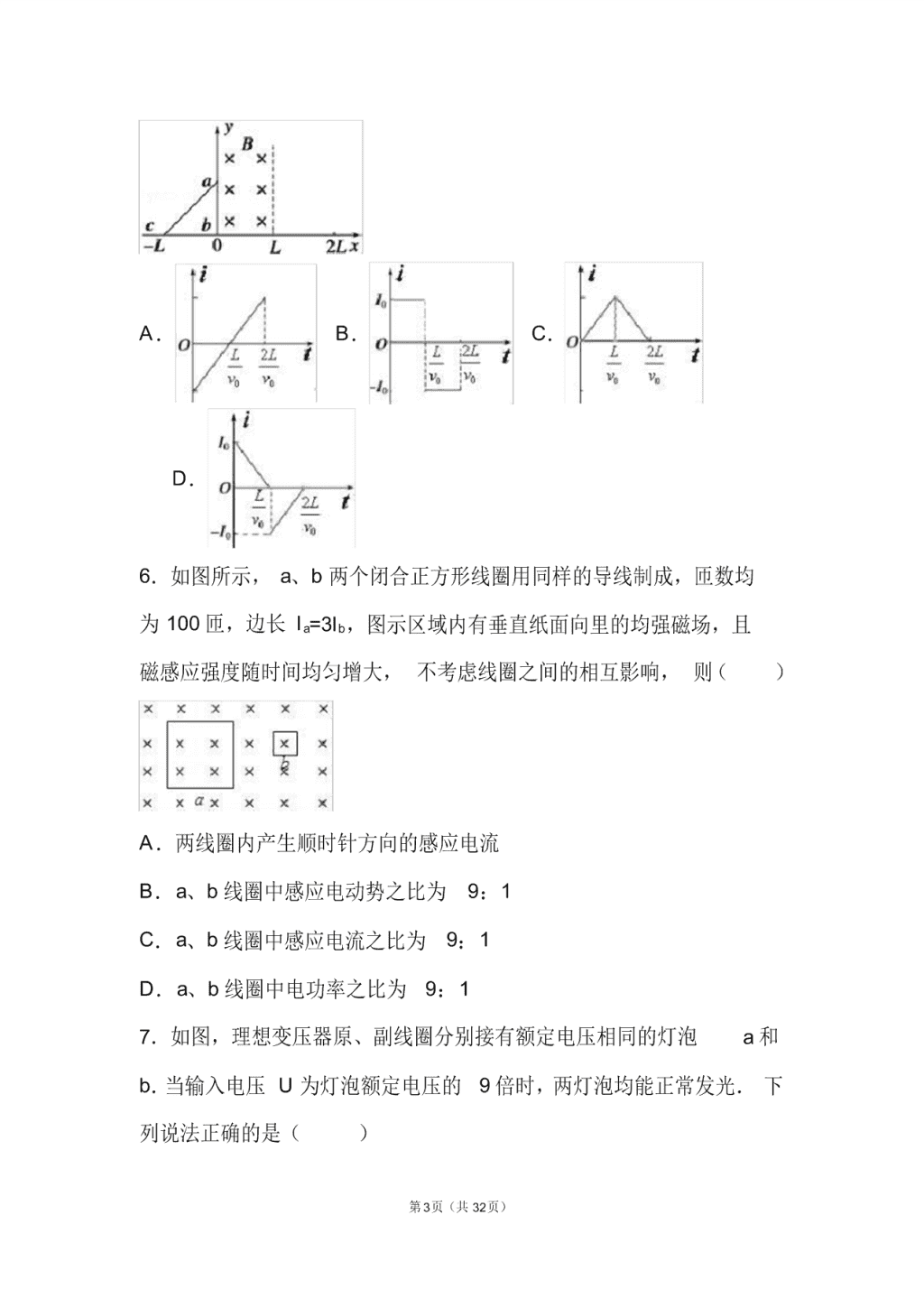5．如图所示，在 0≤x≤L 的区域内存在着匀强磁场，磁场方向垂直 于 xOy 坐标系平面（纸面）向里．具有一定电阻的等腰直角三角形 线框 abc位于 xOy 坐标系平面内，线框的 ab 边与 y 轴重合， bc 边长 为 L．设线框从 t=0 时刻起在外力作用下由静止开始沿 x 轴正方向做 匀速运动，则线框中的感应电流 i（取逆时针方向的电流为正）随时 间 t 变化的函数图象可能是图中的（ ） 第 3页（共 32页） A． B． C． D． 6．如图所示， a、b 两个闭合正方形线圈用同样的导线制成，匝数均 为 100 匝，边长 l a=3lb，图示区域内有垂直纸面向里的均强磁场，且 磁感应强度随时间均匀增大， 不考虑线圈之间的相互影响， 则 （ ） A．两线圈内产生顺时针方向的感应电流 B．a、b 线圈中感应电动势之比为 9：1 C．a、b 线圈中感应电流之比为 9：1 D．a、b 线圈中电功率之比为 9：1 7．如图，理想变压器原、副线圈分别接有额定电压相同的灯泡 a 和 b．当输入电压 U 为灯泡额定电压的 9 倍时， 两灯泡均能正常发光． 下 列说法正确的是（ ） 第 4页（共 32页） A．此时 a 和 b 的电流之比为 1：1 B．原、副线圈匝数之比为 9：1 C．原、副线圈匝数之比为 8：1 D．此时 a 和 b 的电功率之比为 8：1 8．一束复色光由空气射向一块平行平面玻璃砖，经折射后分成两束 单色光 a、b．已知 a 光的频率大于 b 光的频率． 下列哪个光路图可能 是正确的？（ ） A． B． C． D． 9．如图所示，在远距离输电过程中，若保持原线圈的输入功率不变， 下列说法正确的是（ ） A．升高 U1 会减小输电电流 I 2 B．升高 U1 会增大线路的功率损耗 C．升高 U1 会增大线路的电压损耗 D．升高 U1 会提高电能的利用率 10．简谐横波在均匀介质中沿直线传播， P、Q 是传播方向上相距 10m 的两质点，波先传到 P，当波传到 Q 开始计时， P、Q 两质点的振动 图象如图所示．则（ ） 第 5页（共 32页） A．质点 Q 开始振动的方向沿 y 轴正方向 B．该波从 P 传到 Q 的时间可能为 8 s C．该波的波长可能为 15 m D．该波的传播速度可能为 3 m/s 11．如图所示，竖直平行金属导轨 MN 、PQ 上端接有电阻 R，金属 杆质量为 m，跨在平行导轨上，垂直导轨平面的水平匀强磁场为 B， 不计 ab 与导轨电阻，不计摩擦，且 ab 与导轨接触良好．若 ab 杆在 竖直向上的外力 F 作用下匀速上升，则以下说法正确的是（ ） A．拉力 F 所做的功等于电阻 R 上产生的热量 B．杆 ab 克服安培力做的功等于电阻 R 上产生的热量 C．电流所做的功等于重力势能的增加量 D．拉力 F 与重力做功的代数和等于电阻 R 上产生的热量 12．如图，两条相距 l 的光滑平行金属导轨位于同一水平面内，其左 端接一阻值为 R 的电阻； 一与导轨垂直的金属棒置于两导轨上的 MN 之间；以 MN 为界，左侧有一面积为 S 均匀磁场，磁感应强度大小 B1=kt，式中 k 为常量；右侧还有一匀强磁场区域，磁感应强度大小 第 6页（共 32页） 为 B0，方向也垂直于纸面向里．零时刻起，金属棒在外加水平恒力 的作用下以速度 v0 向右匀速运动．金属棒与导轨的电阻均忽略不 计．下列说法正确的是（ ） A．t（＞0）时刻，穿过回路的磁通量为 B0lv0t B．t 时间内通过电阻的电量为 C．外力大小为 D．安培力的功率为 二、实验题（共 14 分） 13．利用双缝干涉测量光的波长实验中， 双缝间距 d=0.4mm，双缝到 光屏间的距离 l=0.5m，用某种单色光照射双缝得到干涉条纹如图所 示，分划板在图中 A 位置时游标卡尺读数为 11.1mm，分划板在图中 B 位置时游标卡尺读数如图所示，则： （1）分划板在图中 B 位置时游标卡尺读数 xB= mm； （2）该单色光的波长 λ= nm． 第 7页（共 32页） 14．硅光电池是一种可将光能转换为电能的器件， 某同学用图所示的 电路探究硅光电池的路端电压 U 与总电流 I 的关系，图中 R0 为定值 电阻且阻值的大小已知，电压表视为理想电压 表． （1）请根据图甲，将图乙中的实验器材连接成实验电路． （2）若电压表 V 2 的读数为 U0，则 I= ． （3）用一定强度的光照射硅光电池，调节滑动变阻器，通过测量得 到该电池的 U﹣I 曲线，见图丙．由此可知电池内阻 （选填 “是 ” 或 “不是 ”）常数，短路电流为 μA，电动势为 V． 三、计算题（本题共 4 小题，共 38 分，要求写出必要的文字说明、 主要的计算步骤和明确的答案） 15．一个水池内盛有某种透明液体，液体的深度为 H．在水池的底部 中央放一点光源 S，其中一条光线以 30°入射角射到液体与空气的界 面上，它的反射光线与折射光线的夹角为 105°，如图所示．求： ① 光在该液体中的传播速度大小； ② 液体表面被光源照亮区域的面积． 第 8页（共 32页） 16．一列简谐横波的波形如图所示， 实线表示 t1=0 时刻的波形图， 虚 线表示 t2=0.2s时刻的波形图．求： （1）若 0＜t2﹣t1＜ ，波的传播方向和周期 T； （2）若 T＜t2﹣t1＜2T，波速可能为多大． 17．如图，水平面（纸面）内间距为 l=0.5m 的平行金属导轨间接一 电阻，质量为 m=0.1kg、长度为也为 l，电阻为 r=0.2Ω的金属杆置于 导轨上， t=0 时，金属杆在水平向右、大小为 F=0.3N 的恒定拉力作 用下由静止开始运动， t=0.2s 时刻，金属杆进入磁感应强度大小为 B=0.8T、方向垂直于纸面向里的匀强磁场区域， 且在磁场中恰好能保 持匀速运动． 导轨的电阻均忽略不计， 杆与导轨始终保持垂直且接触 良好，两者之间的动摩擦因数为 μ=0.25．重力加速度大小为 g=10m/s2．求： （1）金属杆在磁场中运动时产生的电动势的大小； （2）电阻的阻值． 第 9页（共 32页） 18．如图所示，在一光滑的水平桌面上，放置一质量为 M ，宽为 L 的足够长 “ ”型框架，其 PQ 部分电阻为 R，其它部分的电阻不 计．PQ 与劲度系数为 k 的另一端固定的轻弹簧相连，开始弹簧处于 自然状态，框架静止．光滑弧形导轨宽也为 L，其下端与框架的 MN 刚好平滑接触（不连接） ．MN 右侧处于竖直向上的匀强磁场中，磁 感应强度为 B．现从距桌面高 h 处静止释放一质量为 m、电阻为 R 的 金属棒 ab，棒与框架之间的动摩擦因数为 μ，ab 运动到桌面时，受 到水平向右的恒力 F=3μmg 作用．当 ab 匀速时，框架已静止． （在上 述过程中弹簧一直在弹性限度内）问： （1）棒刚开始进入磁场的瞬间，框架的加速度为多大？ （2）棒匀速运动时的速度多大？ （3）若棒从滑上框架通过位移 s= 后开始匀速， 已知弹簧的弹性 势能的表达式为 kx 2（x 为弹簧的形变量） ，则在棒通过位移 s 的过 程中，回路中产生的电热为多少？ 第10页（共 32页） 参考答案与试题解析 一、选择题（ 1-8 小题为单选； 9-12 题为多选题．每小题 4 分） 1．下列有关物理知识的说法中正确的是（ ） A．光能发生偏振现象说明光波是纵波 B．均匀变化的电场能够产生均匀变化的磁场 C．某人在速度为光速的 0.5 倍的飞行器上打开一光源，光源发出的 光相对于地面的速度为 1.5 倍光速 D．一切高温物体都能发射紫外线，紫外线能杀死多种细菌，还有助 于人体合成维生素 D 【考点】 光的偏振；光的衍射；紫外线的荧光效应及其应用； * 长度 的相对性． 【分析】 光的偏振现象说明光是横波； 变化的电场产生磁场，均匀变化的电场产生恒定的磁场； 狭义相对论的两个基本假设： ① 物理规律在所有惯性系中都具有相同的形式． 这叫做相对性原理． ② 在所有的惯性系中，光在真空中的传播速率具有相同的值 C．这 叫光速不变原理．它告诉我们光（在真空中）的速度 c 是恒定的，它 不依赖于发光物体的运动速度． 【解答】 解： A、光的偏振现象说明光是横波，故 A 错误； 第11页（共 32页） B、根据电磁场理论，变化的电场产生磁场，均匀变化的电场产生恒 定的磁场，故 B 错误； C、根据爱因斯坦狭义相对论中光速不变原理，在不同的惯性参考系 中，一切物理规律都是相同的，真空的光速都是相同的，故 C 错误； D、一切高温物体都能发射紫外线，如弧光灯、太阳等；紫外线能杀 死多种细菌， 还有助于人体合成维生素 D，但过量的紫外线对人体是 有害的．故 D 正确． 故选： D 2．某同学漂浮在海面上，虽然水面波正平稳地以 1.5m/s的速率向着 海滩传播， 但他并不向海滩靠近． 该同学发现从第 1 个波峰到第 9 个 波峰通过身下的时间间隔为 16s．下列说法正确的是（ ） A．该水面波的频率为 2 Hz B．该水面波的波长为 3 m C．水面波没有将该同学推向岸边，是因为波传播时能量不会传递出 去 D．水面波没有将该同学推向岸边，是因为该同学太重，水波能量太 小 【考点】 波长、频率和波速的关系；横波的图象． 【分析】 首先根据题干中的条件，可计算出波的振动周期，再利用周 期与频率之间的关系，即可计算出波的频率，利用波速、周期、波长 之间的关系式 λ=vT 可求得波长．波是能量传递的一种方式． 第12页（共 32页） 【解答】 解：A、由第 1 个波峰到第 9 个波峰通过身下的时间间隔为 16s，可得知振动的周期 T 为：T= = s=2s，频率为： f= =0.5Hz， 故 A 错误． B、由公式 λ=vT，得 λ=1.5×2m=3m，故 B 正确． C、该同学只在自己的平衡位置附近做往复运动， 并不会 “随波逐流 ”， 但振动的能量和振动形式却会不断的向外传播，故 C、D 错误． 故选： B 3．已知磁敏电阻在没有磁场时电阻很小，有磁场时电阻变大，并且 磁场越强电阻值越大． 为探测有无磁场， 利用磁敏电阻作为传感器设 计了如图所示的电路， 电源的电动势 E 和内阻 r 不变， 在没有磁场时 调节变阻器 R 使电灯 L 正常发光．若探测装置从无磁场区进入强磁 场区，则（ ） A．电灯 L 亮度不变 B．电灯 L 亮度变暗 C．电流表的示数减小 D．电流表的示数增大 【考点】 闭合电路的欧姆定律． 【分析】 探测装置从无磁场区进入强磁场区时，电阻变大，则总电流 变小，根据闭合电路欧姆定律即可分析． 第13页（共 32页） 【解答】 解：探测装置从无磁场区进入强磁场区时，电阻变大，则电 路的总电阻变大，根据闭合电路欧姆定律可知，电路中总电流变小， 所以电流表的示数减小； 根据 U=E﹣Ir，可知 I 减小， U 增大，所以灯泡两段的电压增大，所 以电灯 L 变亮，故 ABD 错误， C 正确． 故选： C 4．一交流发电机匀速转动时，其交变电动势 e=10sin（50πt）V，则 下列说法正确的是（ ） A．在 t=0 时，线圈中的磁通量为 0 B．该交流发电机线圈的转速为 25r/s C．若加在标有 “10V 20W”的灯泡的两端，灯泡能正常发光 D．若线圈的转速加倍，则交变电压的最大值、有效值增大一倍而频 率不变 【考点】 正弦式电流的图象和三角函数表达式． 【分析】 首先明确交流电的描述，根据交流电的表达式，可知其最大 值，以及线圈转动的角速度等物理量，然后进一步求出其它物理量， 如有效值、周期、频率等． 【解答】 解： A、t=0 时，瞬时电动势为 e=10sin50πt（V）=0，则线 圈平面位于中性面，此时通过线圈的磁通量最大，故 A 错误． B、角速度 ω=50π，故周期 n= ，故 B 正确； 第14页（共 32页） C、所加交流电的有效值 ，故加在标有 “10V20W”的灯泡的 两端，灯泡能正常发光，灯泡不能正常发光，故 C 错误 D、转速加倍， 角速度加倍， 产生的感应电动势的最大值 Em=nBSω 加 倍，转速加倍，故 D 错误； 故选： B 5．如图所示，在 0≤x≤L 的区域内存在着匀强磁场，磁场方向垂直 于 xOy 坐标系平面（纸面）向里．具有一定电阻的等腰直角三角形 线框 abc位于 xOy 坐标系平面内，线框的 ab 边与 y 轴重合， bc 边长 为 L．设线框从 t=0 时刻起在外力作用下由静止开始沿 x 轴正方向做 匀速运动，则线框中的感应电流 i（取逆时针方向的电流为正）随时 间 t 变化的函数图象可能是图中的（ ） A． B． C． D． 【考点】 导体切割磁感线时的感应电动势；闭合电路的欧姆定律． 第15页（共 32页） 【分析】 线圈匀速穿过磁场区域时，开始过程 ab 边和 ac 边都切割磁 感线，切割的有效长度均匀减小， 线圈出磁场时， ac 边切割的有效长 度均匀减小． 根据右手定则判定感应电流的方向， 结合法拉第电磁感 应定律和欧姆定律分析感应电流的大小． 【解答】 解： t 在 0﹣ 内，根据右手定则可知线框中感应电流方向 为逆时针方向，即正方向， 有效的切割长度均匀减小，产生的感应电 动势均匀减小到 0，则感应电流均匀减小到 0； 在 ﹣ 内，根据右手定则可知线框中感应电流方向为顺时针方向， 即负方向， 有效的切割长度均匀减小， 产生的感应电动势均匀减小到 0，则感应电流均匀减小到 0；故 ABC 错误， D 正确． 故选： D 6．如图所示， a、b 两个闭合正方形线圈用同样的导线制成，匝数均 为 100 匝，边长 l a=3lb，图示区域内有垂直纸面向里的均强磁场，且 磁感应强度随时间均匀增大， 不考虑线圈之间的相互影响， 则 （ ） A．两线圈内产生顺时针方向的感应电流 B．a、b 线圈中感应电动势之比为 9：1 C．a、b 线圈中感应电流之比为 9：1 D．a、b 线圈中电功率之比为 9：1 【考点】 法拉第电磁感应定律；电功、电功率． 第16页（共 32页） 【分析】 根据楞次定律可求得电流方向； 根据法拉第电磁感应定律可 求得感应电动势； 根据电阻定律可分析电阻大小， 根据欧姆定律即可 明确电流大小；再根据功率公式即可明确功率之比． 【解答】 解：A、根据楞次定律可知，原磁场向里增大，则感应电流 的磁场与原磁场方向相反，因此感应电流为逆时针；故 A 错误； B、根据法拉第电磁感应定律可知， E= = ； 而 la=3lb； 因 此电动势之比为 9：1；故 B 正确； C、线圈中电阻 R=ρ ，而导线长度 L=n×4l；故电阻之比为： 3：1； 由欧姆定律可知， I= ；则电流之比为： 3：1； 故 C 错误； D、电功率 P= ，电动势之比为 9：1；电阻之比为 3：1；则电功率 之比为 27：1；故 D 错误； 故选： B． 7．如图，理想变压器原、副线圈分别接有额定电压相同的灯泡 a 和 b．当输入电压 U 为灯泡额定电压的 9 倍时， 两灯泡均能正常发光． 下 列说法正确的是（ ） A．此时 a 和 b 的电流之比为 1：1 B．原、副线圈匝数之比为 9：1 C．原、副线圈匝数之比为 8：1 D．此时 a 和 b 的电功率之比为 8：1 第17页（共 32页） 【考点】 导体切割磁感线时的感应电动势；电功、电功率． 【分析】 根据灯泡电压与输入电压的关系可确定接在线圈的输入端和 输出端的电压关系， 则可求得匝数之比； 根据变压器电流之间的关系 和功率公式可确定功率之比． 【解答】 解：ABC 、灯泡正常发光，则其电压均为额定电压，因为输 入电压 U 为灯泡额定电压的 9 倍，所以原线圈输入电压为灯泡额定 电压的 8 倍，输出电压等于灯泡的额定电压，可知，原副线圈匝数之 比为 = ，根据公式 = 得 a 和 b 的电流之比为 = ，故 AB 错误， C 正确． D、由于小灯泡两端的电压相等，所以根据公式 P=UI 可得，两者的 电功率之比为 1：8；故 D 错误； 故选： C 8．一束复色光由空气射向一块平行平面玻璃砖，经折射后分成两束 单色光 a、b．已知 a 光的频率大于 b 光的频率． 下列哪个光路图可能 是正确的？（ ） A． B． C． D． 【考点】 光的折射定律． 【分析】 光线经平行平面玻璃砖两次折射后，根据折射定律得到：出 射光线与入射光线平行．由题： a 光的频率大于 b 光的频率，则玻璃 砖对 a 光的折射率大于 b 光的折射率， 当入射角相同时， 由折射定律 第18页（共 32页） 分析折射角大小， 确定光线通过玻璃砖后侧向位移的大小， 再进行选 择． 【解答】解：光线经平行平面玻璃砖两次折射后，根据折射定律和光 路可逆性原理可知出射光线与入射光线平行． 据题： a 光的频率大于 b 光的频率，则玻璃砖对 a 光的折射率大于 b 光的折射率， 当入射角相同时， 由折射定律分析得知 a 的折射角小于 b 光的折射角，在玻璃砖内部， a 光在 b 光右侧，光线通过玻璃砖后 a 的侧向位移大．故 A 正确． 故选： A 9．如图所示，在远距离输电过程中，若保持原线圈的输入功率不变， 下列说法正确的是（ ） A．升高 U1 会减小输电电流 I 2 B．升高 U1 会增大线路的功率损耗 C．升高 U1 会增大线路的电压损耗 D．升高 U1 会提高电能的利用率 【考点】 远距离输电；电功、电功率． 【分析】 根据 P=UI 判断输电线上电流的变化， 结合 判 断功率损失和电压损失的变化． 结合损耗的功率判断电能利用率的变 化． 第19页（共 32页） 【解答】 解：A、输送功率不变，升高 U1，则升压变压器的输出电压 变大，根据 P=UI 知，输电线上的电流 I 2 减小．故 A 正确． B、因为升高 U1，输电线上的电流减小，根据 知，输电线上 的功率损耗减小．故 B 错误． C、因为升高 U1，输电线上的电流减小，根据△ U=IR 知，输电线上 的电压损失减小．故 C 错误． D、电能的利用率为 ，因为升高 U1，输电线上的电流减小，则 电能的利用率提高．故 D 正确． 故选： AD． 10．简谐横波在均匀介质中沿直线传播， P、Q 是传播方向上相距 10m 的两质点，波先传到 P，当波传到 Q 开始计时， P、Q 两质点的振动 图象如图所示．则（ ） A．质点 Q 开始振动的方向沿 y 轴正方向 B．该波从 P 传到 Q 的时间可能为 8 s C．该波的波长可能为 15 m D．该波的传播速度可能为 3 m/s 【考点】 波长、频率和波速的关系；横波的图象． 第20页（共 32页） 【分析】 根据图象的斜率分析 Q 点的起振方向．首先可从图中读出 波传播的周期，再几何其周期性的计算出从 P 传到 Q 的时间可能的 时间． 由 v= 结合波的周期， 利用 B 的中的可能时间， 可计算出可能的波 速．利用公式 λ=vT 分析可能的波长． 【解答】 解：A、根据振动图象的斜率表示速度，可知质点 Q 的起振 方向即 t=0 时刻的速度方向沿 y 轴正方向，故 A 正确． B、由题可知， 简谐横波的传播方向从 P 到 Q，由图可知， 周期为 T=6s， 质点 Q 的振动图象向左 4s、后与 P 点的振动重合，意味着 Q 点比 P 点振动滞后了 4s，即 P 传到 Q 的时间△ t 可能为 4s，同时由周期性可 知，从 P 传到 Q 的时间△ t 为（4+nT）s，n=0、1、2、3⋯，即△t=4s， 10s，16s⋯，不可能为 8s，故 B 错误． CD、由 v= ，考虑到波的周期性，当△ t=4s，10s，16s⋯时，速度 v 可能为 2.5m/s，1m/s，0.625m/s⋯，不可能为 3m/s． 由 λ=vT 可知，波长可能为 15m、6m、3.75m⋯，故 C 正确， D 错误． 故选： AC 11．如图所示，竖直平行金属导轨 MN 、PQ 上端接有电阻 R，金属 杆质量为 m，跨在平行导轨上，垂直导轨平面的水平匀强磁场为 B， 不计 ab 与导轨电阻，不计摩擦，且 ab 与导轨接触良好．若 ab 杆在 竖直向上的外力 F 作用下匀速上升，则以下说法正确的是（ ） 第21页（共 32页） A．拉力 F 所做的功等于电阻 R 上产生的热量 B．杆 ab 克服安培力做的功等于电阻 R 上产生的热量 C．电流所做的功等于重力势能的增加量 D．拉力 F 与重力做功的代数和等于电阻 R 上产生的热量 【考点】 导体切割磁感线时的感应电动势；闭合电路的欧姆定律；电 磁感应中的能量转化． 【分析】 ab 杆匀速上升时，动能不变，重力势能增加，整个回路的 内能增加，根据能量守恒进行分析． 【解答】 解：A 、根据能量守恒定律知，拉力 F 做的功等于重力势能 的增加量和电阻 R 上产生的热量之和．故 A 错误． B、根据功能关系知，杆 ab 克服安培力做功等于电阻 R 上产生的热 量．故 B 正确． C、安培力的大小与重力的大小不等，则电流做的功与重力做功大小 不等，即电流做功不等于重力势能的增加量．故 C 错误． D、根据动能定理知，拉力和重力做功等于克服安培力做功的大小， 克服安培力做功等于电阻 R 上的热量．故 D 正确． 故选 BD． 第22页（共 32页） 12．如图，两条相距 l 的光滑平行金属导轨位于同一水平面内，其左 端接一阻值为 R 的电阻； 一与导轨垂直的金属棒置于两导轨上的 MN 之间；以 MN 为界，左侧有一面积为 S 均匀磁场，磁感应强度大小 B1=kt，式中 k 为常量；右侧还有一匀强磁场区域，磁感应强度大小 为 B0，方向也垂直于纸面向里．零时刻起，金属棒在外加水平恒力 的作用下以速度 v0 向右匀速运动．金属棒与导轨的电阻均忽略不 计．下列说法正确的是（ ） A．t（＞0）时刻，穿过回路的磁通量为 B0lv0t B．t 时间内通过电阻的电量为 C．外力大小为 D．安培力的功率为 【考点】 导体切割磁感线时的感应电动势；闭合电路的欧姆定律；安 培力． 【分析】 根据磁通量的公式 Φ=BS，结合磁场方向，即可求解穿过回 路的总磁通量； 根据动生电动势与感生电动势公式， 求得线圈中的总 感应电动势， 再依据闭合电路欧姆定律求得感应电流， 再求得通过电 阻 R 的电量和金属棒所受的安培力，最后依据平衡条件，即可求解 水平恒力大小．由 P=Fv 求安培力的功率． 第23页（共 32页） 【解答】 解： A、根据题意可知， MN 左边的磁场方向与右边的磁场 方向相同，那么总磁通量即为两种情况磁通量之和， 则在时刻 t（t＞0）穿过回路的总磁通量为 Φ=Φ1+Φ2=ktS+B0v0tl=ktS+B0lv0t；故 A 错误． B、根据法拉第电磁感应定律得 E= ，结合闭合电路欧姆定律得 I= ，则 t 时间内通过电阻的电量为 q=I△t= = ，故 B 正确． C、依据法拉第电磁感应定律 E= 得，线圈中产生总感应电动势 E=E1+E2=kS+B0lv 0； 根据闭合电路欧姆定律得，线圈中产生感应电流大小为 I= = 那么金属棒所受的安培力大小 FA=B0Il= ； 根据平衡条件得，水平恒力大小等于安培力大小，即为 F= ．故 C 正确． D、安培力的功率等于外力的功率，为 P=Fv0= ，故 D 错误． 故选： BC 二、实验题（共 14 分） 13．利用双缝干涉测量光的波长实验中， 双缝间距 d=0.4mm，双缝到 光屏间的距离 l=0.5m，用某种单色光照射双缝得到干涉条纹如图所 第24页（共 32页） 示，分划板在图中 A 位置时游标卡尺读数为 11.1mm，分划板在图中 B 位置时游标卡尺读数如图所示，则： （1）分划板在图中 B 位置时游标卡尺读数 xB= 15.6 mm； （2）该单色光的波长 λ= 600 nm． 【考点】 双缝干涉的条纹间距与波长的关系． 【分析】 （1）游标卡尺的读数等于主尺读数加上游标读数， 不需估读． （2）根据 求出相邻两条纹的间距．根据双缝干涉条纹的 间距公式 得出波长 λ的表达式，以及求出波长的长度． 【解答】 解：（1）B 位置游标卡尺的主尺读数为 15mm，游标读数为 0.1×6mm=0.6mm，所以最终读数为 15.6mm． （2）A 位置游标卡尺的主尺读数为 11mm，游标读数为 0.1× 1mm=0.1mm，所以最终读数为 11.1mm． 所以： ． 根据双缝干涉条纹的间距公式 得： ．代入数据得：λ=6.0 ×10﹣7m=600nm． 故答案为： （1）15.6；（2）600 14．硅光电池是一种可将光能转换为电能的器件， 某同学用图所示的 电路探究硅光电池的路端电压 U 与总电流 I 的关系，图中 R0 为定值 第25页（共 32页） 电阻且阻值的大小已知，电压表视为理想电压 表． （1）请根据图甲，将图乙中的实验器材连接成实验电路． （2）若电压表 V 2 的读数为 U0，则 I= ． （3）用一定强度的光照射硅光电池，调节滑动变阻器，通过测量得 到该电池的 U﹣I 曲线， 见图丙． 由此可知电池内阻 不是 （选填 “是 ” 或 “不是 ”）常数，短路电流为 300 μA，电动势为 2.65 V． 【考点】 闭合电路的欧姆定律． 【分析】 （1）根据原理图可以画出实物图，注意正负极不要连反了． （2）根据欧姆定律求电流 （3）电源的 U﹣I 图象的斜率表示其内阻， 根据斜率的变化可以知道 内阻的变化情况， 图象与纵轴交点表示电动势， 与横轴交点表示短路 电流． 【解答】 解：（1）分析图甲所示实验原理图，根据原理图连接实物电 路图，如图所示． （2）根据欧姆定律 （3）在硅光电池的 U﹣I 图象，当 I=0，U=E，即 E=2.65V 第26页（共 32页） 图线斜率的绝对值表示内阻．斜率是变化的，即电池内阻不是常数， 路端电压为 0 时的电流为短路电流，由图知短路电流为 300μA 故答案为： （1）如图所示 （2） （3）不是 300 2.65 三、计算题（本题共 4 小题，共 38 分，要求写出必要的文字说明、 主要的计算步骤和明确的答案） 15．一个水池内盛有某种透明液体，液体的深度为 H．在水池的底部 中央放一点光源 S，其中一条光线以 30°入射角射到液体与空气的界 面上，它的反射光线与折射光线的夹角为 105°，如图所示．求： ① 光在该液体中的传播速度大小； ② 液体表面被光源照亮区域的面积． 【考点】 光的折射定律． 第27页（共 32页） 【分析】 ① 由题，已知入射角 i=30°，折射角 r=45°，根据折射定律 求解该液体的折射率，由公式 v= 求解光在该液体中的传播速度大 小； ② 当光恰好发生全反射，亮斑面积最大，由 sinc= 可求出临界角， 再由几何关系，可求出光斑面积． 【解答】 解： ① 由图知：入射角 i=30°折射角 r=45° 则得 n= = = 光在该液体中的传播速度大小 v= = m/s=2.12×108 m/s （2）若发生全反射，入射角 C 应满足 由 sinc= = 可得： C=45° 亮斑半： R=Htanc=H 亮斑面积： S=πH2 答： ① 光在该液体中的传播速度大小是 2.12×108 m/s； ② 液体表面被光源照亮区域的面积是 πH 2． 16．一列简谐横波的波形如图所示， 实线表示 t1=0 时刻的波形图， 虚 线表示 t2=0.2s时刻的波形图．求： （1）若 0＜t2﹣t1＜ ，波的传播方向和周期 T； （2）若 T＜t2﹣t1＜2T，波速可能为多大． 第28页（共 32页） 【考点】 波长、频率和波速的关系；横波的图象． 【分析】 （1）根据波的传播时间，结合波形图，即可确定波的传播方 向，再由时间与周期的关系，即可求解周期； （2）根据时间与周期的关系，确定波传播的距离，由 v= ，即可 求解波速． 【解答】 解：（1）若 t2﹣t1＜ ，根据波形的平移法可知波向右传播 且有（ t2﹣t1）= T，所以 T=4（t2﹣t1）=0.8s （2）若 2T＞t2﹣t1＞T，则有两种可能： ① 若波向右传播，波传播的距离为△ x=λ+ λ=8m+2m=10m 则 v= = m/s=50m/s ② 若波向左传播，波传播的距离为△ x=λ+ λ=8m+6m=14m 则 v= = m/s=70m/s 答： （1）若 0＜t2﹣t1＜ ，波的传播方向向右，周期 T 为 0.8； （2）若 T＜t2﹣t1＜2T，波速可能为 50m/s 或 70m/s． 17．如图，水平面（纸面）内间距为 l=0.5m 的平行金属导轨间接一 电阻，质量为 m=0.1kg、长度为也为 l，电阻为 r=0.2Ω的金属杆置于 导轨上， t=0 时，金属杆在水平向右、大小为 F=0.3N 的恒定拉力作 第29页（共 32页） 用下由静止开始运动， t=0.2s 时刻，金属杆进入磁感应强度大小为 B=0.8T、方向垂直于纸面向里的匀强磁场区域， 且在磁场中恰好能保 持匀速运动． 导轨的电阻均忽略不计， 杆与导轨始终保持垂直且接触 良好，两者之间的动摩擦因数为 μ=0.25．重力加速度大小为 g=10m/s2．求： （1）金属杆在磁场中运动时产生的电动势的大小； （2）电阻的阻值． 【考点】 导体切割磁感线时的感应电动势；闭合电路的欧姆定律． 【分析】 （1）根据牛顿第二定律和运动学公式求刚进入磁场时的速度， 再根据法拉第电磁感应定律求切割电动势； （2）进入磁场匀速运动受力平衡求出安培力，结合闭合电路欧姆定 律求电流，即可求电阻． 【解答】 解：（1）根据牛顿第二定律： F﹣μmg=ma 刚进磁场时的速度： v0=at 感应电动势为： E=Blv 0 解得： =0.04V； （2）匀速运动受力平衡： F=μmg+BIl 回路电流为： I= 得： = T=0.32Ω． 第30页（共 32页） 答：（1）金属杆在磁场中运动时产生的电动势的大小 0.04V； （2）电阻的阻值为 0.32Ω． 18．如图所示，在一光滑的水平桌面上，放置一质量为 M ，宽为 L 的足够长 “ ”型框架，其 PQ 部分电阻为 R，其它部分的电阻不 计．PQ 与劲度系数为 k 的另一端固定的轻弹簧相连，开始弹簧处于 自然状态，框架静止．光滑弧形导轨宽也为 L，其下端与框架的 MN 刚好平滑接触（不连接） ．MN 右侧处于竖直向上的匀强磁场中，磁 感应强度为 B．现从距桌面高 h 处静止释放一质量为 m、电阻为 R 的 金属棒 ab，棒与框架之间的动摩擦因数为 μ，ab 运动到桌面时，受 到水平向右的恒力 F=3μmg 作用．当 ab 匀速时，框架已静止． （在上 述过程中弹簧一直在弹性限度内）问： （1）棒刚开始进入磁场的瞬间，框架的加速度为多大？ （2）棒匀速运动时的速度多大？ （3）若棒从滑上框架通过位移 s= 后开始匀速， 已知弹簧的弹性 势能的表达式为 kx 2（x 为弹簧的形变量） ，则在棒通过位移 s 的过 程中，回路中产生的电热为多少？ 【考点】 导体切割磁感线时的感应电动势； 牛顿第二定律； 动能定理； 焦耳定律． 第31页（共 32页） 【分析】 （1）ab 运动的水平桌面上时的速度为 v，根据动能定理求解 速度大小，再根据牛顿第二定律求解加速度； （2）根据共点力的平衡条件求解棒匀速运动时的速度； （3）导体棒匀速运动时，根据共点力的平衡条件弹簧的压缩量；整 个过程中根据能量守恒定律求解回路中产生的电热． 【解答】 解：（1）ab 运动的水平桌面上时的速度为 v，根据动能定理 可得： ， 解得： v= ； 此时回路中的电流强度为： ， 根据牛顿第二定律可得： μmg+BIL=Ma ， 解得： a= ； （2）设棒匀速运动时的速度为 v′，根据共点力的平衡条件可得： F=μmg+ ， 将 F=3μmg 代入可得： v′= ； （3）导体棒匀速运动时， 根据共点力的平衡条件可得： F=BIL +μmg， 解得： BIL=2 μmg； 以框架为研究对象，根据胡克定律可得： kx=BIL +μmg=3μmg 解得： x= ； 设整个过程中产生的电热为 Q，根据能量守恒定律可得： ， 第32页（共 32页） 解得： Q=mgh ．