【物理】2020届一轮复习人教版 机械振动 课时作业 7页

第1讲　机械振动 ‎◎基础巩固练 ‎1．(多选)如图所示，图甲为以O点为平衡位置，在A、B两点间做简谐运动的弹簧振子，图乙为该弹簧振子的振动图象，由图可知下列说法中正确的是________。‎ A．在t＝0.2 s时，弹簧振子可能运动到B位置 B．在t＝0.1 s与t＝0.3 s两个时刻，弹簧振子的速度相反 C．从t＝0到t＝0.2 s的时间内，弹簧振子的动能持续地增加 D．在t＝0.2 s与t＝0.6 s两个时刻，弹簧振子的加速度相同 E．在t＝0.4 s和t＝0.8 s时弹簧振子动能最大 解析：　t＝0.2 s时，振子的位移为正的最大，但由于没有规定正方向，所以此时振子的位置可能在A点也可能在B点，A正确。t＝0.1 s时速度为正，t＝0.3 s时速度为负，两者方向相反，B正确。从t＝0到t＝0.2 s的时间内，弹簧振子远离平衡位置，速度减小，动能减小，C错。t＝0.2 s与t＝0.6 s两个时刻，位移大小相等，方向相反，故加速度大小相等，方向相反，D错。振子在平衡位置动能最大，E正确。‎ 答案：　ABE ‎2.‎ ‎(多选)(2018·福建漳州模拟)如图所示，弹簧下面挂一质量为m的物体，物体在竖直方向上做振幅为A的简谐运动，当物体振动到最高点时，弹簧正好为原长，弹簧在弹性限度内，则物体在振动过程中________。‎ A．弹簧的最大弹性势能等于2mgA B．弹簧的弹性势能和物体动能总和不变 C．物体在最低点时的加速度大小应为g D．物体在最低点时的弹力大小应为mg E．物体在最低点时的弹力大小应为2mg 解析：　因物体振动到最高点时，弹簧正好为原长，此时弹簧弹力等于零，物体的重力mg＝F回＝kA，当物体在最低点时，弹簧的弹性势能最大等于2mgA，A对；在最低点，由F回＝mg＝ma知，C对；由F弹－mg＝F回得F弹＝2mg，D错，E对；由能量守恒知，弹簧的弹性势能和物体的动能、重力势能三者的总和不变，B错。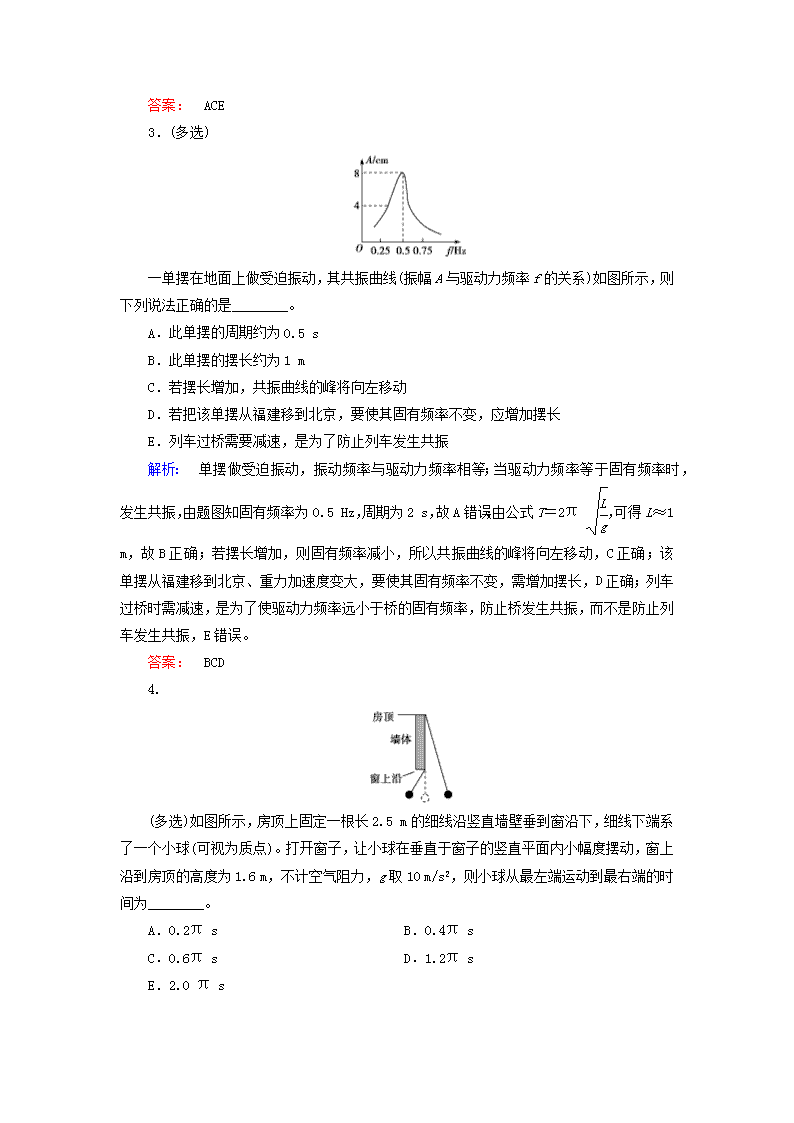‎ 答案：　ACE ‎3．(多选)‎ 一单摆在地面上做受迫振动，其共振曲线(振幅A与驱动力频率f的关系)如图所示，则下列说法正确的是________。‎ A．此单摆的周期约为0.5 s B．此单摆的摆长约为1 m C．若摆长增加，共振曲线的峰将向左移动 D．若把该单摆从福建移到北京，要使其固有频率不变，应增加摆长 E．列车过桥需要减速，是为了防止列车发生共振 解析：　单摆做受迫振动，振动频率与驱动力频率相等；当驱动力频率等于固有频率时，发生共振，由题图知固有频率为0.5 Hz，周期为2 s，故A错误；由公式T＝2π ，可得L≈1 m，故B正确；若摆长增加，则固有频率减小，所以共振曲线的峰将向左移动，C正确；该单摆从福建移到北京、重力加速度变大，要使其固有频率不变，需增加摆长，D正确；列车过桥时需减速，是为了使驱动力频率远小于桥的固有频率，防止桥发生共振，而不是防止列车发生共振，E错误。‎ 答案：　BCD ‎4.‎ ‎(多选)如图所示，房顶上固定一根长2.5 m的细线沿竖直墙壁垂到窗沿下，细线下端系了一个小球(可视为质点)。打开窗子，让小球在垂直于窗子的竖直平面内小幅度摆动，窗上沿到房顶的高度为1.6 m，不计空气阻力，g取10 m/s2，则小球从最左端运动到最右端的时间为________。‎ A．0.2π s　　　　　　　　　 B．0.4π s C．0.6π s D．1.2π s E．2.0 π s 解析：　小球的摆动可视为单摆运动，摆长为线长时对应的周期：T1＝2π ＝π s，摆长为线长减去墙体长时对应的周期T2＝2π ＝0.6π s，故小球从最左端到最右端所用的最短时间为t＝＝0.4π s，B、D、E正确。‎ 答案：　BDE ‎5.‎ ‎(多选)(2018·广东顺德一模)弹簧振子在光滑水平面上振动，其位移时间图象如图所示，则下列说法正确的是________。‎ A．10秒内振子的路程为2 m B．动能变化的周期为2.0 s C．在t＝0.5 s时，弹簧的弹力最大 D．在t＝1.0 s时，振子的速度反向 E．振动方程是x＝0.10sin πt(m)‎ 解析：　根据振动图象可知周期T＝2.0 s，振幅A＝10 cm，t＝10 s＝5T，一个周期通过的路程为4A，则10 s内通过的路程s＝5×4A＝20×10 cm＝200 cm＝2 m，故A正确；每次经过平衡位置动能最大，在最大位移处动能为0，在振子完成一个周期的时间内，动能完成2个周期的变化，故动能变化的周期为1 s，故B错误；t＝0.5 s时，振子处于最大位移处，弹簧的弹力最大，故C正确；在t＝0.5 s到t＝1.5 s时间内振子沿x负方向运动，在t＝0.1 s时，振子的速度未反向，故D错误；由振动图象知T＝2.0 s，角速度ω＝＝ rad/s＝π rad/s，振动方程x＝0.10sin πt(m)，故E正确。故选A、C、E。‎ 答案：　ACE ‎6．(2018·安徽合肥模拟)(1)在用单摆测定当地的重力加速度的实验中，除带横杆的铁架台、铁夹、停表、游标卡尺、刻度尺之外，还必须选用的器材，正确的一组是________。‎ A．约1 m的不可伸长的细线，半径约1 cm的小铁球 B．约0.1 m的不可伸长的细线，半径约1 cm的小铁球 C．约0.1 m的不可伸长的细线，半径约1 cm的小塑料球 D．约1 m的不可伸长的细线，半径约1 cm的小塑料球 ‎(2)测量小球直径时游标卡尺如图甲所示，读数为________cm。‎ ‎(3)某同学在处理数据的步骤中，以为纵坐标，以周期T 为横坐标，作出如图乙所示的图象，已知该图线的斜率为k＝0.500，则重力加速度为________m/s2。(结果保留三位有效数字，π＝3.14)‎ 解析：　(1)本实验应选择细、轻又不易伸长的线，长度一般在1 m左右，小球应选用直径较小、密度较大的金属球，故选A。‎ ‎(2)游标卡尺的读数为8 mm＋18×0.05 mm＝8.90 mm＝0.890 cm。‎ ‎(3)由单摆的周期公式知T＝2π ，所以＝T，可见k＝，将k＝0.500代入知g＝9.86 m/s2。‎ 答案：　(1)A　(2)0.890　(3)9.86‎ ‎7．如图甲是一个单摆振动的情形，O是它的平衡位置，B、C是摆球所能到达的最远位置。设摆球向右运动为正方向。图乙是这个单摆的振动图象。根据图象回答：‎ ‎(1)单摆振动的频率是多大？‎ ‎(2)开始时摆球在何位置？‎ ‎(3)若当地的重力加速度为10 m/s2，试求这个摆的摆长是多少？(计算结果保留两位有效数字)‎ 解析：　(1)由乙图知周期T＝0.8 s，则频率 f＝＝1.25 Hz。‎ ‎(2)由乙图知，t＝0时刻摆球在负向最大位移处，因向右为正方向，所以开始时摆球在B点。‎ ‎(3)由T＝2π 得L＝≈0.16 m。‎ 答案：　(1)1.25 Hz　(2)B点　(3)0.16 m ‎◎能力提升练 ‎8.‎ ‎(多选)甲、乙两弹簧振子的振动图象如图所示，则可知________。‎ A．两弹簧振子完全相同 B．两弹簧振子所受回复力最大值之比F甲∶F乙＝2∶1‎ C．振子甲速度为零时，振子乙速度最大 D．两振子的振动频率之比f甲∶f乙＝1∶2‎ E．振子乙速度为最大时，振子甲速度不一定为零 解析：　从图象中可以看出，两弹簧振子周期之比T甲∶T乙＝2∶1，则频率之比f甲∶f乙＝1∶2，D正确；弹簧振子周期与弹簧振子的组成有关，说明两弹簧振子不同，A错误；由于弹簧的劲度系数k不一定相同，所以两振子所受回复力(F＝－kx)的最大值之比F甲∶F乙不一定为2∶1，B错误；由简谐运动的特点可知，在振子到达平衡位置时位移为零，速度最大，在振子到达最大位移处时，速度为零，从图象中可以看出，在振子甲到达最大位移处时，振子乙恰好到达平衡位置，C正确；当振子乙到达平衡位置时，振子甲有两个可能的位置，一个是最大位移处，一个是平衡位置，E正确。‎ 答案：　CDE ‎9．(2018·温州十校联合体模拟)弹簧振子以O点为平衡位置，在B、C两点间做简谐运动，在t＝0时刻，振子从O、B间的P点以速度v向B点运动；在t＝0.2 s时，振子速度第一次变为－v；在t＝0.5 s时，振子速度第二次变为－v。‎ ‎(1)求弹簧振子振动周期T；‎ ‎(2)若B、C之间的距离为25 cm，求振子在4.0 s内通过的路程；‎ ‎(3)若B、C之间的距离为25 cm，从平衡位置开始计时，写出弹簧振子位移表达式，并画出弹簧振子的振动图象。‎ 解析：　(1)弹簧振子简谐运动示意图如图所示，由对称性可得T＝0.5×2 s＝1.0 s。‎ ‎(2)若B、C之间距离为25 cm，‎ 则振幅A＝×25 cm＝12.5 cm 振子4.0 s内通过的路程s＝×4×12.5 cm＝200 cm ‎(3)根据x＝Asin ωt，A＝12.5 cm，ω＝＝2π 得x＝12.5sin 2πt (cm)。振动图象为 答案：　(1)1.0 s　(2)200 cm　(3)x＝12.5sin 2πt (cm)　图见解析 ‎10.‎ ‎(2018·绵阳高二检测)如图所示，一个轻弹簧与一个质量为m＝0.5 kg的小球所构成的弹簧振子放在光滑金属杆上，已知该弹簧的劲度系数k＝200 N/m，O点是弹簧振子静止时的位置，今将振子向右拉10 cm到A点，此时外力对弹簧振子做功为1 J，然后由静止释放，则它在A、B之间运动，不计其他阻力，求：‎ ‎(1)振子在哪点的速度最大？最大速度为多少？‎ ‎(2)振子在A点的位移。‎ ‎(3)振子在B点的加速度。‎ 解析：　(1)由于弹簧振子在运动过程中满足机械能守恒，故在平衡位置O点的速度最大，由题意知：外力做的功转化为系统的弹性势能，该势能又全部转化成振子的动能，即W＝mv2‎ 解得：v＝＝ m/s＝2 m/s。‎ ‎(2)振子在A点的位移大小为x＝10 cm，方向由O指向A。‎ ‎(3)由于振动的振幅为10 cm，故在B点的位移大小是10 cm，即弹簧压缩10 cm，此时回复力的大小F＝kx＝200×0.1 N＝20 N，即振子所受到的合外力大小为20 N，由牛顿第二定律得：a＝＝ m/s2＝40 m/s2，方向由B指向O。‎ 答案：　(1)O点　2 m/s ‎(2)10 cm　方向由O指向A　(3)40 m/s2，方向向B指向O