高中物理人教版必修二第七章第一二节追寻守恒量—能量第二节功导学案 5页

1.追寻守恒量 2.功 问题导学 一、追寻守恒量 活动与探究 1 1．在伽 利略的斜面实验中，小球从释放点到另一侧斜面最高点的过程中，能量怎样变 化？总能量遵循什么规律？ 2．如果没有摩擦，小球将上升到原来的高度。减小倾角，小球仍能达到同一高度，但 滚得远些，如果斜面放平，小球运动情况将会怎样？ 3．在伽利略的斜面实验中，若空气阻力和摩擦力不能忽略，那么人们寻找的守恒量还 存在吗？ 迁移与应用 1 关于伽利略的斜面实验，下列描述正确的是（ ） A．伽利略斜面实验对于任意斜面都适用，都可以使小球在另一个斜面上升到同样的高 度 B．只有斜面光滑时，才有可能重复伽利略实验 C．在伽利略斜面实验中，在另一个斜面上升时，只有斜面“坡度”较缓才有可能使小 球上升到同样高度 D．设想在伽利略斜面实验中，若面光滑，并且使另一个面变成水平，则可以使小球沿 平面运动到无穷远处 1．伽利略的理想斜面实验使我们认识到不同形式能量间能发生转化并保持能量守恒， 从而引入了能量的概念。 2．能量 （1）势能：与势能大小有关的因素：物体间的相互作用力和物体间的相对位置。 （2）动能：物体的动能不但与物体的速度有关，还与物体的质量有关。 3．动能和势能在转化过程中能量 守恒。 动能和势能之间可以相互转化。若不计空气阻力和碰撞时的能量损失，动能和势能的总 量保持不变。 二、对功的正确理解 活动与探究 2 1．物体在水平恒力 F 的作用下前进的位移为 l，则力 F 做了多少功？若力与运动方向 成一角度α（如图），那么又如何表示这个力对物体所做的功呢？ 2．力可以做正功，也可以做负功，那么如何理解功的正负？ 3．摩擦力对物体一定做负功吗？试探究摩擦力做功有哪些特点？ 迁移与应用 2 如图所示，质量为 m 的物体在与水平方向成θ角的恒力 F 作用下以加速度 a 做匀加速直 线运动，已知物体和地面间的动摩擦因数为μ，物体在水平地面上运动距离 x 的过程中，力 F 做功为（ ） A．μmgx B．m(a＋μg)x 1－μtan θ C．m(a－μg)x 1＋μtan θ D． μmgx 1＋μtan θ 1．功的概念 物体在力的作用下，沿力的方向发生一段位移，则这个力对物体做了功。 2．做功的两个不可缺少的因素 （1）力；（2）物体在力的方向上发生的位移。 3．计算功的大 小的公式[来源:学#科#网] 当力的方向与运动方向成某一角度时，功的大小等于力的大小、位移的大小、力与位移 夹角的余弦这三者的乘积，W＝Flcos α。 （1）公式中的 F 是恒力，即大小、方向不变的力。 （2）公式中的α是力与位移的夹角，W＝Flcos α有两种理解：lcos α是位移 l 在 F 方向 上的分位移；Fcos α是力 F 在位移 l 方向上的分力。 （3）如果力的方向与物体运动方向一致，则 W＝Fl； 如果力的方向与物体运动方向相反，则 W＝－Fl。[来源:学科网 ZXXK] （4）计算功时，一定要明确是哪个力对物体做的功。 （5）功是标量，没有方向。功的单位是焦耳，符号是 J，由公式 W＝Fl 知，1 J＝1 N×1 m＝1 N·m。 （6）功是过程量，是力的作用效果在空间上的积累。 4．力做正功还是负功的判断方法 （1）看力 F 与位移 l 的夹角α α＜90°，力做正功；α＞90°，力做负功。 （2）看力 F 与速度 v 的夹角α α＜90°，力做正功；α＞90°，力做负功。 （3）看速率增大还是减小，若在力作用下速率增 大，此力做正功，反之做负功。 三、总功及其求法 活动与探究 3 1．如果物体受到的各个力对物体做功都不为零，那么合力对物体做功一定不为零吗？ 如果一个物体所受的合力不为零，那么合力一定对物体做功吗？ 2．若一个物体在几个力 F1、F2、F3…的共同作用下，运动的位移为 x，如何计算所有 外力对物体做的总功？ 迁移与应用 3 如图所示，利用斜面从货车上提货，每包货物的质量 m＝20 kg，斜面倾角α＝37°， 斜面的长度 l＝2 m，货物与斜面间的动摩擦因数μ＝0.2，求货物从斜面顶端滑到底端的过 程中所受合外力做的功。（取 g＝10 m/s2） 两种求 合力功的方法要依据题目特点灵活运用，如物体处于平衡状态或某一方向受力 平衡时，先求合力再求功的方法简单方便；如已知物体受力中有的不做功，有的虽做功，但 方便求得该力的功（如重力功）时，选择 W＝W1＋W2＋…＋Wn 简单方便。 四、探究变力做功的计算 活动与探究 4 如图所示，在一大小不变、方向始终沿切线方向的力 F 作用下，物体沿半径为 R 的圆 运动了一周，求力 F 做的功。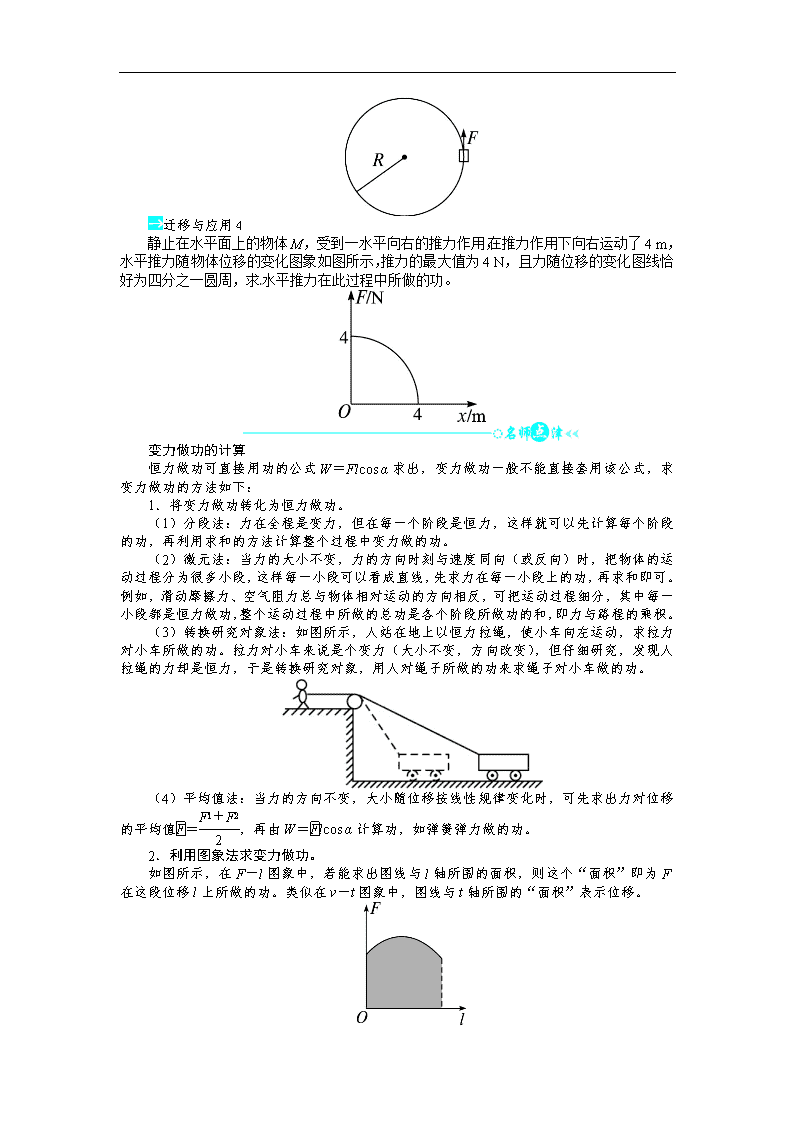 迁移与应用 4 静止在水平面上的物体 M，受到一水平向右的推力作用，在推力作用下向右运动了 4 m， 水平推力随物体位移的变化图象如图所示，推力的最大值为 4 N，且力随位移的变化图线恰 好为四分之一圆周，求 水平推力在此过程中所做的功。 变力做功的计算 恒力做功可直接用功的公式 W＝Flcos α求出，变力做功一般不能直接套用该公式，求 变力做功的方法如下： 1．将变力做功转化为恒力做功。 （1）分段法：力在全程是变力，但在每一个阶段是恒力，这样就可以先计算每个阶段 的功，再利用求和的方法计算整个过程中变力做的功。 （2）微元法：当力的大小不变，力的方向时刻与速度同向（或反向）时，把物体的运 动过程分为很多小段，这样每一小段可以看成直线，先求力在每一小段上的功，再求和即可。 例如，滑动摩擦力、空气阻力总与物体相对运动的方向相反，可把运动过程细分，其中每一 小段都是恒力做功，整个运动过程中所做的总功是各个阶段所做功的和，即力与路程的乘积。 （3）转换研究对象法：如图所示，人站在地上以恒力拉绳，使小车向左运动，求拉力 对小车所做的功。拉力对小车来说是个变力（大小不变，方向改变），但仔细研究，发现人 拉绳的力却是恒力，于是转换研究对象，用人对绳子所做的功来求绳子对小车做的功。 （4）平均值法：当力的方向不变，大小随位移按线性规律变化时，可先求出力对位移 的平均值 F ＝F1＋F2 2 ，再由 W＝ F lcos α计算功，如弹簧弹力做的功。[来源:学#科#网] 2．利用图象法求变力做功。 如图所示，在 F－l 图象中，若能求出图线与 l 轴所围的面积，则这个“面积”即为 F 在这段位移 l 上所做的功。类似在 v－t 图象中，图线与 t 轴所围的“面积”表示位移。 3．利用动能定理或能量的转化与守恒求变力做功（在后面将要学到）。 答案： 【问题导学】[来源:学科网] 活动与探究 1：1．答案：小球从释放点到斜面底部的过程中，势能逐渐转化为动能； 小球由斜面底部沿另一侧斜面上升时，动能又逐渐转化为势能。 小球运动的过程中，总能量守恒。 2．答案：小球将永远运动下去。 3．答案：在伽利略斜面实验中，若考虑空气阻力和摩擦力，小球沿另一侧上升的高度 比释放点的高度要低一些。因为小球在运动过程中，有一部分机械能转化为内能，机械能的 数值在不断减小，好像是守恒量不存在了；但是内能不断增加，机械能和内能的总量是保持 不变的，这时的守恒量应该是机械能与内能之和。因此守恒量仍然是存在的，只不过不再是 机械能守恒了。 迁移与应用 1：BD 解析：在伽利略斜面实验中，必须是阻力不计（斜面光滑）时， 小球才能在另一个斜面上上升到相同高 度，而不管另一个斜面的倾角多大。所以，在 A、B、 C 选项中 A、C 项错，B 项正确；当另一个斜面的倾角减小到接近 0°时，小球仍欲在斜面上 上升到同样高度，所以 D 项中设想是合理的。 活动与探究 2：1．答案：W＝Fl，W＝Flcos α 2．答案：功是标量，有正、负之分，但功的正、负既不表示大小，也不表示方向，只 表示是动力做功还是阻力做功。计算功时可利用公式 W＝Flcos α，其中 F 在位移 l 上应是恒 力，α是 F 与位移 l 的夹角。[来源:Z*xx*k.Com] （1）当α＝90°时，F 不做功； （2）当 0°≤α＜90°时，F 做正功，F 是动力； （3）当 90°＜α≤180°时，F 做负功，F 是阻力。 3．答案：不一定。摩擦力做功有以下特点： （1）静摩擦力可以对物体做正功、负功、不做功，原因是静摩擦力总阻碍物体间的相 对运动，而和物体的运动方向可能相同，也可能相反，或者垂直。即静摩擦力可以是动力， 也可以是阻力。 （2）滑动摩擦力和静摩擦力具有类似的做功特点，可以是动力，也可以是阻力，即滑 动摩擦力可以做正功，可以做负功，也可以不做功。 （3）摩擦力总是成对出现的，一对静摩擦力做功之和一定为零，一对滑动摩擦力做功 之和一定不为零。 迁移与应用 2：B 解析：以物体为研究对象，竖直方向有 Fsin θ＋mg＝FN，水平方向 有 Fcos θ－μFN ＝ma，联立解得 F＝ m(a＋μg) cos θ－μsin θ ，在此过程中 F 做功 W＝Fxcos θ＝ m(a＋μg)x 1－μtan θ ，故正确选项为 B。 活动与探究 3：1．答案：不为零。不一定。 2．答案：方法一：所有外力对物体做的总功等于各个力分别对物体做功的代数和：W 总＝W1＋W2＋W3＋…＝F1xcos α1＋F2xcos α2＋F3xcos α3＋… 方法二：所有外力对这个物体做的总功等于这些外力的合力对该物体做的功，即 W 总 ＝F 合 xcos α。 迁移与应用 3：答案：176 J 解 析：斜面上的货物受到重力 G、斜面支持力 FN 和摩擦力 Ff 共三个力的作用，如图所 示。 方法一：先求出各个力所做的功，再求总功。 重力 G 做的功为： W1=mglsin 37°=20×10×2×0.6 J=240 J。支持力 FN 对货物没有做功：W2=0。 摩擦力 Ff 对货物做负功为： W3=（μmgcos 37°）lcos 180°=－0.2×20×10×0.8×2 J=－64 J。 所以，合外力做的总功为 W=W1＋W 2＋W3=（240＋0－64） J=176 J。 方法二：先求货物所受的合外力，再求合外力的功。 合外力做的功为： W＝F 合 l＝（mgsin 37°－μmgcos 37°）l ＝（20×10×0.6－0.2×20×10×0.8）×2 J＝176 J。 活动与探究 4：答案：2πR·F 解析：力 F 的方向时刻在改变，且沿切线方向，把整个圆分成无数段，每一小段圆弧 可视为与力 F 方向一致，则ΔW＝F·Δl，当沿圆运动一圈时，W＝ΔW1＋ΔW2＋…＝FΔl1＋FΔl2 ＋…＝F·（Δl1＋Δl2＋…）＝2πR·F。 迁移与应用 4：答案：12.56 J 解析：推力随位移逐渐减小，不属于恒力做功，不能直接用 W＝Flcos α来求。可根据 面积求推力做功。 W＝πR2 4 ＝π×16 4 J＝12.56 J。