高中物理人教版必修二第五章第六节向心力导学案 4页

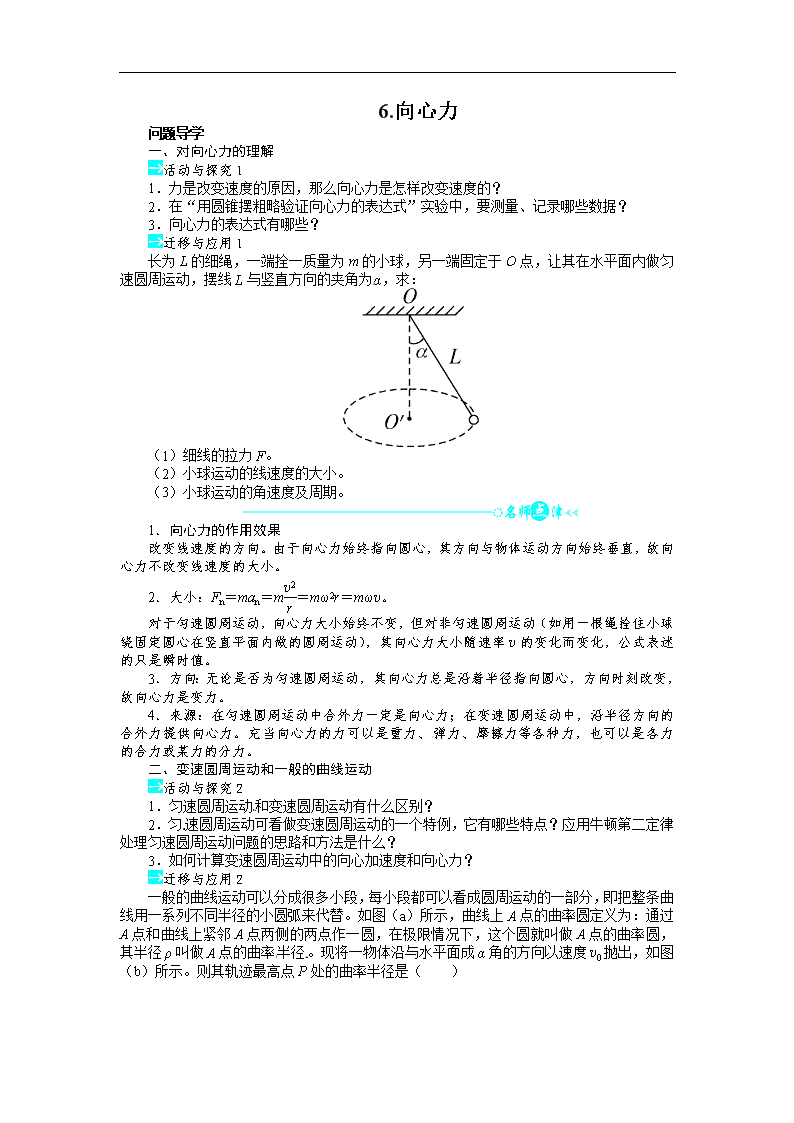
6.向心力 问题导学 一、对向心力的理解 活动与探究 1 1．力是改变速度的原因，那么向心力是怎样改变速度的？ 2．在“用圆锥摆粗略验证向心力的表达式”实验中，要测量、记录哪些数据？ 3．向心力的表达式有哪些？ 迁移与应用 1 长为 L 的细绳，一端拴一质量为 m 的小球，另一端固定于 O 点，让其在水平面内做匀 速圆周运动，摆线 L 与竖直方向的夹角为α，求： （1）细线的拉力 F。 （2）小球运动的线速度的大小。 （3）小球运动的角速度及周期。 1．向心力的作用效果 改变线速度的方向。由于向心力始终指向圆心，其方向与物体运动方向始终垂直，故向 心力不改变线速度的大小。 2．大小：Fn＝man＝mv2 r ＝mω2r＝mωv。 对于匀速圆周运动，向心力大小始终不变，但对非匀速圆周运动（如用一根绳拴住小球 绕固定圆心在竖直平面内做的圆周运动），其向心力大小随速率 v 的变化而变化，公式表述 的只是瞬时值。 3．方向：无论是否为匀速圆周运动，其向心力总是沿着半径指向圆心，方向时刻改变， 故向心力是变力。[来源:Zxxk.Com] 4．来源：在匀速圆周运动中合外力一定是向心力；在变速圆周运动中，沿半径方向的 合外力提供向心力。充当向心力的力可以是重力、弹力、摩擦力等各种力，也可以是各力 的合力或某力的分力。 二、变速圆周运动和一般的曲线运动 活动与探究 2 1．匀速圆周运动 和变速圆周运动有什么区别？ 2．匀 速圆周运动可看做变速圆周运动的一个特例，它有哪些特点？应用牛顿第二定律 处理匀速圆周运动问题的思路和方法是什么？ 3．如何计算变速圆周运动中的向心加速度和向心力？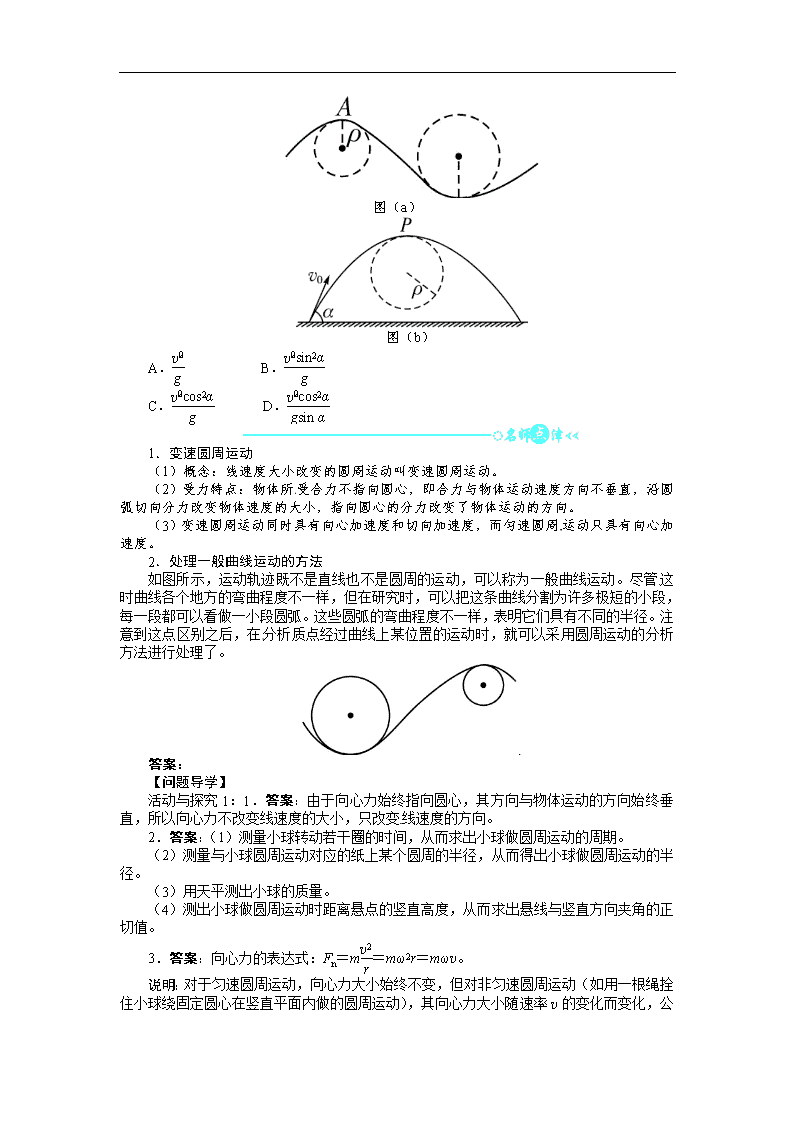[来源:学科网 ZXXK] 迁移与应用 2 一般的曲线运动可以分成很多小段，每小段都可以看成圆周运动的一部分，即把整条曲 线用一系列不同半径的小圆弧来代替。如图（a）所示，曲线上 A 点的曲率圆定义为：通过 A 点和曲线上紧邻 A 点两侧的两点作一圆，在极限情况下，这个圆就叫做 A 点的曲率圆， 其半径ρ叫做 A 点的曲率半径 。现将一物体沿与水平面成α角的方向以速度 v0 抛出，如图（b） 所示。则其轨迹最高点 P 处的曲率半径是（ ） 图（a）[来源:学|科|网 Z|X|X|K] 图（b） A．v20 g B．v20sin2α g C．v20cos2α g D．v20cos2α gsin α 1．变速圆周运动 （1）概念：线速度大小改变的圆周运动叫变速圆周运动。 （2）受力特点：物体所受合力不指向圆心，即合力与物体运动速度方向不垂直，沿圆 弧切向分力改变物体速度的大小，指向圆心的分力改变了物体运动的方向。 （3）变速圆周运动同时具有向心加速度和切向加速度，而匀速圆周 运动只具有向心加 速度。 2．处理一般曲线运动的方法 如图所示，运动轨迹既不是直线也不是圆周的运动，可以称为一般曲线运动。尽管这 时曲线各个地方的弯曲程度不一样，但在研究时，可以把这条曲线分割为许多极短的小段， 每一段都可以看做一小段圆弧。这些圆弧的弯曲程度不一样，表明它们具有不同的半径。注 意到这点区别之后，在分析质点经过曲线上某位置的运动时，就可以采用圆周运动的分析 方法进行处理了。 答案： 【问题导学】 活动与探究 1：1．答案：由于向心力始终指向圆心，其方向与物体运动的方向始终垂 直，所以向心力不改变线速度的大小，只改变线速度的方向。 2．答案：（1）测量小球转动若干圈的时间，从而求出小球做圆周运动的周期。 （2）测量与小球圆周运动对应的纸上某个圆周的半径，从而得出小球做圆周运动的半 径。 （3）用天平测出小球的质量。[来源:学科网 ZXXK] （4）测出小球做圆周运动时距离悬点的竖直高度，从而求出悬线与竖直方向夹角的正 切值。 3．答案：向心力的表达式：Fn＝mv2 r ＝mω2r＝mωv。 说明：对于匀速圆周运动，向心力大小始终不变，但对非匀速圆周运动（如用一根绳拴 住小球绕固定圆心在竖直平面内做的圆周运动），其向心力大小随速率 v 的变化而变化，公 式表述的只是瞬时值。 迁移与应用 1：答案：（1） mg cos α （2） gLtan α·sin α （3） g Lcos α 2π Lcos α g 解析：做匀速圆周运动的小球受力如图所示，小球受重力 mg 和细线的拉力 F 的作用。 （1）因为小球在水平面内做匀速圆周运动，所以小球受到的合力沿水平方向指向圆心 O′。由平行四边形定则得小球受到的合力大小为 mgtanα，细线对小球的拉力大小为 cos mgF  。 （2）由牛顿第二定律得 mgtan α= 2mv r 由几何关系得 r＝Lsin α 所以，小球做匀速圆周运动的线速度的大小为 tan sinv gL    。 （3）小球运动的角速度ω＝v r ＝ gLtan α·sin α Lsin α ＝ g Lcos α 小球运动的周期 T＝2π ω ＝2π Lcos α g 。 活动与探究 2：1．答案：由做曲线运动的条件可知，变速圆周运动中物体所受的合力 与速度方向一定不垂直，当速率增大时，物体受到的合力与瞬时速度之间的夹角是锐角；当 速率减小时，物体受到的合力与速度之间的夹角是钝角。 例如：用一细线系一小球在竖直平面内做变速圆周运动，在向下加速运动过程的某一位 置 A 和向上减速运动过程的某一位置 B，小球的受力情况如图所示。 比较可知，匀速圆周运动和变速圆周运动受力情况的不同是：匀速圆周运动中，合力全 部用来提供向心力，合力指向圆心；变速圆周运动中，合力沿着半径方向的分量提供向心力， 合力通常不指向圆心。 2．答案：（1）匀速圆周运动中的线速度大小、向心加速度大小及向心力的大小都是恒 定不变的，改变的只是它们的方向。因而匀速圆周运动中的线速度 v、向心加速度 an 及向心 力 Fn 都是变量。而匀速圆周运动中的角速度、周期和频率都是恒定不变的。 匀速圆周运动中只存在向心加速度，不存在切向加速度，物体所受外力的合力就是物体 做匀速圆周运动的向心力。[来源:Z#xx#k.Com] （2）解题思路：物体做匀速圆周运动需要的向心力是由物体所受外力的合力提供，即 F 合＝mv2 r ＝mrω2＝mvω＝mr4π2 T2 ＝man。 解题步骤：①明确研究对象，对研究对象进行受力分析，画出受力示意图。 ②将物体所受外力通过力的正交分解将其分解在两条直线上，其中一个方向上的分力沿 半径方向。 ③列方程：沿半径方向满足 F 合 1＝mrω2＝mv2 r ＝4π2mr T2 ，另一方向 F 合 2＝0。 ④解方程求出结果。 3．答案：变速圆周运动的速度方向和大小都是变化的，因此，做变速圆周运动的物体， 既存在改变速度方向的向心加速度，又存在改变速度大小的切向加速度，其实际的加速度为 向心加速度和切向加速度的合加速度。合加速度的方向是不指向圆心的，因而物体所受合 外力的方向也是不指向圆心的。对变速圆周运动，计算向心加速度大小的公式仍是适用的， 只不过应注意计算某时刻的向心加速度时，应取与该时刻对应的．．．瞬时速度或瞬时角速度。继 而根据牛顿第二定律求出的向心力，也不再是物体 所受的合外力，而是该合外力沿半径方 向的分力。 迁移与应用 2：C 解析：物体被抛出后做斜上抛运动，在其轨迹最高点 P 处时，竖直 方向速度为 0，水平方向 速度 v＝v0cos α，在最高点 P 处的曲率半径是ρ，此时，可以认为 是圆周运动的一部分，由重力提供其向心力，即 mg＝mv2 ρ ，解得ρ＝v20cos2α g ，C 正确。