2018届二轮复习　功能关系在力学中的应用课件（共43张）（全国通用） 43页

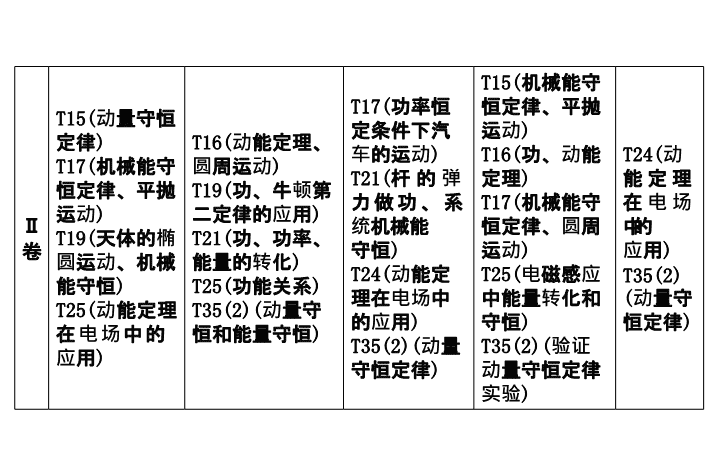
专题四　能量与动量 定位 五年考情分析 2017年 2016年 2015年 2014年 2013年 Ⅰ 卷 T14(动量守恒 定律) T24(机械能、 功能关系) T20(电场中 的能量转化) T25(动能定 理、平抛运 动、多过程 中的能量转 化和守恒) T35(2)(动量 定理) T17(功、动 能 定 理 的 应用) T21(机械能 守恒定律的 条件) T35(2)(动量 守恒定律) T25(动能定 理、能量守 恒在复合场 中的应用) T35(2)(动量 守恒定律) T16(动能定 理在电场中 的应用) T21(功率、 v-t图像) T35(2)(动 量 守 恒 定 律) Ⅱ 卷 T15(动量守恒 定律) T17(机械能守 恒定律、平抛 运动) T19(天体的椭 圆运动、机械 能守恒) T25(动能定理 在 电 场 中 的 应用) T16(动能定理、 圆周运动) T19(功、牛顿第 二定律的应用) T21(功、功率、 能量的转化) T25(功能关系) T35(2)(动量守 恒和能量守恒) T17(功率恒 定条件下汽 车的运动) T21(杆的弹 力 做 功 、 系 统 机 械 能 守恒) T24(动能定 理在电场中 的应用) T35(2)(动量 守恒定律) T15(机械能守 恒定律、平抛 运动) T16(功、动能 定理) T17(机械能守 恒定律、圆周 运动) T25(电磁感应 中能量转化和 守恒) T35(2)(验证 动量守恒定律 实验) T 2 4 ( 动 能 定 理 在 电 场 中 的 应用) T35(2) (动量守 恒定律) Ⅲ卷 T 1 6 ( 功 能 关系) T20(动量、 动量定理) T20(动能定理、圆周运动) T24(动能定理、能量守恒 定律的应用) T35(2)(动量守恒和能量 守恒) 专题定位 本专题解决的是机械能守恒、功能关系,动量和动量守恒.高考对本专题的 考查频率极高,选择题与计算题都可能出现,难度多为中低档.主要题型有: 功能关系与图像问题的结合,能量守恒、牛顿运动定律、曲线运动及电磁 学的综合,以碰撞为模型与弹簧结合的问题等.整体法与隔离法、图像法、 转换法、类比思想和守恒思想是用到的主要思想方法. 应考建议 熟练运用动能定理解决综合问题,注意和图像有关的题型,提高运用能量观 点解决电、磁场中运动问题的能力,抓住动力学、能量和动量三条主线. 第1讲　功能关系在力学中的应用 整 合 突 破 实 战 整合 网络要点重温 【网络构建】 【要点重温】 1.功 (1)恒力做功:W= . (2)变力做功:①用 求解;②用F-x图线与x轴所围“ ”求 解. 2.功率 Flcos α 动能定理 面积 (2)瞬时功率:P=Fvcos α. (3)机车启动两类模型中的关键方程:P=F·v,F-f=ma. 4.系统机械能守恒的三种表达式 E1=E2 突破 热点考向聚焦 热点考向一　力学中几个重要功能关系的应用 【核心提炼】 1.力学中几种功能关系. (1)合外力做功与动能的关系:W合=ΔEk. (2)重力做功与重力势能的关系:WG=-ΔEp. (3)弹力做功与弹性势能的关系:W弹=-ΔEp. (4)除重力以外其他力做功与机械能的关系:W其他=ΔE机. (5)滑动摩擦力做功与内能的关系:fl相对=ΔE内. 2.分清是什么力做功,并且分析该力做正功还是做负功;根据功能之间的对应关 系,判定能的转化形式,确定能量之间的转化情况. 【典例1】 (2017·辽宁大连模拟)如图所示,质量为m的物体(可视为质点)以某 一速度从A点冲上倾角为30°的斜面,其运动的加速度为 g,此物体在斜面上 上升的最大高度为h,则在这个过程中物体(　 　) A.重力势能增加了mgh B.重力势能增加了 mgh C.动能损失了mgh D.机械能损失了 mgh A 3 4 3 43 4 【预测练习1】 (多选)如图所示,质量为m的小球套在倾斜放置的固定光滑杆 上,一根轻质弹簧的一端悬挂于O点,另一端与小球相连,弹簧与杆在同一竖直 平面内,将小球沿杆拉到弹簧水平位置由静止释放,小球沿杆下滑,当弹簧位于 竖直位置时,小球速度恰好为零,此时小球下降的竖直高度为h,若全过程中弹 簧始终处于伸长状态且处于弹性限度范围内,下列说法正确的是(　 　) A.弹簧与杆垂直时,小球速度最大 B.弹簧与杆垂直时,小球的动能与重力势能之和最大 C.小球下滑至最低点的过程中,弹簧的弹性势能增加量小于mgh D.小球下滑至最低点的过程中,弹簧的弹性势能增加量等于mgh BD 解析:光滑杆没有摩擦力做功,杆的弹力和运动方向垂直,也不做功,那么整 个过程只有弹簧弹力和小球重力做功,二者组成的系统机械能守恒,分析小 球的受力,在沿杆方向一个是自身重力分力,另外一个是弹力沿杆方向的分 力,当弹簧与杆垂直时,沿杆方向没有弹簧的分力,只有重力沿杆向下的分 力,说明小球在沿杆向下加速,所以速度不是最大,选项A错误;由于全过程 弹簧始终处于伸长状态,那么弹簧与杆垂直时弹簧伸长量最小,弹性势能最 小,根据小球和弹簧组成的系统机械能守恒,此时小球机械能最大,即动能 和重力势能之和最大,选项B正确;从初位置到末位置,小球速度都是零,故 动能不变,重力势能减小mgh,根据系统机械能守恒,弹簧弹性势能增加mgh, 选项D正确,C错误. 热点考向二　动力学规律和动能定理的综合应用 【核心提炼】 1.对单个物体的动能增量的判断宜采用动能定理,而对物体系统动能增量的大 小判断则应考虑应用能量守恒定律. 2.动能定理表达式是一个标量式,在某个方向上应用动能定理是没有依据的. 3.物体在某个运动过程中包含有几个运动性质不同的小过程(如加速、减速的 过程),此时可以分段考虑,也可以对全过程考虑,但若能对整个过程利用动能定 理列式则可使问题简化. 【典例2】 (2017·全国Ⅱ卷,24)为提高冰球运动员的加速能力,教练员在冰面 上与起跑线距离s0和s1(s1