匀速圆周运动研究·典型例题精析 7页

匀速圆周运动研究·典型例题精析 ‎[例题1]　 如图5－26所示，O1皮带传动装置的主动轮的轴心，轮的半径为r1；O2为从动轮的轴心，轮的半径为r2；r3为与从动轮固定在一起的大轮的半径．已知r2＝1.5r1，r3=2r1．A、B、C分别是三个轮边缘上的点，那么质点A、B、C的线速度之比是_________ ，角速度之比是_________ ，向心加速度之比是__________ ，周期之比是_________．‎ ‎[思路点拨] 　本题涉及了匀速圆周运动的所有基本公式：v=ωR，‎ 之间关系的两种不同形式，并应正确理解其含义．‎ ‎[解题过程]　 由于A、B轮由不打滑的皮带相连，故vA=vB．‎ 所以ωB=ωC．‎ 所以有　 ωA∶ωB∶ωC=3∶2∶2， vA∶vB∶vC＝3∶3∶4．‎ 故　 aA∶aB∶aC=9∶6∶8．‎ ‎[小结] 　物体做匀速圆周运动时，线速度、角速度、向心加速度、向心力和轨道半径间有一定牵连关系．“认为线速度一定与半径成正比”是不对的，其实只有在角速度不变的情况下才成立．同样泛泛地讲：向心加速度与半径成正比还是成反比，也是不对的，必须讲清其物理条件是角速度不变还是线速度不变．对此初学者务必注意．‎ ‎[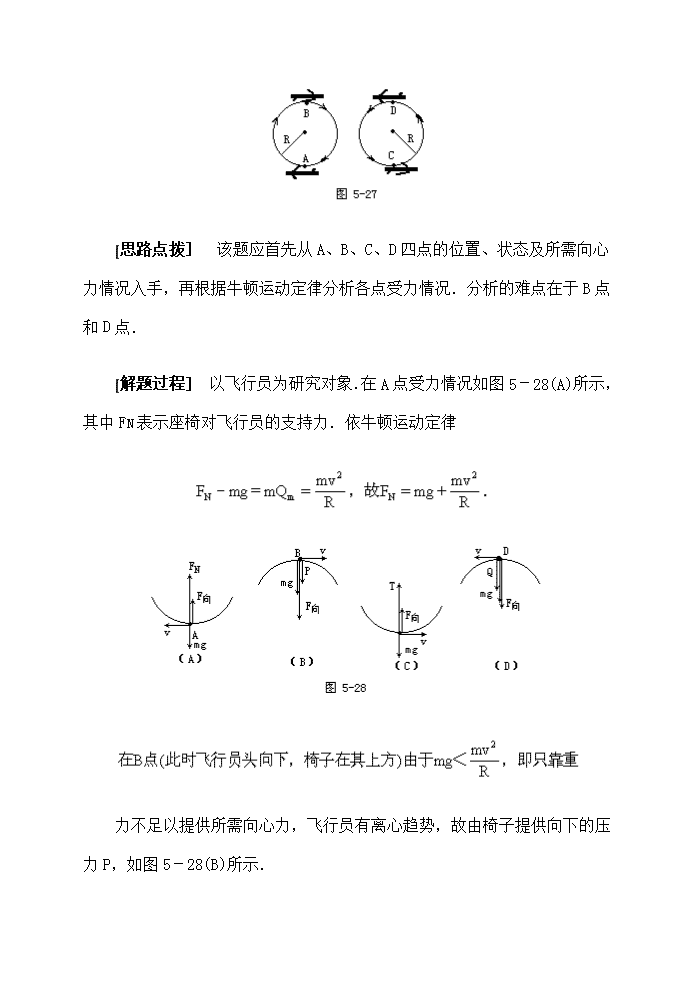例题2]　 如图5－27所示，一飞机在竖直平面内做匀速率特技飞 C、D四个位置受力情况．‎ ‎[思路点拨]　 该题应首先从A、B、C、D四点的位置、状态及所需向心力情况入手，再根据牛顿运动定律分析各点受力情况．分析的难点在于B点和D点．‎ ‎[解题过程]　 以飞行员为研究对象．在A点受力情况如图5－28(A)所示，其中FN表示座椅对飞行员的支持力．依牛顿运动定律 力不足以提供所需向心力，飞行员有离心趋势，故由椅子提供向下的压力P，如图5－28(B)所示．‎ 在C点(此时飞行员头向下，椅子在其上方)受力情况如图5－28(C)所示，其中T表示安全带对飞行员向上拉力．并有 在D点，情况与B点相近，飞行员重力不足以提供所需向心力，有离心趋势．故将由安全带提供向下的压力Q，如图5－28(D)所示．‎ ‎[小结]　 (1)物体的匀速圆周运动状态不是平衡状态．它所需要的向心力应恰好由物体所受的合外力来提供，由受力分析入手，正确使用动力学求解，是分析这类问题的主要方法．‎ ‎(2)“离心”与“向心”现象的出现，是由于提供的合外力与某状态下所需的向心力之间出现矛盾，当“供”大于“需”时，将出现“向心”．例 ‎“供”小于“需”时，物体将远离圆心被甩出，例如甩干机就是这个道理．‎ ‎[例题3]　 如图5－29所示的水平转盘可绕竖直轴OO′旋转，盘上水平杆上穿着两个质量相等的小球A和B．现将A和B分别置于距轴r和2r处，并用不可伸长的轻绳相连．已知两球与杆之间的最大静摩擦力都是fm．试分析转速ω从零逐渐增大，两球对轴保持相对静止过程中，A、B受力情况如何变化？‎ ‎[思路点拨]　 当转动角速度ω增大到某值时，A和B将发生离心现象，向B一侧甩出，此时A所受摩擦力应沿杆指向外侧．而刚开始转动时，A所受摩擦力应指向圆心(轴)，而且绳上没有张力．显然整个过程中A、B受力发生了明显变化，而且这种变化又与几个特定角速度值有关．找出这几个特定角速度是分析的关键．‎ ‎[解题过程]　 由于ω从零开始逐渐增大，当ω较小时，A和B只靠自身静摩擦力提供向心力．‎ A球：mω2r = fA；B球：mω22r = fB．‎ 随ω增大，静摩擦力不断增大，直至ω＝ω1时将有fB=fm．即 力T将出现．‎ A球：mω2r = fA＋T；B球：mω22r = fm＋T．‎ 由B球可知：当角速度由ω增至ω′时，绳上张力将增加ΔT，ΔT=m·2r(ω′2－ω2)．对于A球应有 m·r(ω′2－ω2)=ΔfA＋ΔT=ΔfA＋m·2r(ω′2－ω2)．‎ 可见ΔfA＜0，即随ω的增大，A球所受摩擦力将不断减小，直至 当角速度从ω2继续增加时，A球所受的摩擦力方向将沿杆指向外侧，并随ω的增大而增大，直至fA=fm为止．设此时角速度为ω3，并有 从ω3若角速度继续增加，A和B将一起向B一侧甩出．‎ ‎[小结]　 (1)本题很好地反映了在匀速圆周运动的角速度ω动态变化的过程中，由于所需向心力的变化对所提供的摩擦力及绳上拉力的制约作用，并最终达到供与需之间的和谐．‎ ‎(2)教学实践表明：同学们基本都能正确指出，“AB系统将最终向B一侧甩出”这一物理现象．但是对于中间动态变化过程是怎样的？为什么是这样的？却很少有人讲清楚．对于一个题目物理过程的挖掘，要深刻、要细致，只有这样才能使自己跳出题海．‎