【物理】2020届一轮复习人教版库仑定律电场力的性质课时作业 8页

‎2020届一轮复习人教版 库仑定律电场力的性质 课时作业 ‎1．真空中有两个静止的点电荷，它们之间静电力的大小为F.若保持这两个点电荷之间的距离不变，而将它们的电荷量都变为原来的，则它们之间静电力的大小变为(　A　)‎ A.　　　　B.　　　　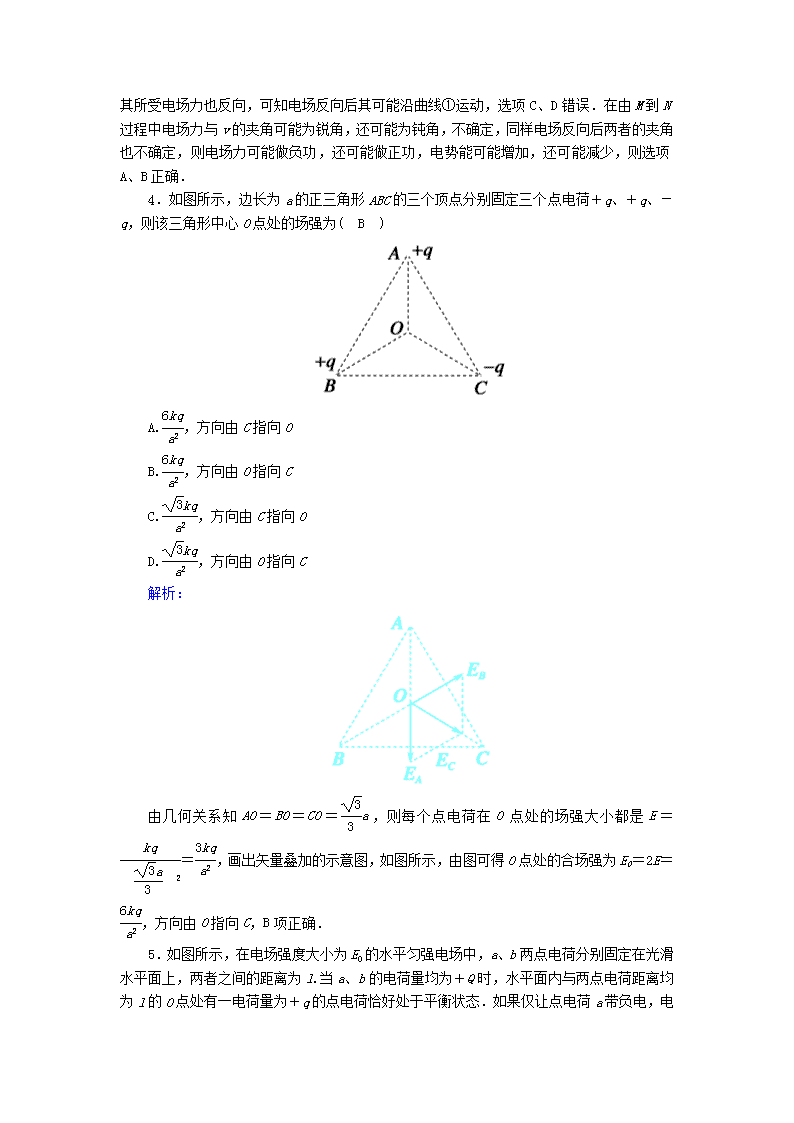C．‎4F　　　　D．‎‎16F 解析：由库仑定律F＝可知：若保持这两个点电荷之间的距离不变，而将它们的电荷量都变为原来的，则它们之间静电力的大小变为原来的，即，A正确．‎ ‎2．两个负点电荷分别固定在A、B两处，如图所示．A处电荷带电荷量为Q1，B处电荷带电荷量为Q2，且Q2＝6Q1.另取一个可以自由移动的点电荷Q3，放在A、B所在的直线上，欲使Q3受力平衡，则(　C　)‎ A．Q3为负电荷，且放于A左侧 B．Q3为负电荷，且放于B右侧 C．Q3为正电荷，且放于A、B之间 D．Q3为正电荷，且放于B右侧 解析：根据共点力平衡条件可知，Q3受力平衡时的位置应位于A、B之间，且靠近A处，带正、负电荷均可以，则C正确．‎ ‎3．(多选)如图所示，带电粒子在匀强电场中以初速度v0沿曲线从M运动到N(不计粒子的重力)，这时突然使电场方向反向而大小不变．在新的电场中，带电粒子以后的运动情况(图中三条虚线在N点都与MN相切)，下列说法正确的是(　AB　)‎ A．可能沿曲线①运动且电势能减小 B．可能沿曲线①运动且电势能增大 C．可能沿直线②运动且电势能不变 D．可能沿曲线③运动且电势能增大 解析：粒子在由M到N的过程中，所受到的电场力指向轨迹弯曲的内侧，则电场反向后，其所受电场力也反向，可知电场反向后其可能沿曲线①运动，选项C、D错误．在由M到N 过程中电场力与v的夹角可能为锐角，还可能为钝角，不确定，同样电场反向后两者的夹角也不确定，则电场力可能做负功，还可能做正功，电势能可能增加，还可能减少，则选项A、B正确．‎ ‎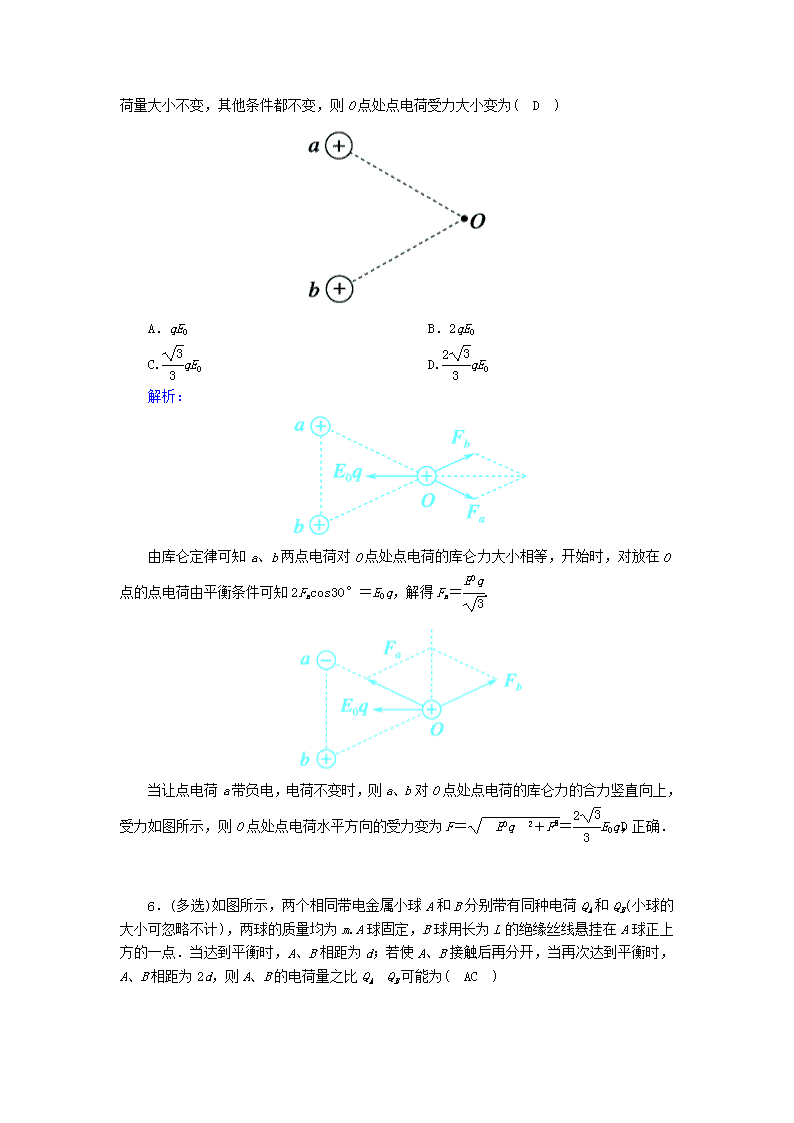4．如图所示，边长为a的正三角形ABC的三个顶点分别固定三个点电荷＋q、＋q、－q，则该三角形中心O点处的场强为(　B　)‎ A.，方向由C指向O B.，方向由O指向C C.，方向由C指向O D.，方向由O指向C 解析：‎ 由几何关系知AO＝BO＝CO＝a，则每个点电荷在O点处的场强大小都是E＝＝，画出矢量叠加的示意图，如图所示，由图可得O点处的合场强为EO＝2E＝，方向由O指向C，B项正确．‎ ‎5．如图所示，在电场强度大小为E0的水平匀强电场中，a、b两点电荷分别固定在光滑水平面上，两者之间的距离为l.当a、b的电荷量均为＋Q时，水平面内与两点电荷距离均为l的O点处有一电荷量为＋q的点电荷恰好处于平衡状态．如果仅让点电荷a带负电，电荷量大小不变，其他条件都不变，则O点处点电荷受力大小变为(　D　)‎ A．qE0 B．2qE0‎ C.qE0 D.qE0‎ 解析：‎ 由库仑定律可知a、b两点电荷对O点处点电荷的库仑力大小相等，开始时，对放在O点的点电荷由平衡条件可知2Facos30°＝E0q，解得Fa＝.‎ 当让点电荷a带负电，电荷不变时，则a、b对O点处点电荷的库仑力的合力竖直向上，受力如图所示，则O点处点电荷水平方向的受力变为F＝＝E0q，D正确．‎ ‎6．(多选)如图所示，两个相同带电金属小球A和B分别带有同种电荷QA和QB(小球的大小可忽略不计)，两球的质量均为m.A球固定，B球用长为L的绝缘丝线悬挂在A球正上方的一点．当达到平衡时，A、B相距为d；若使A、B接触后再分开，当再次达到平衡时，A、B相距为2d，则A、B的电荷量之比QAQB可能为(　AC　)‎ A．(15＋4)1 B．41‎ C．(15－4)1 D．14‎ 解析：‎ 对B进行受力分析可知，受重力mg、库仑力F、拉力T作用，如图所示．设A离悬挂点的距离为h，由平衡条件可知库仑力F与拉力T的合力与重力平衡，即F合＝mg，由力的三角形与几何三角形相似得＝，解得F＝mg.由题可知h不变，mg不变，当A、B间距离变为2d时，则库仑力F′＝mg.又F＝k，因A、B带同种电荷，故A、B接触后电荷量平分，且都为，则F′＝k，代入F′＝‎2F，得k＝2×k，解得QAQB＝(15±4)1，A、C正确．‎ ‎7．如图装置可用来研究电荷间的相互作用，带电球A固定于绝缘支架上．质量为m、电荷量为q的带电小球B用长为L的绝缘轻绳悬挂，小球B处于静止状态时绳与竖直方向的夹角为θ(此时小球B所受的电场力水平向右，小球B体积很小，重力加速度用g表示)．求：‎ ‎(1)小球B所受电场力的大小F；‎ ‎(2)带电球A在小球B处产生的电场强度的大小E；‎ ‎(3)由于漏电，A的电荷量逐渐减小至零，与此同时小球B缓慢回到最低点，求此过程中电场力对B做的功W(不计其他能量损失)．‎ 解析：(1)小球B在重力、电场力和拉力作用下处于静止状态，根据平衡条件得电场力大小F＝mgtanθ.‎ ‎(2)由场强的定义可知E＝＝.‎ ‎(3)对小球B缓慢回到最低点的过程应用动能定理有W＋mgL(1－cosθ)＝0，可得此过程中电场力做的功W＝－mgL(1－cosθ)．‎ 答案：(1)mgtanθ　(2)　(3)－mgL(1－cosθ)‎ ‎8．如图所示，实线表示电场线，虚线表示只受电场力作用的带电粒子的运动轨迹，粒子先经过M点，再经过N点．下列说法中正确的有(　C　)‎ A．粒子带负电 B．粒子在M点的动能大于在N点的动能 C．粒子在M点的电势能大于在N点的电势能 D．粒子在M点受到的电场力大于在N点受到的电场力 解析：由粒子的运动轨迹和电场线的方向可判断粒子带正电，A错；粒子从M向N运动，相当于顺着电场线方向运动，粒子又是带正电，则电场力做正功，电势能减小，可得EpM>EpN，再由动能定理知，EkMFM，D错．‎ ‎9．(2019·厦门模拟)(多选)如图所示，倾角为θ的斜面体c置于水平地面上，小物块b置于斜面上，通过绝缘细绳跨过光滑的定滑轮与带正电小球M连接，连接b的一段细绳与斜面平行，带负电的小球N用绝缘细线悬挂于P点．设两带电小球在缓慢漏电的过程中，两球心始终处于同一水平面，并且b、c都处于静止状态，下列说法中正确的是(　BC　)‎ A．b对c的摩擦力一定减小 B．地面对c的支持力一定变大 C．地面对c的摩擦力方向一定向左 D．地面对c的摩擦力一定变大 解析：当两带电小球在缓慢漏电的过程中，依据库仑定律，两电荷受到的库仑力在减小，由平衡条件可知绳子对M的拉力减小，因此绳子对b的拉力减小，若b相对c有上滑的趋势，那么其受到的摩擦力会减小，若b相对c有下滑的趋势，那么其受到的摩擦力会增大，故A错误；对b、c整体，由于绳子对整体的拉力减小，由平衡条件得地面对整体的支持力增大，而地面对整体向左的静摩擦力会减小，故B、C正确，D错误．‎ ‎10．(2019·北京石景山一模)如图所示，直径为L的光滑绝缘半圆环固定在竖直面内，电荷量为q1、q2的两个正点电荷分别置于半圆环的两个端点A、B处，半圆环上穿着一带正电的小球(可视为点电荷)，小球静止时位于P点，PA与AB间的夹角为α.若不计小球的重力，下列关系式中正确的是(　A　)‎ A．tan3α＝ B．tan2α＝ C．tan3α＝ D．tan2α＝ 解析：‎ 对小球进行受力分析，如图所示．根据库仑定律有F1＝k，r1＝Lcosα①，F2＝k，r2＝Lsinα②，根据平衡条件有F1sinα＝F2cosα③，联立①②③解得tan3α＝，故B、C、D错误，A正确．‎ ‎11．(2019·广西柳州模拟)如图所示，A、B、C三个小球(可视为质点)的质量分别为m、‎2m、‎3m，B小球带负电，电荷量为q，A、C两小球不带电(不考虑小球间的静电感应)，不可伸长的绝缘细线将三个小球连接起来悬挂在O点，三个小球均处于竖直向上的匀强电场中，电场强度大小为E，以下说法正确的是(　A　)‎ A．静止时，A、B两小球间细线的拉力为5mg＋qE B．静止时，A、B两小球间细线的拉力为5mg－qE C．剪断O点与A小球间细线的瞬间，A、B两小球间细线的拉力为qE D．剪断O点与A小球间细线的瞬间，A、B两小球间细线的拉力为qE 解析：静止时，对BC两球进行受力分析，则有：FT＝2mg＋3mg＋qE＝5mg＋qE，A正确，B错误；B球带负电，相当于在上述状态下给B球瞬间施加一个竖直向下的电场力qE，qE对A、B球整体产生一个竖直向下的加速度，此时A、B球的加速度为aA＝g＋>g，C球以加速度g保持自由下落，以A球为研究对象可得A、B球间细线的拉力为FT，由牛顿第二定律，则有FT＋mg＝maA，解得FT＝qE，C、D错误．‎ ‎12．如图所示，水平地面上方分布着水平向右的匀强电场，有圆弧形的绝缘硬质管竖直固定在匀强电场中，圆心与管口在同一水平线上，管的半径为R，下端管口切线水平，离水平地面的距离为h，有一质量为m的带电荷量＋q的小球从管的上端口A由静止释放，小球与管间摩擦不计，小球从下端管口飞出时，管壁对小球的作用力为4mg，g取‎10 m/s2.求：‎ ‎(1)小球运动到管口B时的速度大小．‎ ‎(2)匀强电场的场强．‎ ‎(3)若R＝‎0.3 m，h＝‎5.0 m，小球落地时的速度大小．‎ 解析：(1)小球从下端管口飞出时，由牛顿第二定律得：‎ FN－mg＝m　解得：vB＝ ‎(2)小球从A运动到管口B的过程中，由动能定理得：‎ mgR＋qER＝mv　解得：E＝ ‎(3)小球离开管口B后，水平方向做匀加速运动，竖直方向做自由落体运动，则有：‎ 竖直方向：h＝gt2‎ 解得：t＝1 s　vy＝gt＝‎10 m/s 水平方向：qE＝ma　vx＝vB＋at　解得：vx＝‎8 m/s 故：v＝＝‎2 m/s 答案：(1)　(2)　(3)‎2 m/s