【物理】2020届一轮复习人教版实验：验证力的平行四边形定则课时作业 8页

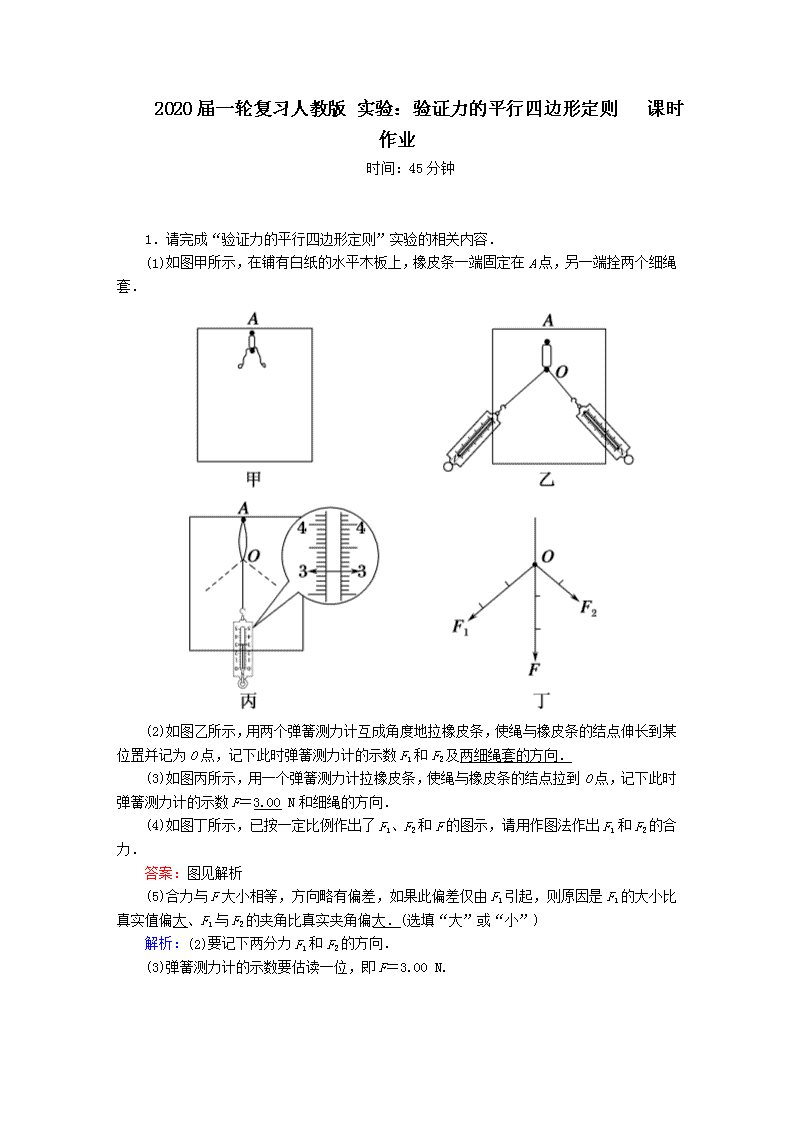
‎2020届一轮复习人教版 实验：验证力的平行四边形定则 课时作业 时间：45分钟 ‎1．请完成“验证力的平行四边形定则”实验的相关内容．‎ ‎(1)如图甲所示，在铺有白纸的水平木板上，橡皮条一端固定在A点，另一端拴两个细绳套．‎ ‎(2)如图乙所示，用两个弹簧测力计互成角度地拉橡皮条，使绳与橡皮条的结点伸长到某位置并记为O点，记下此时弹簧测力计的示数F1和F2及两细绳套的方向．‎ ‎(3)如图丙所示，用一个弹簧测力计拉橡皮条，使绳与橡皮条的结点拉到O点，记下此时弹簧测力计的示数F＝3.00 N和细绳的方向．‎ ‎(4)如图丁所示，已按一定比例作出了F1、F2和F的图示，请用作图法作出F1和F2的合力．‎ 答案：图见解析 ‎(5)合力与F大小相等，方向略有偏差，如果此偏差仅由F1引起，则原因是F1的大小比真实值偏大、F1与F2的夹角比真实夹角偏大．(选填“大”或“小”)‎ 解析：(2)要记下两分力F1和F2的方向．‎ ‎(3)弹簧测力计的示数要估读一位，即F＝3.00 N.‎ ‎(4)由力的图示作出F1和F2的合力F′，如图．‎ ‎(5)由图所示，将F1减小或减小F1与F的夹角，合力F′与F更接近重合，则原因是F1的大小比真实值偏大、F1与F2的夹角比真实夹角偏大．‎ ‎2．某同学找到一条遵循胡克定律的橡皮筋来验证力的平行四边形定则，设计了如下实验：‎ ‎(1)将橡皮筋的两端分别与两条细线相连，测出橡皮筋的原长；‎ ‎(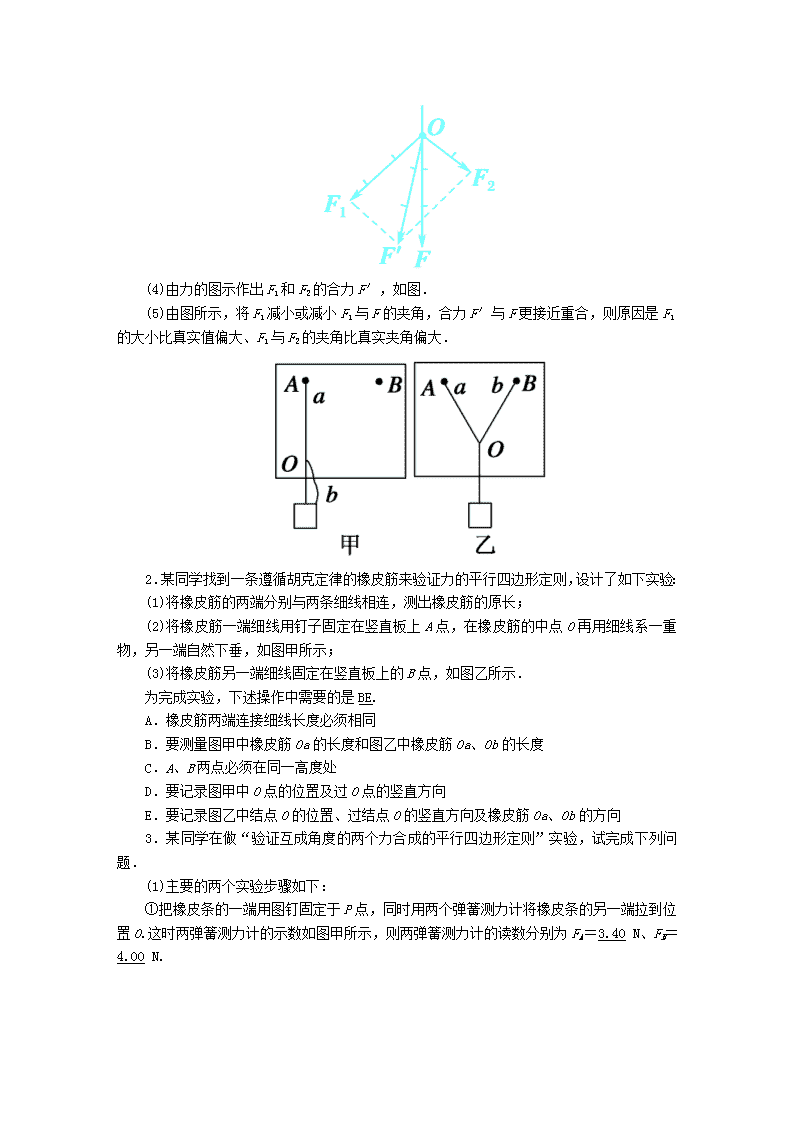2)将橡皮筋一端细线用钉子固定在竖直板上A点，在橡皮筋的中点O再用细线系一重物，另一端自然下垂，如图甲所示；‎ ‎(3)将橡皮筋另一端细线固定在竖直板上的B点，如图乙所示．‎ 为完成实验，下述操作中需要的是BE.‎ A．橡皮筋两端连接细线长度必须相同 B．要测量图甲中橡皮筋Oa的长度和图乙中橡皮筋Oa、Ob的长度 C．A、B两点必须在同一高度处 D．要记录图甲中O点的位置及过O点的竖直方向 E．要记录图乙中结点O的位置、过结点O的竖直方向及橡皮筋Oa、Ob的方向 ‎3．某同学在做“验证互成角度的两个力合成的平行四边形定则”实验，试完成下列问题．‎ ‎(1)主要的两个实验步骤如下：‎ ‎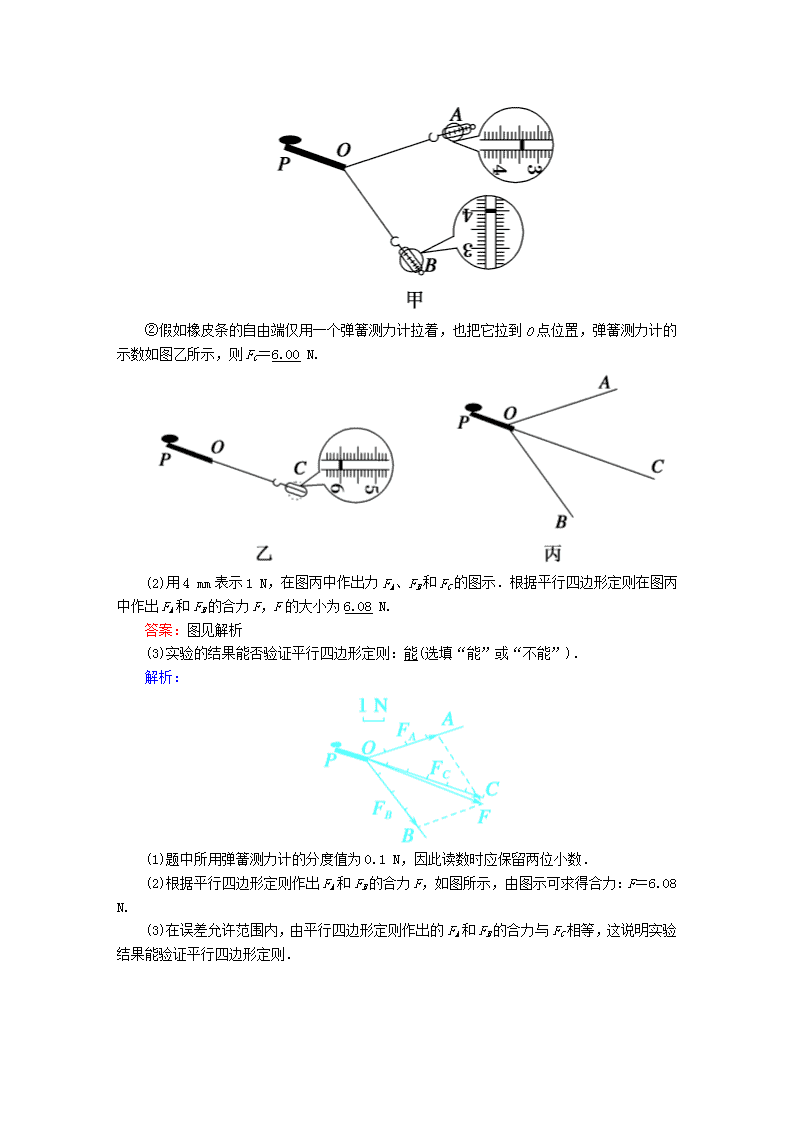①把橡皮条的一端用图钉固定于P点，同时用两个弹簧测力计将橡皮条的另一端拉到位置O.这时两弹簧测力计的示数如图甲所示，则两弹簧测力计的读数分别为FA＝3.40 N、FB＝4.00 N.‎ ‎②假如橡皮条的自由端仅用一个弹簧测力计拉着，也把它拉到O点位置，弹簧测力计的示数如图乙所示，则FC＝6.00 N.‎ ‎(2)用‎4 mm表示1 N，在图丙中作出力FA、FB和FC的图示．根据平行四边形定则在图丙中作出FA和FB的合力F，F的大小为6.08 N.‎ 答案：图见解析 ‎(3)实验的结果能否验证平行四边形定则：能(选填“能”或“不能”)．‎ 解析：‎ ‎(1)题中所用弹簧测力计的分度值为0.1 N，因此读数时应保留两位小数．‎ ‎(2)根据平行四边形定则作出FA和FB的合力F，如图所示，由图示可求得合力：F＝6.08 N.‎ ‎(3)在误差允许范围内，由平行四边形定则作出的FA和FB的合力与FC相等，这说明实验结果能验证平行四边形定则．‎ ‎4．用如图所示的器材和方法可以验证“力的平行四边形定则”．在圆形桌子透明桌面上平铺一张白纸，在桌子边缘安装三个光滑的滑轮，其中，滑轮P1固定在桌子边，滑轮P2、P3可沿桌边移动．‎ 第一次实验中，步骤如下：‎ A．在三根轻绳下挂上一定数量的钩码，并使结点O静止；‎ B．在白纸上描下O点的位置和三根绳子的方向，以O点为起点，作出三拉力的图示；‎ C．以绕过P2、P3绳的两个力为邻边作平行四边形，作出O点为起点的平行四边形的对角线，量出对角线的长度；‎ D．检验对角线的长度和绕过P1绳拉力的图示的长度是否一样，方向是否在一条直线上．‎ ‎(1)这次实验中，若一根绳挂的钩码质量为m，另一根绳挂的钩码质量为‎2m，则第三根绳挂的质量一定大于m且小于‎3m.‎ ‎(2)第二次实验时，改变滑轮P2、P3的位置和相应绳上钩码的数量，使结点平衡，绳的结点不必(选填“必须”或“不必”)与第一次实验中白纸上描下的O点重合．实验中，若桌面不水平不会(选填“会”或“不会”)影响实验的结论．‎ 解析：(1)若一根绳挂的钩码质量为m，另一根绳挂的钩码质量为‎2m，则两绳子的拉力分别为mg、2mg，两绳子拉力的合力F的范围是|2mg－mg|≤F≤mg＋2mg，即mg≤F≤3mg，三力的合力为零，则第三根绳挂的质量范围在m～‎3m之间，即第三根绳挂的质量一定大于m且小于‎3m.‎ ‎(2)本实验不是先用一根绳拉，然后用两根绳去拉，使一根绳拉的作用效果与两根绳拉的作用效果相同，而是三根绳都同时拉O点，所以O点的位置可以改变，若桌面不水平，也不会影响实验结论．‎ ‎5．图甲是“验证力的平行四边形定则”的实验装置．实验操作如下：‎ ‎(1)弹簧测力计A挂于固定点P，下端用细线挂一重物M，测量M(重物)的重力，并记录为F.‎ ‎(2)弹簧测力计B的一端用细线系于O点，手持另一端向左拉，使结点O静止在某位置(如图所示)，此时需记下结点O的位置和两测力计的示数F1、F2以及细线Oa、Ob、Oc的方向(或三段细线的方向)．‎ ‎(3)某同学已在图乙纸上作出F1、F2的图示，请根据力的平行四边形定则作出F1、F2的合力F′.‎ 答案：如图所示 ‎(4)改变两细线的夹角，重复做几次实验．若F′的方向近似在细线Oc方向上，且大小近似等于F，则平行四边形定则得以验证．‎ ‎6．(2018·天津理综)某研究小组做“验证力的平行四边形定则”实验，所用器材有：方木板一块，白纸，量程为5 N的弹簧测力计两个，橡皮条(带两个较长的细绳套)，刻度尺，图钉(若干个)．‎ ‎①具体操作前，同学们提出了如下关于实验操作的建议，其中正确的有BC.‎ A．橡皮条应和两绳套夹角的角平分线在一条直线上 B．重复实验再次进行验证时，结点O的位置可以与前一次不同 C．使用测力计时，施力方向应沿测力计轴线；读数时视线应正对测力计刻度 D．用两个测力计互成角度拉橡皮条时的拉力必须都小于只用一个测力计时的拉力 ‎②该小组的同学用同一套器材做了四次实验，白纸上留下的标注信息有结点位置O、力的标度、分力和合力的大小及表示力的作用线的点，如下图所示．其中对于提高实验精度最有利的是B.‎ 解析：①本实验中对所作的力的平行四边形没有特殊的要求，因此不需要让橡皮条与两细绳套夹角的角平分线在一条直线上，选项A错误；进行另一次验证时，O点位置可以改变，选项B正确；根据弹簧测力计的使用规则和读数规则可知选项C正确；实验不要求分力一定比合力小，选项D错误．‎ ‎②A图中，点与点的间距过小、两分力之间的夹角过小且标度过大，选项A错误；C图中，在测力计量程范围内，力过小，会导致读数误差较大，选项C错误；D图中，两个分力之间的夹角过小，同时标度过大，选项D错误；综上分析，只有选项B最有利于减小实验误差，选项B正确．‎ ‎7．某同学通过下述实验验证力的平行四边形定则．‎ 实验步骤：‎ ‎①将弹簧秤固定在贴有白纸的竖直木板上，使其轴线沿竖直方向．‎ ‎②如图甲所示，将环形橡皮筋一端挂在弹簧秤的秤钩上，另一端用圆珠笔尖竖直向下拉，直到弹簧秤示数为某一设定值时，将橡皮筋两端的位置标记为O1、O2，记录弹簧秤的示数F，测量并记录O1、O2间的距离(即橡皮筋的长度l)．每次将弹簧秤示数改变0.50 N，测出所对应的l，部分数据如表所示：‎ F/N ‎0‎ ‎0.50‎ ‎1.00‎ ‎1.50‎ ‎2.00‎ ‎2.50‎ l/cm l0‎ ‎10.97‎ ‎12.02‎ ‎13.00‎ ‎13.98‎ ‎15.05‎ ‎③找出②中F＝2.50 N时橡皮筋两端的位置，重新标记为O、O′，橡皮筋的拉力记为FOO′.‎ ‎④在秤钩上涂抹少许润滑油，将橡皮筋搭在秤钩上，如图乙所示．用两圆珠笔尖成适当角度同时拉橡皮筋的两端，使秤钩的下端达到O点，将两笔尖的位置标记为A、B，橡皮筋OA段的拉力记为FOA，OB段的拉力记为FOB.‎ 完成下列作图和填空：‎ ‎(1)利用表中数据在给出的坐标纸上画出Fl图线，根据图线求得l0＝10.00(9.80、9.90、10.10均正确) cm.‎ 答案：如图所示 ‎(2)测得OA＝‎6.00 cm，OB＝‎7.60 cm，则FOA的大小为1.80(1.70～1.90均正确) N.‎ ‎(3)根据给出的标度，作出FOA和FOB的合力F′的图示．‎ 答案：如图所示 ‎(4)通过比较F′与FOO′的大小和方向，即可得出实验结论．‎ 解析：(1)F－l图线的横轴截距表示F＝0时橡皮筋l的值，因此F－l图线的横轴截距即表示橡皮筋原长，l0＝‎10.0 cm.‎ ‎(2)橡皮筋总长度l＝‎6.00 cm＋‎7.60 cm＝‎13.60 cm，在F－l图线上找到与‎13.60 cm对应的弹力F＝1.80 N.‎ ‎(3)根据平行四边形定则，作出平行四边形并求出对角线表示的力F′.‎ ‎(4)因为F′是根据平行四边形定则求出的，FOO′是实际测量出的，如果在误差允许范围内，F′与FOO′近似相等，就验证了平行四边形定则．‎