2020-2021年新高二物理开学摸底考试卷（二） 20页

2020-2021 年新高二物理开学摸底考试卷（二） 一．选择题(本题共 12 小题;每小题 4 分,共 48 分。其中 1-8 题为单选题，9-12 为多选题，全部选对得 4 分，选对但不全得 2 分) 1.一个系统的机械能增大，究其原因，下列推测正确的是( ) A.可能是重力对系统做了功 B.一定是合外力对系统做了功 C.一定是系统克服合外力做了功 D.可能是摩擦力对系统做了功 解析 只有重力做功，系统的机械能守恒，选项 A 错误；除重力、弹力之外的力做正功时，系统机械能增 加，做负功时则减少，故选项 B、C 错误；如果摩擦力对系统做正功，则系统机械能增加，故选项 D 正确。 答案 D 2.如图所示，质量相等的 A、B 两物体随竖直圆筒一起做匀速圆周运动，且与圆筒保持相对静止，下列说法 中正确的是（ ） A. 线速度 ABvv B. 运动周期 ABTT C. 筒壁对它们的弹力 ABNN D. 它们受到的摩擦力 ABff 【答案】D 【解析】A、A 和 B 共轴转动，角速度相等即周期相等，由 v=rω 知，A 转动的半径较小，则 A 的线速度较 小，故 A、B 错误．C、A 和 B 做圆周运动靠弹力提供向心力，由 N=mrω2 知，A 的半径小，则 ABNN ； 竖直方向上：重力和静摩擦力平衡，重力相等，则摩擦力相等，即 fA=fB，故它们受到的合力 FA 合mb，它们的初动能相同，若 a 和 b 分别受到不变的阻 力 Fa 和 Fb 的作用，经过相同的时间停下来，它们的位移分别为 sa 和 sb，则( ) A.Fasb B.Fa>Fb，sa>sb C.Fa>Fb，samb，所以 saFb，故选项 C 正确。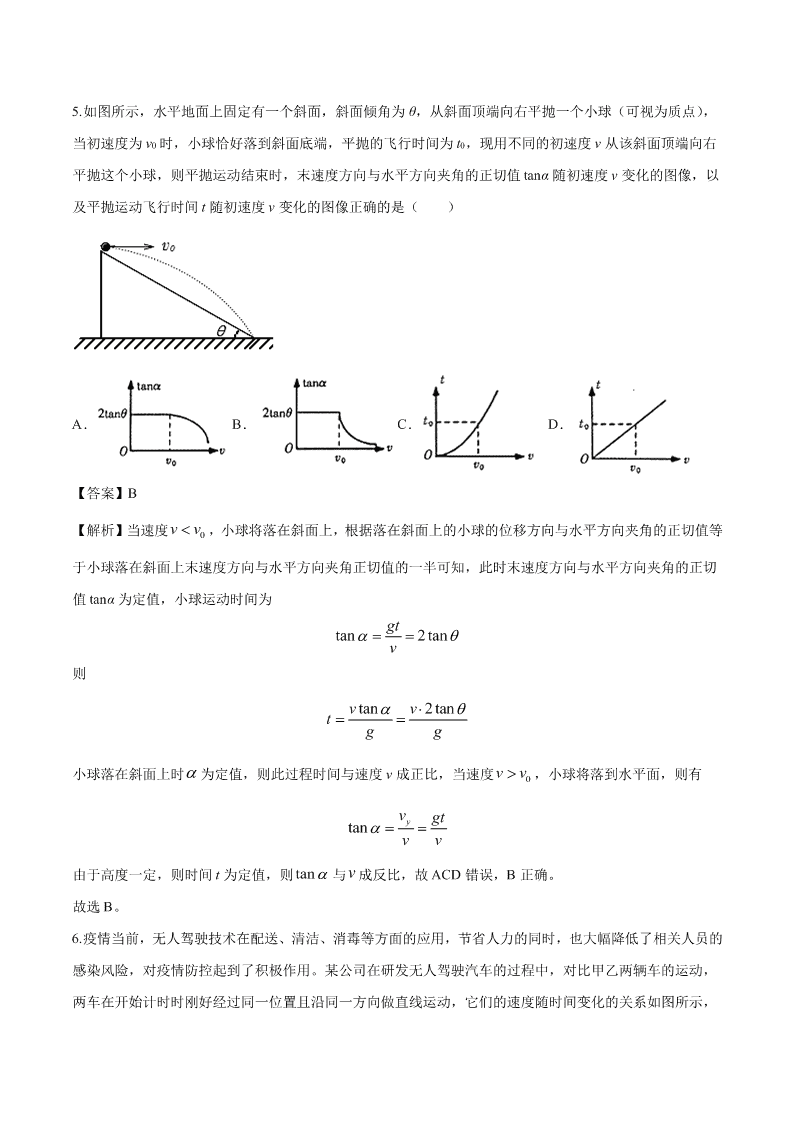 答案 C 5.如图所示，水平地面上固定有一个斜面，斜面倾角为 θ，从斜面顶端向右平抛一个小球（可视为质点）， 当初速度为 v0 时，小球恰好落到斜面底端，平抛的飞行时间为 t0，现用不同的初速度 v 从该斜面顶端向右 平抛这个小球，则平抛运动结束时，末速度方向与水平方向夹角的正切值 tanα 随初速度 v 变化的图像，以 及平抛运动飞行时间 t 随初速度 v 变化的图像正确的是（ ） A． B． C． D． 【答案】B 【解析】当速度 0vv ，小球将落在斜面上，根据落在斜面上的小球的位移方向与水平方向夹角的正切值等 于小球落在斜面上末速度方向与水平方向夹角正切值的一半可知，此时末速度方向与水平方向夹角的正切 值 tanα 为定值，小球运动时间为 tan2 tangt v 则 tan 2tanvvt gg  小球落在斜面上时 为定值，则此过程时间与速度 v 成正比，当速度 0vv ，小球将落到水平面，则有 tan yv gt vv  由于高度一定，则时间 t 为定值，则 tan 与v 成反比，故 ACD 错误，B 正确。 故选 B。 6.疫情当前，无人驾驶技术在配送、清洁、消毒等方面的应用，节省人力的同时，也大幅降低了相关人员的 感染风险，对疫情防控起到了积极作用。某公司在研发无人驾驶汽车的过程中，对比甲乙两辆车的运动， 两车在开始计时时刚好经过同一位置且沿同一方向做直线运动，它们的速度随时间变化的关系如图所示， 由图可知（ ） A．在 t = 3s 时，两车第一次相距最远 B．甲车任何时刻加速度大小都不为零 C．在 t = 6s 时，两车又一次经过同一位置 D．甲车 t = 6s 时的加速度与 t= 9s 时的加速度相同 【答案】A 【解析】A．甲乙两车同时同地出发，0 3s 内甲车速度大于乙车速度，甲在前乙在后，距离越来越远，3 6s 内甲车速度小于乙车速度，距离越来越近，所以 3st  时，甲乙两车速度相等，第一次距离最远，A 正确； B． vt 图像斜率的物理意义为加速度，图像的斜率可以为 0，所以甲车的加速度可以为 0，B 错误； C．图像与横轴所围面积代表位移，可知前 6s 内，乙的位移比甲的大，故 C 错误； D．甲车在 6s 时和 9s 时加速度方向不同，D 错误。故选 A。 7.一辆汽车的质量为 m，额定功率为 P，在保持额定功率不变的情况下，汽车启动时的 v-t 图象如图所示。 已知 1t 时刻的速度为 1v ， 2t 时刻的速度为 2v ，且 时刻的加速度为 时刻的加速度的 2 倍。若汽车所受阻 力大小恒定，则下列说法正确的是（ ） A. 汽车在 时刻的加速度为 21 1 12 2()P vva mv v  B. 汽车在 12tt 时间内的平均速率等于 12 2 vv C. 汽车能达到的最大速度为 12 1 212 vvy vv D. 汽车所受的恒定阻力为 21 23PP vv 【答案】A 【解析】B．t1-t2 时间内汽车做加速度减小的加速运动，由图象的“面积”表示位移知，其位移大于匀加速直 线运动的位移，则平均速度大于 12 2 vv ，故 B 错误； D．由题意，设 t 1 时刻的加速度为 a1、 2 时刻的加速度为 a2，根据牛顿第二定律有 1 1 P f m av  ， 2 2 P f m av  ， 122aa 联立解得 21 2 PPf vv 故 D 错误； C．汽车能达到最大速度时，则有 F=f，P=Fv 故 12 122 vvv vv  故 C 错误； A．根据 解得 21 1 12 2()P vva mv v  故 A 正确。故选 A。 8.如图所示，有一光滑轨道 ABC，AB 部分为半径为 R 的1 4圆弧，BC 部分水平，质量均为 m 的小球 a、b 固 定在竖直轻杆的两端，轻杆长为 R，不计小球大小。开始时 a 球处在圆弧上端 A 点，由静止释放小球和轻 杆，使其沿光滑轨道下滑，则下列说法正确的是( ) A.a 球下滑过程中机械能保持不变 B.b 球下滑过程中机械能保持不变 C.a、b 球滑到水平轨道上时速度大小为 2gR D.从释放 a、b 球到 a、b 球滑到水平轨道上，整个过程中轻杆对 a 球做的功为mgR 2 解析 a、b 球和轻杆组成的系统机械能守恒，选项 A、B 错误；由系统机械能守恒有 mgR＋mg·2 R＝1 2×2 mv2， 解得 a、b 球滑到水平轨道上时速度大小为 v＝ 3gR，选项 C 错误；从释放 a、b 球到 a、b 球滑到水平轨道 上，对 a 球，由动能定理有 W＋mgR＝1 2mv2，解得轻杆对 a 球做的功为 W＝mgR 2 ，选项 D 正确。 答案 D 9..如图所示，光滑斜槽固定在水平地面上，一小球从其顶端由静止开始下滑，取地面为零势能面。下滑过 程中，小球的速率 v、运动时间 t、动能 Ek、重力势能 EP、离地面的高度 h，它们之间的关系图像可能正确 的有（ ） A. B. C. D. 【答案】BD 【解析】A．设小球所在位置的切线与水平方向的夹角为  ，根据牛顿第二定律有 sinmg ma  解得 sinag  ，小球往下运动， 变小，则sin 变小，加速度变小，故小球向下做加速度不断减小的加 速运动，故 A 错误； BC．设刚开始小球离地高度为 H，下落一段时间离地高度为 h，小球向下运动过程中，只有重力做功，根 据机械能守恒定律有  kE mg H h 解得 kE m g H m g h 又 2 k 1 2E mv 解得 2 22v gH gh 故 B 正确，C 错误； D．离地高度为 h 时，重力势能为 pEmgh 故 D 正确。故选 BD。 10.2018 年 4 月 2 日，中国首个空间实验室“天宫一号”坠入大气层焚毁．天宫一号是中国首个“目标飞行器”， 其主要目的在于和神舟飞船（称“追踪飞行器”）配合完成交会对接飞行测试，为建设空间站积累经验．其在 轨工作 1630 天，失联 759 天，在地球引力下轨道高度不断衰减，最终于 4 月 2 日早晨 8 点 15 分坠入大气 层焚毁．据报道，该次坠落没有造成任何危险．天宫一号空间实验室于 2011 年 9 月 29 日在酒泉发射升空， 设计寿命两年，轨道平均高度约为 350km．作为中国空间站的前身，在役期间，天宫一号先后与神舟八号、 九号、十号飞船配合完成六次交会对接任务，共计接待 6 名航天员，完成多项科学实验．设“天宫一号”飞行 器的轨道半径为 r，地球表面重力加速度为 g，地球半径为 R，地球自转周期为 T，对于“天宫一号”在服役 运行过程中，下列说法正确的是 A．根据题中数据，可求出地球的质量 23 2 4 rM GT  ， 地球质量也可表达为 2gRM G B．“神州八号”飞船与“天宫一号”进行对接时，“神州八号”飞船需要从低轨道加速 C．“天宫一号”飞行器运动的周期是 0 2 rT g D．天宫一号的航天员在一天内可以看到日出的次数是 2 32 T gRN r 【答案】BD 【解析】A．根据 2 22 4MmG m rrT  宫一 因天宫一号的周期未知，题中给出的是地球自转周期，则不能求解地球质量，可根据 2 MmG mgR  求解地球质量 2gRM G 选项 A 错误； B．“神州八号”飞船与“天宫一号”进行对接时，“神州八号”飞船需要从低轨道加速，然后进入高轨道实现对 接，选项 B 正确； C．根据 2 22 0 4MmGmrrT  可知“天宫一号”飞行器运动的周期是 33 222rrT GM gR == 选项 C 错误； D．天宫一号的航天员每转一周即可看到一次日出，一天转的圈数是 2 3 0 2 T T gRN Tr 则在一天内可以看到日出的次数是 选项 D 正确； 故选 BD. 11.滑板运动是以滑行为特色、崇尚自由的一种运动，深受都市青年的喜爱。滑板的一种运动情境可简化为 如下模型：如图甲所示，将运动员（包括滑板）简化为质量 5 0 k gm  的物块，物块以某一初速度 0v 从倾角 37  的斜面底端冲上足够长的斜面，取斜面底端为重力势能零势能面，该物块的机械能 E总 和重力势能 pE 随离开斜面底端的高度 h 的变化规律如图乙所示。将物块视为质点，重力加速度 210m / s ，则由图中数据可 得（ ） A．初速度 0 5 m/ sv  B．物块与斜面间的动摩擦因数为 0.3 C．物块在斜面上运动的时间为 4 s3 D．物块再次回到斜面底端时的动能为 375J 【答案】AD 【解析】A．斜面底端为重力势能零势能面，则 2 01 1 625J2Emv总 得 0 5m/sv  故 A 正确； B．当 pEE总 时，物块运动到最高点由图乙可知此时 m 1mh  根据功能关系，有 mcos125Jsin hmgE  总 得物块与斜面间动摩擦因数 3 16  故 B 错误； CD．物块沿斜面上滑的时间 0 1 2 ssincos3 vt gg 上滑的位移 m 5 ms i n 3 hs  因为 tan ，所以物块最终会沿斜面下滑，下滑的 2 2215 sincos9 st gg 物块在斜面上运动的时间为 12 6215 s9t tt  滑到斜面底端时的动能 m k 1 2cos375J sin hEEmg 总 故 C 错误，D 正确。故选 AD。 12.如图所示，质量 M 的小球套在固定倾斜的光滑杆上，原长为 l0 的轻质弹簧一端固定于 O 点，另一端与小 球相连，弹簧与杆在同一竖直平面内．图中 AO 水平，BO 间连线长度恰好与弹簧原长相等，且与杆垂直， O′ 在 O 的正下方，C 是 AO′段的中点，θ＝30°．现让小球从 A 处由静止释放，下列说法正确的有 A．下滑过程中小球的机械能守恒 B．小球滑到 B 点时的加速度为 3 2 g C．小球下滑到 B 点时速度最大 D．小球下滑到 C 点时的速度为 02gl 【答案】BD 【解析】A、下滑过程中小球的机械能会和弹簧的弹性势能相互转化，因此小球的机械能不守恒，故 A 错 误； B、因为在 B 点，弹簧恢复原长，因此重力沿杆的分力提供加速度，根据牛顿第二定律可得 c o s3 0m g m a  解得 3 2ag 故 B 正确； C、到达 B 点加速度与速度方向相同，因此小球还会加速，故 C 错误； D、因为 C 是 AO′段的中点，θ＝30°，所以当小球到 C 点时，弹簧的长度与在 A 点时相同，故在从 A 到 C 的过程中弹簧弹性势能没变，小球重力做功全部转化为小球的动能，所以得 2 0 1 2 cm g l m v 解得 02cvgl 故 D 正确。 第 II 卷（非选择题) 二．实验题：(本题共 2 小题,共 14 分） 13.（6 分）用如图所示的甲、乙两种装置都可以进行“探究做功与物体速度变化的关系”实验。 (1)a、b 是两个实验中打出的纸带的一部分，A、B、C、…、G 是纸带上标出的计数点，每两个相邻的计数 点之间还有 4 个打出的点未画出。其中图____（填“a”或“b”）所示的是用乙装置的实验纸带。用甲装置实验 时打下 F 点的瞬时速度 v=____m/s（保留 2 位有效数字）。 (2)在用乙装置进行的实验中，平衡阻力后，小车与橡皮筋组成的系统在橡皮筋恢复形变前机械能___（填“守 恒”或“不守恒”）。 【答案】a 0.28 不守恒 【解析】(1)[1]甲图装置是恒力拉动小车做匀加速直线运动，体现相等时间内的位移差恒定，对应纸带 b， 乙装置是橡皮筋的弹力拉动小车，是逐渐减小的弹力作用，小车应先做变加速度直线运动后做匀速直线运 动，对应纸带 a； [2]甲装置对应纸带 b，相邻计数点间有四个点未画出，则时间间隔为 0.025s0.1sT  由匀变速直线运动的推论，平均速度等于中间时刻的瞬时速度，有 2(2.603.00)10 m/s0.28m/s220.1 EG F xv T   (2)[3]小车与橡皮筋组成的系统有重力做正功，橡皮筋的弹力做正功，摩擦力做负功，则即使平衡了摩擦力， 依然有除重力和弹力之外的摩擦力做负功，系统的机械能减少，机械能不守恒。 14.（8 分）用如图所示装置可验证机械能守恒定律，轻绳两端系着质量相等的物块 A、B，物块 B 上放一金 属片 C，铁架台上固定一金属圆环，圆环处在物块 B 的正下方。开始时，金属片 C 与圆环间的高度为 h，A、 B、C 由静止开始运动。当物块 B 穿过圆环时，金属片 C 被搁置在圆环上，两光电门分别固定在铁架台 P1、 P2 处，通过数字计时器可测出物块 B 从 P1 旁运动到 P2 旁所用时间 t，已知重力加速度为 g。 (1)若测得 P1、P2 之间的距离为 d，则物块 B 刚穿过圆环后的速度v  ________。 (2)若物块 A、B 的质量均用 M 表示，金属片 C 的质量用 m 表示，该实验中验证了下面选项________中的等 式成立，即可验证机械能守恒定律。 A． 21 2mghMv B． 2m g h M v C．   21 22mghMmv D．   21 2mghMmv (3)改变物块 B 的初始位置，使物块 B 从不同的高度由静止下落穿过圆环，记录每次金属片 C 与圆环间的高 度 h 以及物块 B 从 P1 旁运动到 P2 旁所用时间 t，则以 h 为纵轴，以________ ( 选填“ 2t ”或“ 2 1 t ”）为横轴， 通过描点作出的图线是一条过原点的直线，该直线的斜率 k  ________ 用 m、g、M、d 表示 ) 。 【答案】 d t C 2(2 ) 2 M m d mg  【解析】(1)[1]根据平均速度等于瞬时速度，则有物块 B 刚穿过圆环后的速度 dv t (2)[2]由题意可知，系统 ABC 减小的重力势能转化为系统的增加的动能，即为 21 (2 )2mgh Mgh Mgh M m v    即为 2 2 2 11(2)(2)22 dmghMm vMm t 故 C 正确，ABD 错误。 故选 C。 (3)[3][4]将 21 22mghMmv() 变形后则有 22 2 (2)(2) 22 Mm vMm dh mgmgt  因此以 为横轴；由上式可知，作出的图线是一条过原点的直线，直线的斜率 2(2) 2 Mm dk mg  三．解答题：共 4 个⼩题，共 38 分。应写出必要的文字说明、方程式和重要的演算步骤，只写出最后 答案的不能得分，有数值计算的题必须明确写出数据值和单位。 15.（8 分）消防员半夜接到火情报警后，常常利用一根固定的竖直金属杆从楼上的宿舍下滑到楼下的消防 车附近，用最短的时间出警，如图所示，某队员在顶端握住杆由静止开始滑下，先做匀加速直线运动，再 做匀减速直线运动。加速过程的加速度大小是减速过程的加速度大小的 2 倍。下滑过程共用时 1.5s，下滑了 3m，速度减小至零（此时人未接触地面）。人的质量为 60kg，g 取 210m/s 。求： (1)人开始下滑前，杆对人的摩擦力； (2)人下滑过程中的最大速度； (3)匀加速运动的加速度大小。 【答案】(1)600N，方向竖直向上；(2)4m/s；(3)8m/s2 【解析】(1)人开始下滑前，对人受力分析：人竖直方向受到重力和摩擦力，由平衡条件得杆对人的摩擦力 为 600NFmg 方向竖直向上 (2)设人下滑过程中的最大速度为 vm，由题意可得 2 mvxt 解得 22 3 m/s4m/s3 2 m xv t  (3)由题意得匀加速运动过程有 11mva t 匀减速过程有 220 mv a t 据题有 122aa 121 . 5 stt 联立解得 2 1 8m/sa  16.（10 分）我国将在 2013 年使用长征三号乙火箭择机发射嫦娥三号．发射嫦娥三号是采用火箭喷气发动 机向后喷气而加速的．设运载火箭和嫦娥三号的总质量为 m，地面附近的重力加速度为 g，地球半径为 R， 引力常量为 G。 （1）用题给物理量表示地球的质量。 （2）假设在嫦娥三号舱内有一平台，平台上放有测试仪器，仪器对平台的压力可通过监控装置传送到地 面．火箭从地面启动后竖直向上做加速直线运动，升到距离地面高度等于地球半径的 1 2 时，地面监控器显 示测试仪器对平台的压力为启动前压力的 17 18 ，求此时火箭的加速度。 【答案】（1） 2gRM G ；（ 2） 2 ga  【解析】（1）根据在地面附近重力和万有引力相等，则有 2 MmGmgR  ① 解得 ② （2）取测试仪为研究对象 起飞前，由物体的平衡条件得 1 2N MmFGR ③ 升到距离地面高度等于地球半径的 时，牛顿第二定律得 2 2()2 N MmFGma RR   ＝ ④ 由题意知 2 1 17 18 N N F F  ⑤ 由①③④⑤解得： 2 ga  17.（10 分）.学校物理社团为研究“竖直平面内圆周运动的临界速度大小”，设计了如下实验装置。 如图甲 所示，光滑圆轨道固定在竖直平面内，质量为 m 的小球从轨道最高点以初速度 v0 开始运动，已知轨道半径 为 R，重力加速度为 g，请回答： (1)若小球初速度 0 2v gR ，则最高点 A 处小球对轨道的弹力大小为多少； (2)如图乙所示，将一轻质弹簧一端固定在 AO 中点 P 处，另一端与小球相连接，弹簧原长为 R，劲度系数 mgk R ，小球运动过程中弹簧始终在竖直平面内，弹簧可绕 P 点无摩擦转动，为使小球不脱离轨道，则在 最高点速度至少多大； (3)在(2)问结果下，小球到达最低点 B 处时所受轨道弹力大小为多少。 【答案】（1） mg ；（ 2） 2 gR ；（ 3）5mg 【解析】（1）小球在最高点的合力提供向心力，则有 2 0 NAF vmgm R 解得 NAFmg （2）由胡克定律得，弹簧弹力 1 2 mgF k x   方向向上 小球恰好通过轨道最高点有 0NAF  ，则在高点根据牛顿第二定律有 2 1 Avm g F m R 解得 2A gRv  （3）由题意知，从最高点运动至最低点的过程，小球和弹簧构成的系统机械能守恒，以最低点为零势能面， 弹簧在 A、B 处形变量相同，则有 p A p BEE 根据系统机械能守恒，则有 22112022ApABpBmgRmvEmvE B 处弹簧弹力大小为 2 2 mgF  ，方向向上，在 B 点，根据牛顿第二定律有 2 2 B NB vFFmgm R 联立方程解得 5NBFmg 18.如图所示，在倾角为 θ=30°的光滑斜面 MN 底端固定一个被压缩且锁定的轻弹簧，轻弹簧的上端静止放 一质量 m=2kg 的滑块，且滑块与斜面顶端 N 点相距 x=0.10m。现将弹簧解除锁定，滑块离开弹簧后经 N 点 离开斜面，恰水平飞上顺时针始终匀速转动的传送带，已知传送带水平放置且足够长，传送带上端距 N 点 所在水平面高度为 h=0.20m，滑块 A 与传送带间的动摩擦因数 3 2  （g 取 10m/s2）。 (1)弹簧锁定时储存的弹性势能； (2)若传送带速度为 73m/s，求滑块飞上传送带后因摩擦产生的内能； (3)传送带右端竖直固定半径 R=0.1m 的光滑半圆轨道，且轨道下端恰好与传送带相切，为使滑块能沿半圆轨 道运动而不脱离半圆轨道，求传送带速度应当满足的条件。 【答案】(1)17J；(2)75J；(3) 2m /sv  或 5 m / sv  【解析】(1)滑块离开斜面后，竖直方向由 2 0 1 2h g t 得 0 0 . 2 st  所以滑块离开斜面时 0 0 tan 30gt v  ° 得 0 23m/sv  对滑块，从开始到恰上斜面 2 P0 1(sin 30) 2Emgxhmv ° 得 P 17JE  (2)滑块飞上传送带后，对滑块 mgma  得 25 3m/sa  由 0v v at传 得 1st  则 7 3 mx v t 传 传 2 0 1 9 3 m22x v t at  物 所以 53m2s 相 所以 75JQmgs相 (3)若滑块不能越过四分之一圆弧，对滑块 2 1 1 =2 m v m g R 则 1= 2m/sv 若滑块不能越过四分之一圆弧，在最高点对滑块 2 Qvmgm R 得 Q 1m/sv  从最低点到最高点，对滑块 22 2Q 112+22mvmg Rmv 得 2 =5m/sv 所以传送带运行速度 1vv 或 2vv 即 2m /sv  或 5 m / sv  。