山东省枣庄三中2021届高三物理9月阶段试题（Word版带解析） 16页

‎2020—2021学年高三年级第一次质量检测 物理试题 第一卷（40分）‎ 一、选择题（共12题，其中1—8题为单选，每题3分；9—12题为多选，每题4分，选不全得2分）‎ ‎1. 在物理学研究过程中科学家们创造了许多物理学研究方法，如理想实验法、控制变量法、极限法、等效替代法、理想模型法、微元法等，以下关于所用物理学研究方法叙述错误的是(　　)‎ A. 根据速度定义式，当Δt非常小时，就可以表示物体在t时刻的瞬时速度，该定义采用了极限法 B. 加速度的定义式为，采用的是比值定义法 C. 在不需要考虑物体的大小和形状时，用质点来代替实际物体采用了等效替代的方法 D. 在推导匀变速直线运动位移公式时，把整个运动过程划分成很多小段，每一小段近似看做匀速直线运动，然后把各小段的位移相加，这里采用了微元法 ‎【答案】C ‎【解析】‎ ‎【详解】A. 为研究某一时刻或某一位置时的速度，我们采用了取时间非常小，即让时间趋向无穷小时的平均速度作为瞬时速度，即采用了极限思维法，故A正确；‎ B. 加速度的定义式为a=△v/△t，a与速度变化量以及时间无关，采用的是比值定义法，故B正确； ‎ C. 质点采用的科学方法为建立理想化的物理模型法，故C错误；‎ D. 在探究匀变速运动的位移公式时，采用了微元法将变速运动无限微分后变成了一段段的匀速运动，即采用了微元法；故D正确；‎ 本题选错误的，故选C ‎2. 如图，一质点从A点开始做初速度为零的匀加速直线运动，加速度大小为a，B、C、D是质点运动路径上三点，且BC＝x1，CD＝x2，质点通过B、C间所用时间与经过C、D间所用时间相等，则质点经过C点的速度为(　　)‎ A. B. ‎ C. D. 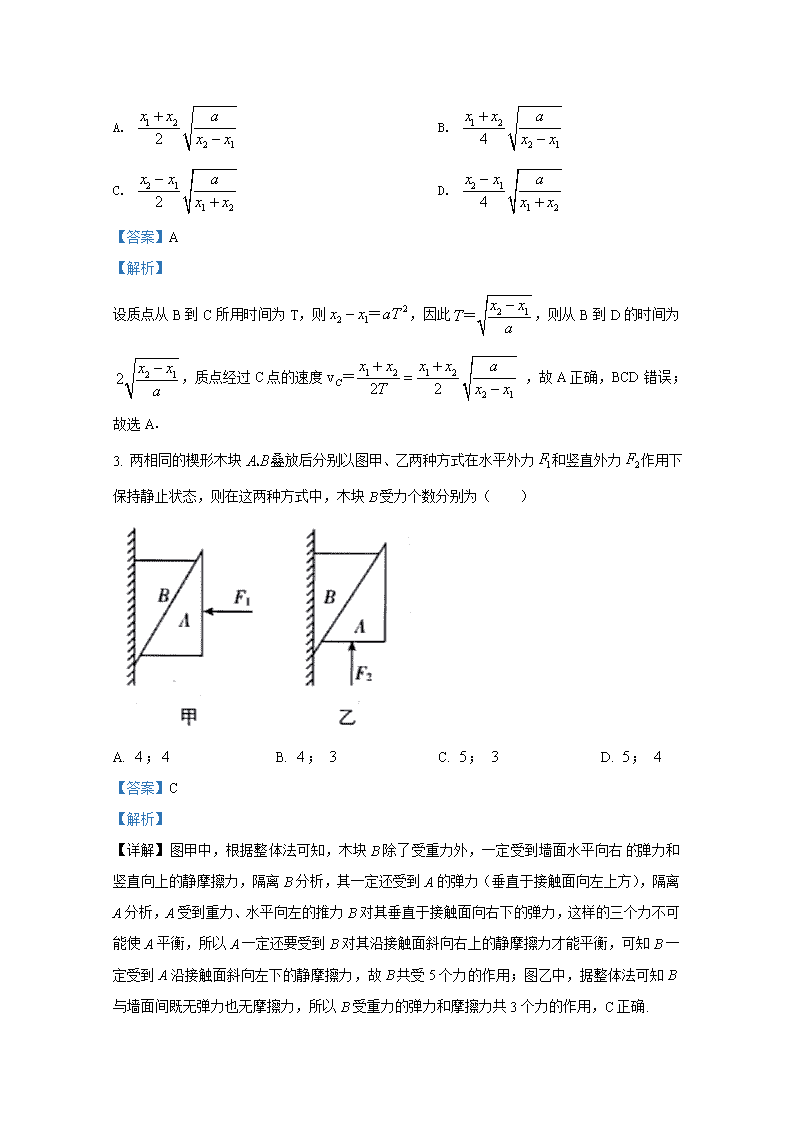‎ ‎【答案】A ‎【解析】‎ 设质点从B到C所用时间为T，则，因此，则从B到D的时间为，质点经过C点的速度 ，故A正确，BCD错误；故选A．‎ ‎3. 两相同的楔形木块叠放后分别以图甲、乙两种方式在水平外力和竖直外力作用下保持静止状态，则在这两种方式中，木块受力个数分别为（ ）‎ A. ； B. ； C. ； D. ； ‎ ‎【答案】C ‎【解析】‎ ‎【详解】图甲中，根据整体法可知，木块B除了受重力外，一定受到墙面水平向右弹力和竖直向上的静摩擦力，隔离B分析，其一定还受到A的弹力（垂直于接触面向左上方），隔离A分析，A受到重力、水平向左的推力B对其垂直于接触面向右下的弹力，这样的三个力不可能使A平衡，所以A一定还要受到B对其沿接触面斜向右上的静摩擦力才能平衡，可知B一定受到A沿接触面斜向左下的静摩擦力，故B共受5个力的作用；图乙中，据整体法可知B与墙面间既无弹力也无摩擦力，所以B受重力的弹力和摩擦力共3个力的作用，C正确.‎ ‎4. 如图所示，用三根细线a、b、c将两个小球1和2悬挂起来，静止在竖直面内，已知两球重均为G，细线a与竖直方向夹角为30°，细线c水平．关于三根细线a、b、c的拉力Ta、Tb、Tc大小的比较正确的是 A. Ta一定小于Tb B. Ta一定大于Tc C. Ta可能小于Tc D. Tb可能小于Tc ‎【答案】B ‎【解析】‎ ‎【详解】A.对小球1受力分析，根据平衡状态可知，Ta等于Tb与重力的合力，因为Tb与重力夹角是锐角，所以Ta一定大于Tb，故A错误．‎ BC.将两小球看作一个整体，对整体受力分析，受力如图所示 根据共点力的平衡条件有：‎ 所以a绳拉力一定大于c绳拉力，故B正确C错误．‎ D.同理，Tb等于重力与Tc的合力大小，重力与Tc相互垂直，根据勾股定理可知，Tb大于Tc，故D错误．‎ ‎5. 如图所示A、B两个物体叠放在一起，静止在粗糙水平地面上，B与水平地面间的动摩擦因数μ1=0.1，A与B之间的动摩擦因数μ2=0.2．已知物体A的质量m=‎2kg，物体B的质量 M=‎3kg，重力加速度g取‎10m/s2．现对物体B施加一个水平向右的恒力F，为使物体A与物体B相对静止，则恒力的最大值是（物体间的最大静摩擦力等于滑动摩擦力）（　　）‎ A. 20N B. 15N C. 10N D. 5N ‎【答案】B ‎【解析】‎ 当F作用在物体B上时，A、B恰好不滑动则静摩擦力达到最大值，对物体A隔离分析，根据牛顿第二定律有：μ2mg=ma 对整体，根据牛顿第二定律有：Fmax-μ1（m1+m2）g=（m1+m2）a；联立以上各式解得：Fmax=15N，故B正确，ACD错误．‎ ‎6. 如图、在竖直墙壁的A点处有一根水平轻杆a,杆的左端有一个轻滑轮O.一根细线上端固定在该天花板的B点处,细线跨过滑轮O,下端系一个重为G的物体,开始时BO段细线与天花板的夹角为θ=.系统保持静止,当轻杆a缓慢向下移动的过程中,不计一切摩擦,下列说法中正确的是( )‎ A. 细线BO对天花板拉力不变 B. a杆对滑轮的作用力的方向沿杆水平向右 C. a杆对滑轮的作用力逐渐减小 D. 开始时绳对滑轮的作用力大小大于G ‎【答案】C ‎【解析】‎ ‎【详解】A.当轻杆a缓慢向下移动的过程中，细线的拉力大小始终等于物体的重力G，保持不变，但由于θ增大，所以细线BO对天花板的拉力方向发生改变，所以此拉力是变化的，故A项错误；‎ BC.两细线拉力大小不变，夹角增大，由它们的合力减小，根据滑轮平衡可知，a杆对滑轮的作用力与两细线的合力大小相等、方向相反，所以a杆对滑轮的作用力逐渐减小，a杆对滑轮 的作用力F的方向沿两夹平分线斜向右上方，如图 故B项错误，C项正确；‎ D.细绳BO、AO大小都等G，且两绳拉力夹角为，由平行四边形定则可知，合力为G，即开始时绳对滑轮的作用力大小等于G，故D项错误．‎ ‎7. 甲、乙两车在一平直公路上从同一地点沿同一方向沿直线运动，它们的v-t图像如图所示．下列判断不正确的是 A. 乙车启动时，甲车在其前方‎50m处 B. 乙车超过甲车后，两车不会再相遇 C. 乙车启动10s后正好追上甲车 D. 运动过程中，乙车落后甲车的最大距离为‎75m ‎【答案】C ‎【解析】‎ ‎【详解】A、根据速度图线与时间轴包围的面积表示位移，可知乙在时启动，此时甲的位移为，即甲车在乙前方‎50m处，故选项A正确；‎ B、乙车超过甲车后，由于乙的速度大，所以不可能再相遇，故选项B正确；‎ C、由于两车从同一地点沿同一方向沿直线运动，当位移相等时两车才相遇，由图可知，乙车启动10s后位移小于甲的位移，还没有追上甲，故选项C错误；‎ D、当两车的速度相等时相遇最远，最大距离为：，故选项D正确；‎ 不正确的是选选项C．‎ ‎8. 如图所示，质量为‎4kg的物体A静止在竖直的轻弹簧上面．质量为‎1kg的物体B用细线悬挂起来，A、B紧挨在一起但A、B之间无压力．某时刻将细线剪断，则细线剪断瞬间，B对A的压力大小为（g取l‎0m/s2）的（ ）‎ A. 0 B. 50N C. 10N D. 8N ‎【答案】D ‎【解析】‎ ‎【详解】剪断细线前，A、B间无压力，则弹簧的弹力F=mAg=40N，剪断细线的瞬间，对整体分析，整体加速度：，隔离对B分析，mBg-N=mBa，解得：N=mBg-mBa=10-1×2N=8N．故D正确，ABC错误．故选D．‎ ‎9. 在一次救灾活动中，一辆救灾汽车由静止开始做匀变速直线运动，刚运动了8 s，由于前方突然有巨石滚下，堵在路中央，所以又紧急刹车，匀减速运动经4 s停在巨石前．则关于汽车的运动情况，下列说法正确的是 A. 加速、减速中的加速度大小之比为a1∶a2等于2∶1‎ B. 加速、减速中的平均速度大小之比∶等于1∶1‎ C. 加速、减速中的位移大小之比x1∶x2等于2∶1‎ D. 加速、减速中的加速度大小之比a1∶a2不等于1∶2‎ ‎【答案】BC ‎【解析】‎ ‎【详解】AD．设加速阶段的末速度为v，则加速阶段的加速度大小为：‎ 减速阶段的加速度大小：‎ 则加速度大小之比为1：2，故A错误，D错误；‎ B．根据匀变速直线运动的平均速度公式：‎ 得加速阶段和减速阶段的平均速度之比为1：1．故B正确；‎ C．根据：‎ 知加速阶段和减速阶段的位移之比为2：1．故C正确．‎ ‎10. 如图所示，两个完全相同光滑小球P、Q，放置在墙壁和斜木板之间，当斜木板和竖直墙壁的夹角θ角缓慢减小时（ ），则（　　）‎ A. 墙壁、木板受到P球的压力均增大 B. 墙壁、木板受到P球的压力均减小 C. Q球对P球的压力增大，对木板的压力减小 D. P球受到墙壁、木板和Q球的作用力的合力不变 ‎【答案】ACD ‎【解析】‎ ‎【详解】AB、以小球P、Q为研究对象，处于平衡装态，根据受力平衡， ‎ 由图可知，墙壁对球的压力F2逐渐增大，木板对球的支持力F1逐渐增大，根据牛顿第三定律可知墙壁受到的压力增大，木板受到的压力增大，故A正确，B错误；‎ C、以小球Q为研究对象，处于平衡装态，根据受力平衡，P球对Q球的支持力，木板给Q球的支持力，当斜木板和竖直墙壁的夹角θ角缓慢减小时，P球对Q球的支持力增大，挡板给Q球的支持力减小，根据牛顿第三定律可知Q球对P球的压力增大，对木板的压力减小，故C正确；‎ D、小球P为研究对象，处于平衡装态，合外力为零，P球受到重力、墙壁对球的压力、木板对球的支持力和Q球对P球的压力，所以P球受到墙壁、木板和Q球的作用力的合力与P球受到重力大小相等，方向相反，故D正确；‎ 故选ACD．‎ ‎【点睛】对球进行正确受力分析，把握其受力特点：一个力大小和方向不变（重力），一个力方向不变（墙给球的支持力），另一个力的大小、方向均发生变化（挡板给球的作用力），对于这类动态平衡问题，可以采用“图解法”进行．‎ ‎11. 如图甲所示，倾角为θ的粗糙斜面体固定在水平面上，初速度为v0=‎10m/s、质量为m=‎1kg的小木块沿斜面上滑，若从此时开始计时，整个过程中小木块速度的平方随路程变化的关系图像如图乙所示，取g=‎10m/s2，下列说法正确的是（ ）‎ A. 0-5s内小木块做匀减速运动 B. 在t=1s时，摩擦力反向 C. 斜面倾角θ=37°‎ D. 小木块与斜面间的动摩擦因数为0.5‎ ‎【答案】BCD ‎【解析】‎ 由匀变速直线运动的速度位移公式：v2-v02=2ax与图象看的：，由图示图象可知，初速度：v02=100，v0=‎10m/s，减速运动时间：，故A错误；由图示图象可知，在0-1s内物体向上做匀减速运动，1s后物体反向做匀加速运动，t=1s时摩擦力反向，故B正确；由图示图象可知，物体 反向加速运动时的加速度： ，由牛顿第二定律得：mgsinθ+μmgcosθ=ma，mgsinθ-μmgcosθ=ma′，代入数据解得：μ=0.5，θ=37°，故D正确，C错误；故选BD．‎ ‎12. 如图所示，两根轻绳一端系于结点O，另一端分别系于固定圆环上的A、B两点，O点下面悬挂一物体M，绳OA水平，拉力大小为F1，绳OB与OA夹角α=120°，拉力大小为F2，将两绳同时缓慢顺时针转过60°，并保持两绳之间的夹角α始终不变，且物体始终保持静止状态。则在旋转过程中，下列说法正确的是（　　）‎ A. F1逐渐增大 B. F1先增大后减小 C. F2逐渐减小 D. F2先增大后减小 ‎【答案】AC ‎【解析】‎ ‎【详解】设两绳转动过程中，绳OA与水平方向的夹角为θ，以O点为研究对象，受力分析如图所示 因为两绳是缓慢移动的，所以O点始终处于平衡状态，由平衡条件得 由以上两式解得 当θ<60°时，θ增大，F1增大，F2减小，故AC正确，BD错误。‎ 故选AC。‎ 第二卷（60分）‎ 二、实验题（13题6分，14题6分，共计12分）‎ ‎13. 在用打点计时器“测定匀变速直线运动的加速度”实验中：‎ ‎(1)所用实验器材除电磁打点计时器（含纸带、复写纸）、小车、一端带有滑轮的长木板、绳、钩码、导线及开关外，在下面的器材中，必须使用的还有____（填选项代号）‎ A．电压合适的交流电源 B．电压合适的直流电源 C．刻度尺 D．停表 E．天平 ‎(2)某同学将打点计时器接到频率为50Hz的交流电源上，实验时得到一条纸带，纸带上O、A、B、C、D、E为计数点，每相邻两个计数点间还有4个点没有画出。‎ 由纸带可知，打C点时小车的速度______m/s（结果保留三位有效数字）‎ ‎(3)若实验时，电源频率略高于于50Hz，但该同学仍按50Hz计算小车的速度，则测量得到的小车速度与真实速度相比将___________（填“偏大”“偏小”或“不变”）。‎ ‎【答案】 (1). AC (2). 0.813 (3). 偏小 ‎【解析】‎ ‎【详解】(1)[1]打点计时器使用的是交流电源，测量点迹间的距离需要刻度尺，由于打点计时器可以记录时间，不需要秒表，该实验不需要测量钩码的质量，所以不需要天平 故选AC ‎(2)[2]打点的时间间隔为0.02s，由于相邻两计数点间还有四个打点未画出，则相邻两个计数点间所对应的时间T=0.1s，C点的瞬时速度为 ‎(3)[3]若实验时，电源频率略高于于50Hz，但该同学仍按50Hz计算，则计点周期偏大，则计 算小车的速度将偏小 ‎14. 某探究小组为了测定重力加速度，设计了如图甲所示的实验装置．工型挡光片悬挂于光电门的正上方，释放挡光片后，工型挡光片竖直下落，它的两臂A、B依次通过光电门，光电计时器记录A、B分别通过光电门的时间．‎ ‎（1）用图乙游标卡尺测量工型挡光片的两臂A、B的宽度d1和d2，某次用20分度的游标卡尺测量A的宽度d1时如图所示，则臂A的宽度d1为_____mm．‎ ‎（2）若计时器显示臂A、B通过光电门的时间分别为t1和t2，则臂A、B通过光电门的速度表达式分别为____、____．‎ ‎（3）若测得臂A、B之间的距离为L（L远大于d1、d2），用以上测量量表示当地重力加速度的表达式为____．‎ ‎【答案】 (1). （1）3.35， (2). （2） (3). (4). （3） ．‎ ‎【解析】‎ ‎【详解】（1）游标卡尺的主尺读数为‎3mm，游标读数为0.05×‎7mm=‎0.35mm，则最终读数为‎3.35mm ‎（2）极短时间内平均速度等于瞬时速度的大小，可知壁A通过光电门的速度，‎ ‎（3）根据速度位移公式得，，‎ 解得 三、计算题，本题包括5小题，共48分。解答应写出必要的文字说明、方程式和重要的演算步骤。只写出最后答案的不能得分，有数值计算的题，答案中必须明确写出数值和单位 ‎15. 如图所示，在水平场地中冰壶运动员从起点A用水平恒力推动静止的冰壶，一段时间后放手，让冰壶最后停在规定有效区域BC内，已知AB长L1=‎10m，BC长L2=‎1.25m．推力作用下冰壶（可视为质点）的加速度a1=‎8m/s2，冰壶与地面的摩擦因数为0.2，g取‎10m/s2，求：‎ ‎（1）放手后冰壶运动的加速度大小a2；‎ ‎（2）推力作用的最大距离．‎ ‎【答案】（1）‎2m/s2 （2）‎‎2.25m ‎【解析】‎ ‎【详解】（1）撤去推力后冰壶减速运动加速度为a2, ‎ μmg=ma2‎ 解得：a2=‎2m/s2‎ ‎（2）冰壶刚好滑到C点时推力作用的距离最长 由，解得xm=‎2.25m．‎ 答：（1）‎2m/s2 （2）‎‎2.25m ‎16. 如图所示，质量M＝2kg的木块套在水平杆上，并用轻绳与质量m＝kg的小球相连，今用跟水平方向成α＝30°角的力F＝10N拉着球带动木块一起向右匀速运动，运动中M、m相对位置保持不变，g取10N/kg，求：‎ ‎（1）运动过程中轻绳与水平方向夹角θ；‎ ‎（2）木块与水平杆间的动摩擦因数μ。‎ ‎【答案】（1）30°；（2）0.35‎ ‎【解析】‎ ‎【详解】（1）以球为研究对象，受力分析，据共点力平衡条件得 Fcos30°－FTcosθ＝0‎ Fsin30°＋FTsinθ＝mg 解得 FT＝10N θ＝30°‎ ‎（2）以木块M为研究对象，其受力如图所示 据共点力平衡条件得 FTcos30°－Ff＝0‎ FN－Mg－FTsin30°＝0‎ Ff＝μFN 解得 μ＝0.35‎ ‎17. 一在隧道中行驶的汽车A以的速度向东做匀速直线运动，发现前方相距处、以的速度同向运动的汽车B正开始匀减速刹车，其刹车的加速度大小 ‎,从此刻开始计时，若汽车A不采取刹车措施，汽车B刹车直到静止后保持不动，求：‎ ‎（1）汽车A追上汽车B前，A、B两汽车间的最远距离；‎ ‎（2）汽车A恰好追上汽车B需要的时间．‎ ‎【答案】（1）‎16m（2）8s ‎【解析】‎ ‎(1)当A、B两汽车速度相等时，两车间的距离最远，即 v＝vB－at＝vA 得t＝＝3 s 此时汽车A的位移xA＝vAt＝‎12 m ；‎ 汽车B的位移xB＝vBt－at2＝‎‎21 m A、B两汽车间的最远距离Δxm＝xB＋x0－xA＝‎‎16 m ‎(2)汽车B从开始减速直到静止经历的时间t1＝＝5 s ‎ 运动的位移x′B＝＝‎‎25 m 汽车A在t1时间内运动的位移 x′A＝vAt1＝‎20 m ‎ 此时相距Δx＝x′B＋x0－x′A＝‎‎12 m 汽车A需要再运动的时间t2＝＝3 s ‎ 故汽车A追上汽车B所用时间t＝t1＋t2＝8 s ‎18. 如图甲所示，质量m=‎1kg的物块在平行斜面向上的拉力F作用下从静止开始沿斜面向上运动，t=0.5s时撤去拉力，利用速度传感器得到其速度随时间的变化关系图象（v-t图象）如图乙所示，g取‎10m/s2，求：‎ ‎（1）2s内物块的位移大小x和通过的路程L。‎ ‎（2）拉力F的大小。‎ ‎【答案】（1）‎0.5m ，‎1.5m；（2）8N ‎【解析】‎ ‎【详解】（1）在2s内，由图乙 物块上升的最大距离 物块下滑的距离 所以位移大小 路程 ‎（2）由图乙知，所求两个阶段加速度的大小 设斜面倾角为θ，斜面对物块的摩擦力为，根据牛顿第二定律有，在内 在内 解得 ‎19. 如图所示，倾角 ，质量M=‎34kg的斜面体，始终停在粗糙水平地面上．质量=‎14kg，=‎2kg的物体A和B，通过跨过定滑轮的细线连接．若物体A以a=‎2.5m/s2的加速度沿斜面下滑，求此过程中地面对斜面体的摩擦力和支持力各是多大？‎ ‎【答案】，‎ ‎【解析】‎ ‎【详解】对整体受力分析，如图所示；‎ 在水平方向，根据牛顿第二定律可得：‎ 在竖直方向，根据牛顿第二定律可得：‎ 解得地面对斜面体的支持力：‎