【物理】2020届一轮复习人教版机械能守恒定律及其应用课时作业(1) 9页

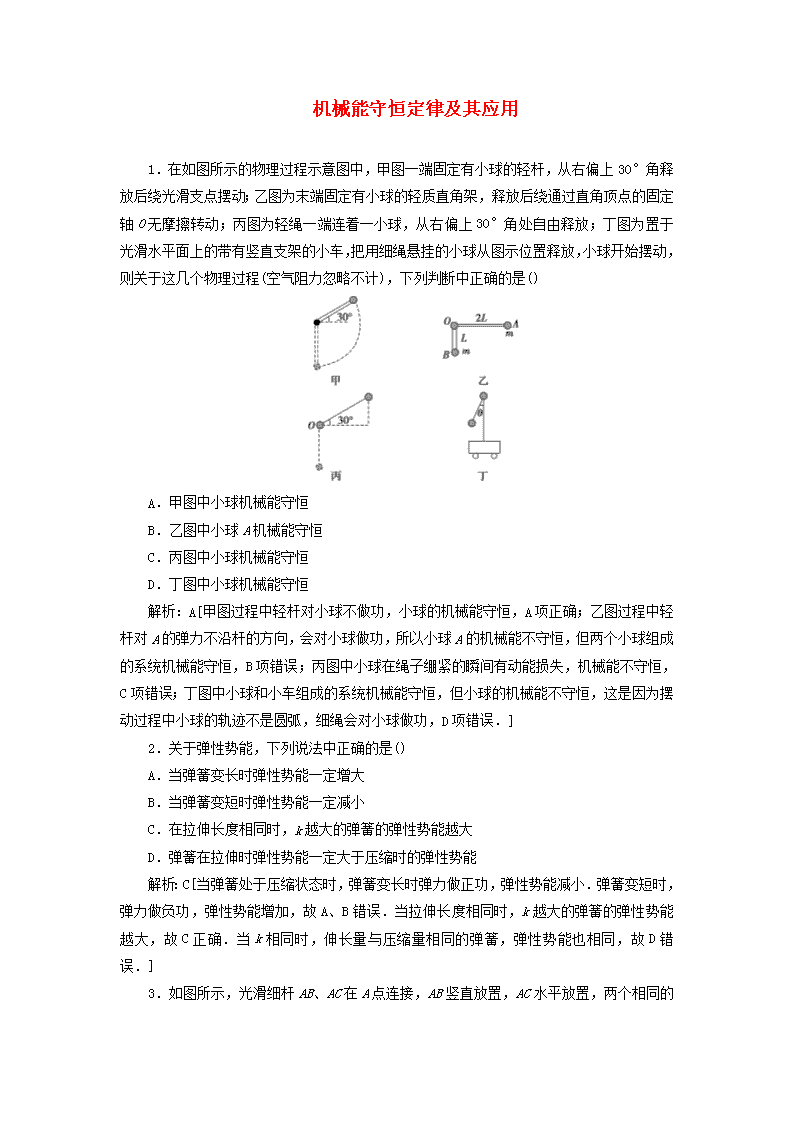
机械能守恒定律及其应用 ‎ ‎ ‎1．在如图所示的物理过程示意图中，甲图一端固定有小球的轻杆，从右偏上30°角释放后绕光滑支点摆动；乙图为末端固定有小球的轻质直角架，释放后绕通过直角顶点的固定轴O无摩擦转动；丙图为轻绳一端连着一小球，从右偏上30°角处自由释放；丁图为置于光滑水平面上的带有竖直支架的小车，把用细绳悬挂的小球从图示位置释放，小球开始摆动，则关于这几个物理过程(空气阻力忽略不计)，下列判断中正确的是()‎ A．甲图中小球机械能守恒 B．乙图中小球A机械能守恒 C．丙图中小球机械能守恒 D．丁图中小球机械能守恒 解析：A[甲图过程中轻杆对小球不做功，小球的机械能守恒，A项正确；乙图过程中轻杆对A的弹力不沿杆的方向，会对小球做功，所以小球A的机械能不守恒，但两个小球组成的系统机械能守恒，B项错误；丙图中小球在绳子绷紧的瞬间有动能损失，机械能不守恒，C项错误；丁图中小球和小车组成的系统机械能守恒，但小球的机械能不守恒，这是因为摆动过程中小球的轨迹不是圆弧，细绳会对小球做功，D项错误．]‎ ‎2．关于弹性势能，下列说法中正确的是()‎ A．当弹簧变长时弹性势能一定增大 B．当弹簧变短时弹性势能一定减小 C．在拉伸长度相同时，k越大的弹簧的弹性势能越大 D．弹簧在拉伸时弹性势能一定大于压缩时的弹性势能 解析：C[当弹簧处于压缩状态时，弹簧变长时弹力做正功，弹性势能减小．弹簧变短时，弹力做负功，弹性势能增加，故A、B错误．当拉伸长度相同时，k越大的弹簧的弹性势能越大，故C正确．当k相同时，伸长量与压缩量相同的弹簧，弹性势能也相同，故D错误．]‎ ‎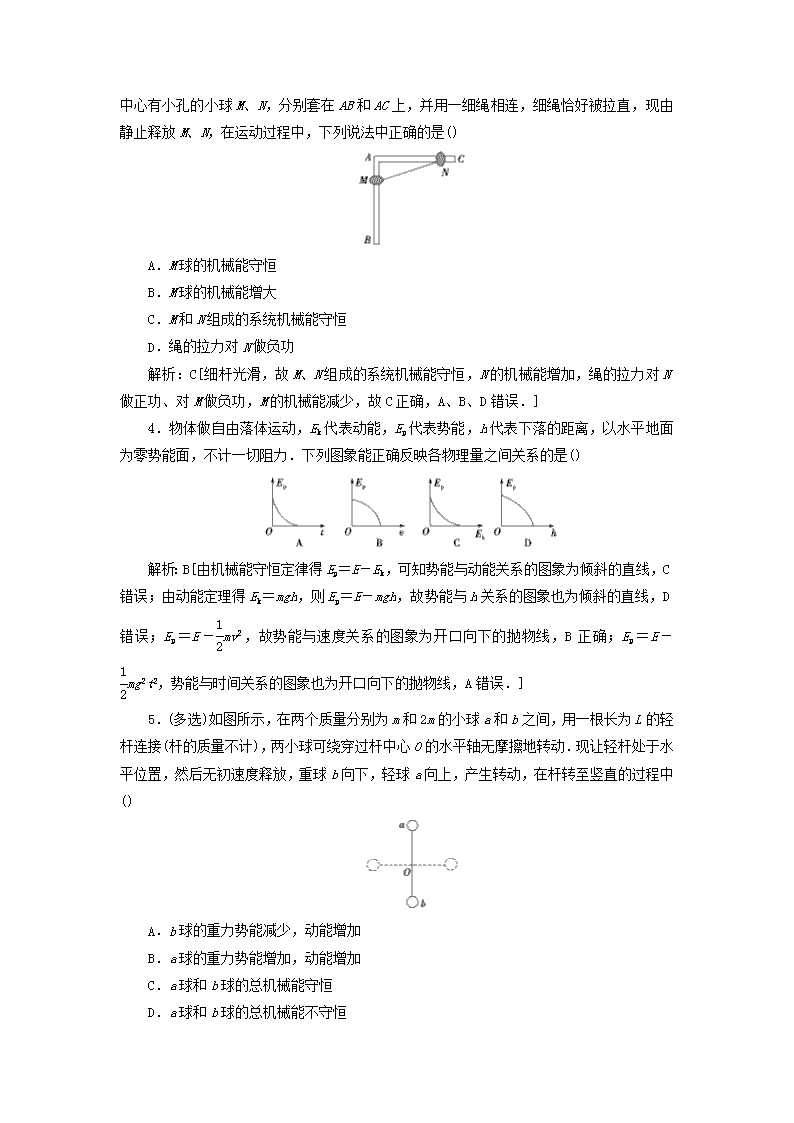3．如图所示，光滑细杆AB、AC在A点连接，AB竖直放置，AC 水平放置，两个相同的中心有小孔的小球M、N，分别套在AB和AC上，并用一细绳相连，细绳恰好被拉直，现由静止释放M、N，在运动过程中，下列说法中正确的是()‎ A．M球的机械能守恒 B．M球的机械能增大 C．M和N组成的系统机械能守恒 D．绳的拉力对N做负功 解析：C[细杆光滑，故M、N组成的系统机械能守恒，N的机械能增加，绳的拉力对N做正功、对M做负功，M的机械能减少，故C正确，A、B、D错误．]‎ ‎4．物体做自由落体运动，Ek代表动能，Ep代表势能，h代表下落的距离，以水平地面为零势能面，不计一切阻力．下列图象能正确反映各物理量之间关系的是()‎ 解析：B[由机械能守恒定律得Ep＝E－Ek，可知势能与动能关系的图象为倾斜的直线，C错误；由动能定理得Ek＝mgh，则Ep＝E－mgh，故势能与h关系的图象也为倾斜的直线，D错误；Ep＝E－mv2，故势能与速度关系的图象为开口向下的抛物线，B正确；Ep＝E－mg2t2，势能与时间关系的图象也为开口向下的抛物线，A错误．]‎ ‎5．(多选)如图所示，在两个质量分别为m和‎2m的小球a和b之间，用一根长为L的轻杆连接(杆的质量不计)，两小球可绕穿过杆中心O的水平轴无摩擦地转动．现让轻杆处于水平位置，然后无初速度释放，重球b向下，轻球a向上，产生转动，在杆转至竖直的过程中()‎ A．b球的重力势能减少，动能增加 B．a球的重力势能增加，动能增加 C．a球和b球的总机械能守恒 D．a球和b球的总机械能不守恒 解析：ABC[a、b 两球组成的系统中，只存在动能和重力势能的相互转化，系统的机械能守恒，选项C正确，D错误；其中a球的动能和重力势能均增加，机械能增加，轻杆对a球做正功；b球的重力势能减少，动能增加，总的机械能减少，轻杆对b球做负功，选项A、B正确．]‎ ‎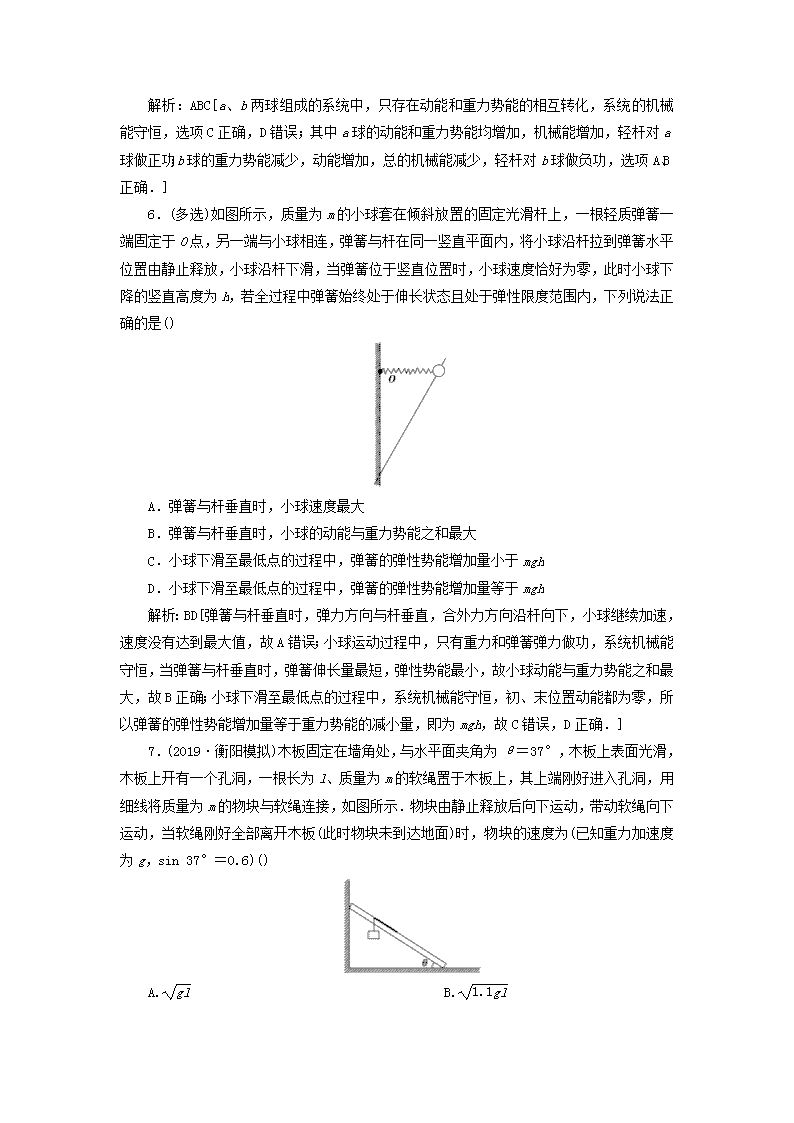6．(多选)如图所示，质量为m的小球套在倾斜放置的固定光滑杆上，一根轻质弹簧一端固定于O点，另一端与小球相连，弹簧与杆在同一竖直平面内，将小球沿杆拉到弹簧水平位置由静止释放，小球沿杆下滑，当弹簧位于竖直位置时，小球速度恰好为零，此时小球下降的竖直高度为h，若全过程中弹簧始终处于伸长状态且处于弹性限度范围内，下列说法正确的是()‎ A．弹簧与杆垂直时，小球速度最大 B．弹簧与杆垂直时，小球的动能与重力势能之和最大 C．小球下滑至最低点的过程中，弹簧的弹性势能增加量小于mgh D．小球下滑至最低点的过程中，弹簧的弹性势能增加量等于mgh 解析：BD[弹簧与杆垂直时，弹力方向与杆垂直，合外力方向沿杆向下，小球继续加速，速度没有达到最大值，故A错误；小球运动过程中，只有重力和弹簧弹力做功，系统机械能守恒，当弹簧与杆垂直时，弹簧伸长量最短，弹性势能最小，故小球动能与重力势能之和最大，故B正确；小球下滑至最低点的过程中，系统机械能守恒，初、末位置动能都为零，所以弹簧的弹性势能增加量等于重力势能的减小量，即为mgh，故C错误，D正确．]‎ ‎7．(2019·衡阳模拟)木板固定在墙角处，与水平面夹角为θ＝37°，木板上表面光滑，木板上开有一个孔洞，一根长为l、质量为m的软绳置于木板上，其上端刚好进入孔洞，用细线将质量为m的物块与软绳连接，如图所示．物块由静止释放后向下运动，带动软绳向下运动，当软绳刚好全部离开木板(此时物块未到达地面)时，物块的速度为(已知重力加速度为g，sin 37°＝0.6)()‎ A. B. C. D. 解析：C[在下落过程中，由几何关系可知，重物的重心下降高度为l；而软绳重心的下降高度为：‎ h′＝‎0.5l－0.5lsin 37°＝‎0.2l，‎ 故全过程中重力势能的减小量为：‎ ΔEp＝mgl＋0.2mgl＝1.2mgl；‎ 根据机械能守恒定律可得：·2mv2＝ΔEp 解得：v＝.]‎ ‎8.(2019·山东潍坊中学一模)如图所示，在竖直面内固定一光滑的硬质杆ab，杆与水平面的夹角为θ，在杆的上端a处套一质量为m的圆环，圆环上系一轻弹簧，弹簧的另一端固定在与a处在同一水平线上的O点，O、b两点处在同一竖直线上．由静止释放圆环后，圆环沿杆从a运动到b，在圆环运动的整个过程中，弹簧一直处于伸长状态，则下列说法正确的是()‎ A．圆环的机械能保持不变 B．弹簧对圆环一直做负功 C．弹簧的弹性势能逐渐增大 D．圆环和弹簧组成的系统机械能守恒 解析：D[由几何关系可知，当环与O点的连线与杆垂直时，弹簧的长度最短，弹簧的弹性势能最小，如图，所以在环从a到C的过程中弹簧对环做正功，弹簧的弹性势能减小，环的机械能增大，而从C到b的过程中，弹簧对环做负功，弹簧的弹性势能增大，环的机械能减小，故A、B、C错误；在整个过程中只有圆环的重力和弹簧的弹力做功，所以圆环和弹簧组成的系统机械能守恒，故D正确．]‎ ‎9．如图所示光滑轨道由半圆和一段竖直轨道构成，图中H＝2R，其中R远大于轨道内径．比轨道内径略小的两小球A、B用轻绳连接，A在外力作用下静止于轨道右端口，B球静止在地面上，轻绳绷紧．现静止释放A小球，A落地后不反弹，此后B小球恰好可以到达轨道最高点．则A、B两小球的质量之比为()‎ A．3∶1 B．3∶2‎ C．7∶1 D．7∶2‎ 解析：A[设A球落地时两球速度大小为v1.对于两球组成的系统，由机械能守恒定律得：A下落过程，有 mAgH＝mBgH＋(mA＋mB)v A落地后，对B球，由机械能守恒得：‎ B球上升过程，有mBv＝mBgR 又H＝2R 联立解得mA∶mB＝3∶1.故选A.]‎ ‎10．(多选)一蹦极运动员身系弹性蹦极绳从水面上方的高台下落，到最低点(在水面上方)时距水面还有数米距离．假定空气阻力可忽略不计，运动员可视为质点，下列说法正确的是()‎ A．运动员到达最低点前重力势能始终减小 B．蹦极绳张紧后的下落过程中，弹力做负功，弹性势能增加 C．蹦极过程中，运动员、地球和蹦极绳所组成的系统机械能守恒 D．蹦极过程中，运动员的重力势能的改变量与重力势能零点的选取有关 解析：ABC[运动员下落到最低点前，重力做正功，重力势能减小，A正确；蹦极绳张紧后的下落过程中，弹力做负功，弹性势能增加，B正确；蹦极过程中，对运动员、地球和蹦极绳所组成的系统，除重力和弹力外其他力不做功，系统机械能守恒，C正确；蹦极过程中，运动员的重力势能的大小与重力势能零点的选择有关，但运动员的重力势能的改变量与重力势能零点的选择无关，D错误．]‎ ‎[B级—能力练]‎ ‎11．(2019·云南模拟)(多选)如图所示，一质量为m的小球套在光滑竖直杆上，轻质弹簧一端与小球相连，另一端固定于O点．现将小球从A点由静止释放，沿竖直杆运动到B点，已知OA长度小于OB长度，弹簧处于OA、OB两位置时弹力大小相等，A、B两点间的距离为h.在小球由A到B的过程中，下列说法正确的是()‎ A．弹簧处于OA、OB两位置时的弹性势能不相等 B．小球在B点时的动能为mgh C．小球的加速度等于重力加速度g的位置只有一个 D．在弹簧与杆垂直时，小球机械能最小 解析：BD[现将小球从A点由静止释放，沿竖直杆运动到B点，在小球由A到B的过程中，由于弹簧处于OA、OB两位置时弹力大小相等，根据胡克定律可知弹簧形变量相等，根据同一轻弹簧的弹性势能只与形变量有关，所以弹簧处于OA、OB两位置时的弹性势能相等，A项错误．在小球由A到B的过程中，由机械能守恒定律，小球在B点时的动能为Ek＝mgh，B项正确．在小球由A到B的过程中，在小球下落到与O点在同一水平位置时，即在弹簧与杆垂直时，在竖直方向只受重力作用，加速度为重力加速度g；在小球下落到轻弹簧恢复到原长时，在竖直方向只受重力作用，加速度为重力加速度g；所以在小球由A到B的过程中，小球的加速度等于重力加速度g的位置有两个，C项错误．在小球由A点下落到与O点在同一水平位置的过程中，轻弹簧的弹力对小球做负功，小球的机械能减小；在小球由与O点在同一水平位置继续下落的过程中，轻弹簧的弹力对小球做正功，小球的机械能增大，所以在弹簧与杆垂直时，小球机械能最小，D项正确．]‎ ‎12．如图所示，位于竖直平面上有圆弧的光滑轨道，半径为R，OB沿竖直方向，圆弧轨道上端A点距地面高度为H.当把质量为m的钢球从A点静止释放，最后落在了水平地面上的C点处．若本地的重力加速度为g，且不计空气阻力．求：‎ ‎(1)钢球运动到B点的瞬间受到的支持力多大．‎ ‎(2)钢球落地点C距B点的水平距离s为多少．‎ ‎(3)比值为多少时，小球落地点C距B点的水平距离s最大？这个最大值是多少？‎ 解析：(1)钢球由A到B过程由机械能守恒定律得：‎ mgR＝mv2‎ 在B点对钢球由牛顿第二定律得：‎ FN－mg＝m 解得：FN＝3mg ‎(2)钢球离开B点后做平抛运动，则有：‎ H－R＝gt2‎ s＝vt 解得：s＝2 ‎(3)s＝2 ＝2 根据数学知识可知，当R＝H，即＝时，s有最大值，s最大＝H.‎ 答案：(1)3mg(2)2 (3)H ‎13．(2018·张掖模拟)如图所示，在同一竖直平面内，一轻质弹簧一端固定，另一自由端恰好与水平线AB平齐，静止放于倾角为53°的光滑斜面上，一长为L＝‎0.45 m的轻质细绳一端固定在O点，另一端系一质量为m＝‎1 kg的小球，将细绳拉至水平，使小球在位置C由静止释放，小球到达最低点D时，细绳刚好被拉断，之后小球在运动过程中恰好沿斜面方向切入并将弹簧压缩，最大压缩量为x＝‎5 cm(g取‎10 m/s2，sin 53°＝0.8，cos 53°＝0.6)，求：‎ ‎(1)小球运动到D点的速度．‎ ‎(2)小球运动到斜面顶端A点时的速度．‎ ‎(3)弹簧所获得的最大弹性势能Ep.‎ 解析：(1)小球由C到D，由机械能守恒定律得：‎ mgL＝mv 解得：vD＝＝ m/s＝‎3 m/s ‎(2)从D点小球开始做平抛运动，到A点时，根据矢量的分解可得：cos 53°＝ 解得：vA＝‎5 m/s ‎(3)小球从C点到将弹簧压缩至最短的过程中，小球与弹簧系统的机械能守恒，则：‎ Ep＝mgxsin 53°＋mv＝12.9 J.‎ 答案：(1)‎3 m/s(2)‎5 m/s(3)12.9 J ‎14．(2019·辛集市统考)如图所示，竖直光滑的固定杆上套有一滑块A，滑块通过细绳绕过光滑滑轮连接物块B，B又通过一轻质弹簧连接物块C，C静止在地面上．开始用手托住A，使绳子刚好伸直处于水平位置但无张力，现将A由静止释放，当A、B速度达到最大时，C也刚好同时离开地面(此时B还没有到达滑轮位置)．已知：mA＝‎1.2 kg，mB＝mC＝‎1.0 kg，滑轮与杆的水平距离L＝‎0.8 m，g取‎10 m/s2.试求：‎ ‎(1)A下降多大距离时速度最大？‎ ‎(2)弹簧的劲度系数k；‎ ‎(3)A的最大速度是多少？‎ 解析：(1)如图所示，设A下降h时速度达最大，此时绳与杆夹角为θ，‎ 绳中张力为T.因为A物块速度达到最大，故加速度为零，即受力平衡，‎ 有mAg＝Tcos θ，‎ 此时C刚好离开地面，故T＝(mB＋mC)g＝20 N，‎ 解得cos θ＝0.6，即θ＝53°，‎ 所以h＝＝ m＝‎0.6 m.‎ ‎(2)开始时绳中无张力，对B分析，有mBg＝kx1，‎ C离开地面时，有mCg＝kx2，‎ 又x1＋x2＝－L 可解得k＝100 N/m.‎ ‎(3)由(2)知，x1＝x2＝‎0.1 m，故初、末状态弹簧的弹性势能相等，对A、B、C及弹簧系统由机械能守恒定律有 mAgh－mBg(x1＋x2)＝mAv＋mBv 又vB＝vAcos θ 联立可解得vA＝ m/s.‎ 答案：(1)‎0.6 m(2)100 N/m(3) m/s