【物理】2018届二轮复习动量守恒定律典型计算题学案（全国通用） 4页

动量守恒定律 例题1．如图所示，质量均为m的小车和木箱紧挨着静止在光滑的水平冰面上，质量为‎2m的小孩站在小车上用力向右迅速推出木箱，木箱相对于冰面运动的速度为v，木箱运动到右侧墙壁时与竖直墙壁发生弹性碰撞，反弹后能被小孩接住，求：‎ ‎(1)小孩接住箱子后共同速度的大小；‎ ‎(2)若小孩接住箱子后再次以相对于冰面的速度v将木箱向右推出，木箱仍与竖直墙壁发生弹性碰撞，判断小孩能否再次接住木箱．‎ 解析：(1)取向左为正方向，根据动量守恒定律可得 推出木箱的过程中0＝(m＋‎2m)v1－mv，‎ 接住木箱的过程中mv＋(m＋‎2m)v1＝(m＋m＋‎2m)v2.‎ 解得v2＝.‎ ‎(2)若小孩第二次将木箱推出，根据动量守恒定律可得 ‎4mv2＝3mv3－mv，‎ 则v3＝v，‎ 故无法再次接住木箱．‎ 答案：(1)　(2)否 例题2．如图所示，光滑水平轨道上放置长板A(上表面粗糙)和滑块C，滑块B置于A的左端．三者质量分别为mA＝‎2 kg、mB＝‎1 kg、mC＝‎2 kg，开始时C静止，A、B一起以v0＝‎5 m/s的速度匀速向右运动，A与C相碰撞(时间极短)后C向右运动，经过一段时间，A、B再次达到共同速度一起向右运动，且恰好不再与C碰撞．求A与C发生碰撞后瞬间A的速度大小．‎ 解析：因碰撞时间极短，A与C碰撞过程动量守恒，设碰撞后瞬间A的速度大小为vA，C的速度大小为vC，‎ 以向右为正方向，由动量守恒定律得mAv0＝mAvA＋mCvC，A与B在摩擦力作用下达到共同速度，设共同速度为vAB，‎ 由动量守恒定律得mAvA＋mBv0＝(mA＋mB)vAB，‎ A、B达到共同速度后恰好不再与C碰撞，应满足vAB＝vC，联立解得vA＝‎2 m/s.‎ 答案：‎2 m/s 例题3．人和冰车的总质量为M，另一木球质量为m，且M∶m＝31∶‎ ‎2.人坐在静止于水平冰面的冰车上，以速度v(相对地面)将原来静止的木球沿冰面推向正前方向的固定挡板，不计一切摩擦阻力，设小球与挡板的碰撞是弹性的，人接住球后，再以同样的速度v(相对地面)将球推向挡板．求人推多少次后不能再接到球？‎ 解析：设第1次推球后人的速度为v1，有0＝Mv1－mv，‎ 第1次接球后人的速度为v1′，有Mv1＋mv＝(M＋m)v1′；‎ 第2次推球(M＋m)v1′＝Mv2－mv，‎ 第2次接球Mv2＋mv＝(M＋m)v2′……‎ 第n次推球 ‎(M＋m)vn－1′＝Mvn－mv，‎ 可得vn＝，‎ 当vn≥v时人便接不到球，可得n≥8.25，取n＝9.‎ 答案：9次 例题4．如图所示，甲、乙两名宇航员正在离空间站一定距离的地方执行太空维修任务．某时刻甲、乙都以大小为v0＝‎2 m/s的速度相向运动，甲、乙和空间站在同一直线上且可当成质点．甲和他的装备总质量为M1＝‎90 kg，乙和他的装备总质量为M2＝‎135 kg，为了避免直接相撞，乙从自己的装备中取出一质量为m＝‎45 kg的物体A推向甲，甲迅速接住A后即不再松开，此后甲、乙两宇航员在空间站外做相对距离不变的同向运动，且安全“飘”向空间站．(设甲、乙距离空间站足够远，本题中的速度均指相对空间站的速度)‎ ‎(1)乙要以多大的速度v(相对于空间站)将物体A推出？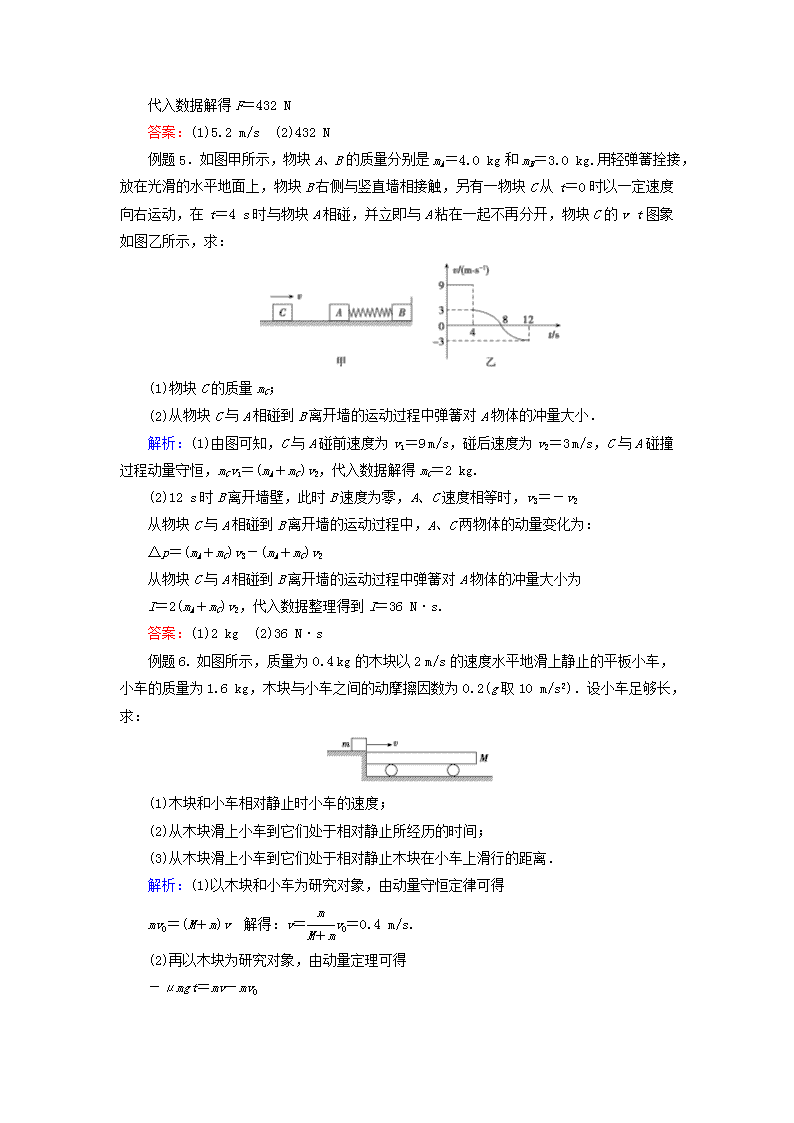‎ ‎(2)设甲与物体A作用时间为t＝0.5 s，求甲与A的相互作用力F的大小．‎ 解析：(1)以甲、乙、A三者组成的系统为研究对象，系统动量守恒，以乙的方向为正方向，‎ 则有：M2v0－M1v0＝(M1＋M2)v1‎ 以乙和A组成的系统为研究对象，有：‎ M2v0＝(M2－m)v1＋mv 代入数据联立解得 v1＝‎0.4 m/s，v＝‎5.2 m/s ‎(2)以甲为研究对象，由动量定理得，‎ Ft＝M1v1－(－M1v0)‎ 代入数据解得F＝432 N 答案：(1)‎5.2 m/s　(2)432 N 例题5．如图甲所示，物块A、B的质量分别是mA＝‎4.0 kg和mB＝‎3.0 kg.用轻弹簧拴接，放在光滑的水平地面上，物块B右侧与竖直墙相接触，另有一物块C从t＝0时以一定速度向右运动，在t＝4 s时与物块A相碰，并立即与A粘在一起不再分开，物块C的vt图象如图乙所示，求：‎ ‎(1)物块C的质量mC；‎ ‎(2)从物块C与A相碰到B离开墙的运动过程中弹簧对A物体的冲量大小．‎ 解析：(1)由图可知，C与A碰前速度为v1＝‎9 m/s，碰后速度为v2＝‎3 m/s，C与A碰撞过程动量守恒，mCv1＝(mA＋mC)v2，代入数据解得mC＝‎2 kg.‎ ‎(2)12 s时B离开墙壁，此时B速度为零，A、C速度相等时，v3＝－v2‎ 从物块C与A相碰到B离开墙的运动过程中，A、C两物体的动量变化为：‎ Δp＝(mA＋mC)v3－(mA＋mC)v2‎ 从物块C与A相碰到B离开墙的运动过程中弹簧对A物体的冲量大小为 I＝2(mA＋mC)v2，代入数据整理得到I＝36 N·s.‎ 答案：(1)‎2 kg　(2)36 N·s 例题6. 如图所示，质量为‎0.4 kg的木块以‎2 m/s的速度水平地滑上静止的平板小车，小车的质量为‎1.6 kg，木块与小车之间的动摩擦因数为0.2(g取‎10 m/s2)．设小车足够长，求：‎ ‎(1)木块和小车相对静止时小车的速度；‎ ‎(2)从木块滑上小车到它们处于相对静止所经历的时间；‎ ‎(3)从木块滑上小车到它们处于相对静止木块在小车上滑行的距离．‎ 解析：(1)以木块和小车为研究对象，由动量守恒定律可得 mv0＝(M＋m)v　解得：v＝v0＝‎0.4 m/s.‎ ‎(2)再以木块为研究对象，由动量定理可得 ‎－μmgt＝mv－mv0‎ 解得：t＝＝0.8 s.‎ ‎(3)木块做匀减速运动，加速度为 a1＝＝μg＝‎2 m/s2‎ 小车做匀加速运动，加速度为 a2＝＝＝‎0.5 m/s2‎ 在此过程中木块的位移为 x1＝＝‎‎0.96 m 小车的位移为：x2＝a2t2＝×0.5×‎0.82 m＝‎‎0.16 m 由此可知，木块在小车上滑行的距离为：‎ Δx＝x1－x2＝‎0.8 m.‎ 答案：(1)‎0.4 m/s　(2)0.8 s　(3)0.8 m