2018届高考物理第一轮总复习全程训练课练16机械能守恒定律及应用 19页

课练16　机械能守恒定律及应用 ‎1.如图，两根相同的轻质弹簧，沿足够长的光滑斜面放置，下端固定在斜面底部挡板上，斜面固定不动．质量不同、形状相同的两物块 分别置于两弹簧上端．现用外力作用在物块上，使两弹簧具有相同的压缩量，若撤去外力后，两物块由静止沿斜面向上弹出并离开弹簧，则从撤去外力到物块速度第一次减为零的过程，两物块(　　)‎ A．最大速度相同 B．最大加速度相同 C．上升的最大高度不同 D．重力势能的变化量不同 ‎2．(多选)‎ 如图所示，楔形木块abc固定在水平面上，粗糙斜面ab和光滑斜面bc与水平面的夹角相同，顶角b处安装一定滑轮．质量分别为M、m(M＞m)的滑块，通过不可伸长的轻绳跨过定滑轮连接，轻绳与斜面平行．两滑块由静止释放后，沿斜面做匀加速运动．若不计滑轮的质量和摩擦，在两滑块沿斜面运动的过程中(　　)‎ A．两滑块组成系统的机械能守恒 B．重力对M做的功等于M动能的增加 C．轻绳对m做的功等于m机械能的增加 D．两滑块组成系统的机械能损失等于M克服摩擦力做的功 ‎3.‎ ‎(多选)质量为m的小球从桌面以速度v竖直向上抛出，桌面离地高度为h，小球能达到的最大离地高度为H.若以桌面作为参考平面，不计空气阻力，则(　　)‎ A．小球抛出时的机械能为mgh＋mv2‎ B．小球在最高点的机械能为mgH C．小球在最高点的机械能为mg(H－h)‎ D．小球落地前瞬间的机械能为mv2‎ ‎4.‎ ‎(多选)半径为r和R(rva>vb D．va>vb>vc ‎6.‎ 如图所示小球沿水平面通过O点进入半径为R的光滑半圆弧轨道后恰能通过最高点P，然后落回水平面．不计空气阻力．下列说法不正确的是(　　)‎ A．小球落地点离O点的水平距离为2R B．小球落地时的动能为 C．小球运动到半圆弧最高点P时向心力为零 D．若将半圆弧轨道上部的圆弧截去，其他条件不变，则小球能达到的最大高度比P点高0.5R ‎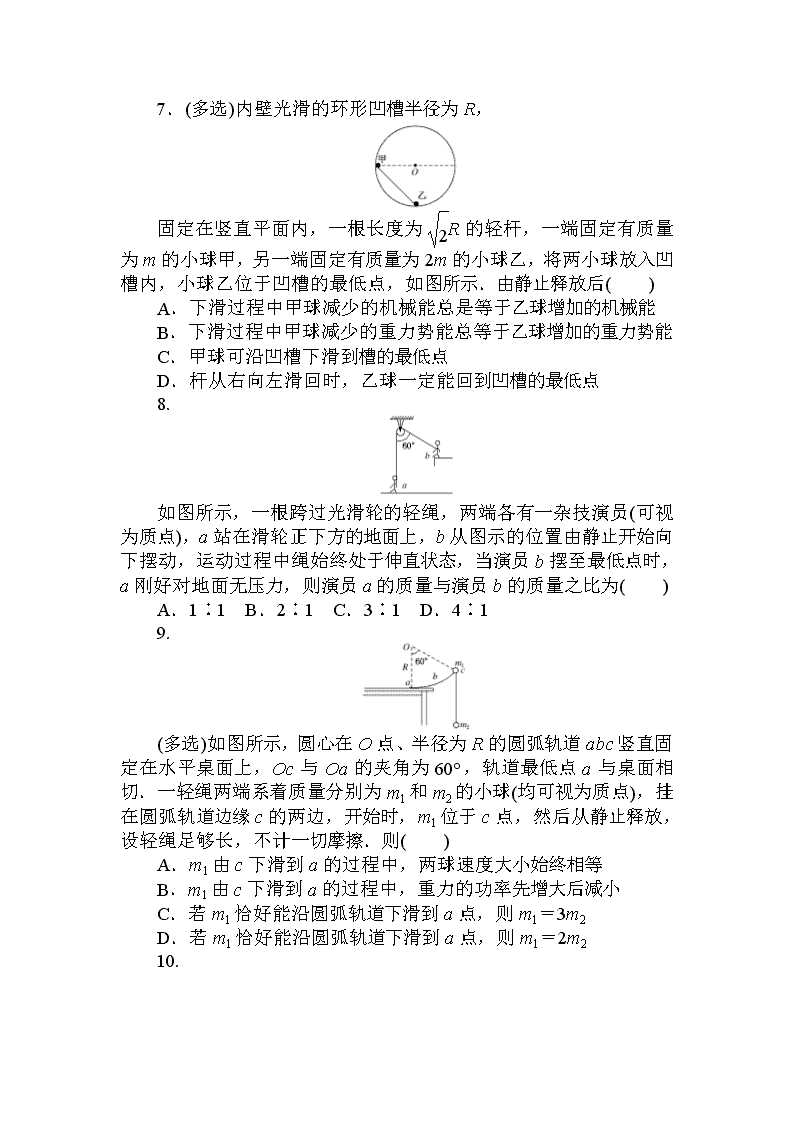7．(多选)内壁光滑的环形凹槽半径为R，‎ 固定在竖直平面内，一根长度为R的轻杆，一端固定有质量为m的小球甲，另一端固定有质量为2m的小球乙，将两小球放入凹槽内，小球乙位于凹槽的最低点，如图所示．由静止释放后(　　)‎ A．下滑过程中甲球减少的机械能总是等于乙球增加的机械能 B．下滑过程中甲球减少的重力势能总等于乙球增加的重力势能 C．甲球可沿凹槽下滑到槽的最低点 D．杆从右向左滑回时，乙球一定能回到凹槽的最低点 ‎8.‎ 如图所示，一根跨过光滑轮的轻绳，两端各有一杂技演员(可视为质点)，a站在滑轮正下方的地面上，b从图示的位置由静止开始向下摆动，运动过程中绳始终处于伸直状态，当演员b摆至最低点时，a刚好对地面无压力，则演员a的质量与演员b的质量之比为(　　)‎ A．1∶1 B．2∶1 C．3∶1 D．4∶1‎ ‎9.‎ ‎(多选)如图所示，圆心在O点、半径为R的圆弧轨道abc竖直固定在水平桌面上，Oc与Oa的夹角为60°，轨道最低点a与桌面相切．一轻绳两端系着质量分别为m1和m2的小球(均可视为质点)，挂在圆弧轨道边缘c的两边，开始时，m1位于c点，然后从静止释放，设轻绳足够长，不计一切摩擦．则(　　)‎ A．m1由c下滑到a的过程中，两球速度大小始终相等 B．m1由c下滑到a的过程中，重力的功率先增大后减小 C．若m1恰好能沿圆弧轨道下滑到a点，则m1＝3m2‎ D．若m1恰好能沿圆弧轨道下滑到a点，则m1＝2m2‎ ‎10.‎ 如图所示，一劲度系数为k 的轻质弹簧下端固定在水平面上，上端叠放着两个质量均为M的物块A、B，B与弹簧拴接，初始时系统处于静止状态．现用竖直向上的力F拉A，使A开始向上做加速度为a的匀加速运动，测得两个物块的速度—时间图象如图乙所示，重力加速度g已知，则(　　)‎ A．施加外力的瞬间，A、B间的弹力大小为M(g－a)‎ B．A、B在t1时刻分离，此时弹簧弹力恰好为零 C．弹簧恢复到原长时，B的速度达到最大值 D．在0～t2时间内，B与弹簧组成的系统的机械能先逐渐增加，后保持不变 ‎11.‎ 如图所示，质量为m的小球从四分之一光滑圆弧轨道顶端静止释放，从轨道末端O点水平抛出，击中平台右下侧挡板上的P点．以O为原点在竖直面内建立如图所示的平面直角坐标系，挡板形状满足方程y＝6－x2(单位：m)，小球质量m＝0.4 kg，圆弧轨道半径R＝1.25 m，g取10 m/s2，求：‎ ‎(1)小球对圆弧轨道末端的压力大小．‎ ‎(2)小球从O点到P点所需的时间(结果可保留根号)．‎ ‎12.‎ 如图所示，一内壁光滑的细管弯成半径为R＝0.4 m的半圆形轨道CD，竖直放置，其内径略大于小球的直径，水平轨道与竖直半圆轨道在C点连接完好．置于水平轨道上的弹簧左端与竖直墙壁相连，B处为弹簧的自然状态．将一个质量为m＝0.8 kg的小球放在弹簧的右侧后，用力向左侧推小球而压缩弹簧至A 处，然后将小球由静止释放，小球运动到C处后对轨道的压力为F1＝58 N．水平轨道以B处为界，左侧AB段长为x＝0.3 m，与小球的动摩擦因数为μ＝0.5，右侧BC段光滑．g取10 m/s2，求：‎ ‎(1)弹簧在压缩时所储存的弹性势能．‎ ‎(2)小球运动到轨道最高处D点时对轨道的压力大小．‎ ‎　 　 　　 　　　　　　　　　　　　　　　　　　　　‎ ‎1．(2016·课标Ⅱ)小球P和Q用不可伸长的轻绳悬挂在天花板上，P球的质量大于Q球的质量，悬挂P球的绳比悬挂Q球的绳短．将两球拉起，使两绳均被水平拉直，如图所示．将两球由静止释放．在各自轨迹的最低点，(　　)‎ A．P球的速度一定大于Q球的速度 B．P球的动能一定小于Q球的动能 C．P球所受绳的拉力一定大于Q球所受绳的拉力 D．P球的向心加速度一定小于Q球的向心加速度 ‎2．(多选)‎ ‎(2016·浙江理综)如图所示为一滑草场．某条滑道由上下两段高均为h，与水平面倾角分别为45°和37°的滑道组成，滑草车与草地之间的动摩擦因数为μ.质量为m的载人滑草车从坡顶由静止开始自由下滑，经过上、下两段滑道后，最后恰好静止于滑道的底端(不计滑草车在两段滑道交接处的能量损失，sin37°＝0.6，cos37°＝0.8)．则(　　)‎ A．动摩擦因数μ＝ B．载人滑草车最大速度为 C．载人滑草车克服摩擦力做功为mgh D．载人滑草车在下段滑道上的加速度大小为g ‎3．(2015·北京理综)“蹦极”运动中，长弹性绳的一端固定，另一端绑在人身上，人从几十米高处跳下．将蹦极过程简化为人沿竖直方向的运动．从绳恰好伸直，到人第一次下降至最低点的过程中，下列分析正确的是(　　)‎ A．绳对人的冲量始终向上，人的动量先增大后减小 B．绳对人的拉力始终做负功，人的动能一直减小 C．绳恰好伸直时，绳的弹性势能为零，人的动能最大 D．人在最低点时，绳对人的拉力等于人所受的重力 ‎4.‎ ‎(2016·课标Ⅱ)轻质弹簧原长为2l，将弹簧竖直放置在地面上，在其顶端将一质量为5m的物体由静止释放，当弹簧被压缩到最短时，弹簧长度为l.现将该弹簧水平放置，一端固定在A点，另一端与物块P接触但不连接．AB是长度为5l的水平轨道，B端与半径为l的光滑半圆轨道BCD相切，半圆的直径BD竖直，如图所示．物块P与AB间的动摩擦因数μ＝0.5.用外力推动物块P，将弹簧压缩至长度l，然后放开，P开始沿轨道运动．重力加速度大小为g.‎ ‎(1)若P的质量为m，求P到达B点时速度的大小，以及它离开圆轨道后落回到AB上的位置与B点之间的距离；‎ ‎(2)若P能滑上圆轨道，且仍能沿圆轨道滑下，求P的质量的取值范围．‎ ‎5.‎ ‎(2017·山西右玉一模)一小球以一定的初速度从图示位置进入光滑的轨道，小球先进入圆轨道1，再进入圆轨道2，圆轨道1的半径为R，圆轨道2的半径是轨道1的1.8倍，小球的质量为m ‎，若小球恰好能通过轨道2的最高点B，则小球在轨道1上经过A处时对轨道的压力为(　　)‎ A．2mg B．3mg C．4mg D．5mg ‎6.‎ ‎(2017·安徽第三次联考)如图所示，光滑轨道由AB、BCDE两段细圆管平滑连接组成，其中AB段水平，BCDE段为半径为R的四分之三圆弧，圆心O及D点与AB等高，整个轨道固定在竖直平面内，现有一质量为m，初速度v0＝的光滑小球水平进入圆管AB，设小球经过轨道交接处无能量损失，圆管孔径远小于R，则(小球直径略小于管内径)(　　)‎ A．小球到达C点时的速度大小vC＝ B．小球能通过E点且抛出后恰好落至B点 C．无论小球的初速度v0为多少，小球到达E点时的速度都不能为零 D．若将DE轨道拆除，则小球能上升的最大高度与D点相距2R ‎7.‎ ‎(多选)(2017·陕西商洛模拟)如图所示，将质量为2m的重物悬挂在轻绳的一端，轻绳的另一端系一质量为m的小环，小环套在竖直固定的光滑直杆上，光滑定滑轮与直杆的距离为d.杆上的A点与定滑轮等高，杆上的B点在A点正下方距离为d处．现将环从A处由静止释放，不计一切摩擦阻力，下列说法正确的是(　　)‎ A．环到达B处时，重物上升的高度h＝ B．环到达B处时，环与重物的速度大小相等 C．环从A到B，环减少的机械能等于重物增加的机械能 D．环能下降的最大高度为d ‎8.‎ ‎(2017·山西太原二模)如图，轻弹簧的劲度系数为k，上端与一质量为m的木块A相连，下端与另一质量也为m的木块B相连，整个系统置于水平面上并处于静止状态．现用竖直向上的恒力F拉木块A使之向上运动，当B刚要离开地面时，A的速度为v.则(　　)‎ A．F刚作用于A时，A的加速度大小为 B．从F作用于A到B刚要离开地面的过程中，A上升的高度为 C．当B刚要离开地面时，A的加速度大小为－g D．当B刚要离开地面时，弹簧对B做功的瞬时功率为Fv ‎9.‎ ‎(2017·湖北黄冈模拟)如图所示，长1 m的轻杆BO一端通过光滑铰链铰在竖直墙上，另一端装一轻小光滑滑轮，绕过滑轮的细线一端悬挂重为15 N的物体G，另一端A系于墙上，平衡时OA恰好水平，现将细线A端沿着竖直墙向上缓慢移动一小段距离，同时调整轻杆与墙面夹角，系统重新平衡后轻杆受到的压力恰好也为15 N，则该过程中物体G增加的重力势能约为(　　)‎ A．1.3 J B．3.2 J C．4.4 J D．6.2 J ‎10.‎ ‎(多选)(2016·四川广元模拟)如图所示是一儿童游戏机的工作示意图，游戏机的光滑面板与水平面夹角为θ，半径为R的四分之一圆弧轨道BC与AB管道相切于B点，C 点为圆弧轨道最高点，轻弹簧下端固定在AB管道的底端，上端系一轻绳，轻绳通过弹簧内部连一手柄P.将弹珠投入AB管道内，缓慢下拉手柄使弹簧被压缩，释放手柄，弹珠被弹出，与游戏面板内的障碍物发生一系列碰撞后落入弹槽里，根据入槽情况可以获得不同的奖励．假设所有轨道均光滑，忽略空气阻力，弹珠可视为质点．某次缓慢下拉手柄，使弹珠距B点为L，释放手柄，弹珠被弹出，到达C点时速度为v，弹珠质量为m，重力加速度为g，下列说法正确的是(　　)‎ A．弹珠从释放手柄开始到触碰障碍物之前的过程中机械能守恒 B．此过程中，弹簧的最大弹性势能为mg(L＋R)sinθ＋mv2‎ C．弹珠脱离弹簧的瞬间，其动能与重力势能之和达到最大 D．调整手柄的位置使L变化，可以使弹珠从C点离开后做匀变速直线运动，直到碰到障碍物 ‎11．(2017·福建厦门质检)如图所示，在竖直方向上A、B两物体通过劲度系数为k的轻质弹簧相连，A放在水平地面上；B、C两物体通过细线绕过轻质定滑轮相连，C放在固定的光滑斜面上．用手拿住C，使细线刚刚拉直但无拉力作用，并保证ab段的细线竖直、cd段的细线与斜面平行．已知A、B的质量均为m，斜面倾角为θ＝37°，重力加速度为g，滑轮的质量和摩擦不计，开始时整个系统处于静止状态．C释放后沿斜面下滑，当A刚要离开地面时，B的速度最大，(sin37°＝0.6，cos37°＝0.8)求：‎ ‎(1)从开始到物体A刚要离开地面的过程中，物体C沿斜面下滑的距离；‎ ‎(2)C的质量；‎ ‎(3)A刚要离开地面时，C的动能．‎ ‎12．(2017·抚顺模拟)‎ 如图所示，将一质量为m＝0.1 kg的小球自水平平台右端 O点以初速度v0水平抛出，小球飞离平台后由A点沿切线方向落入竖直光滑圆轨道ABC，并沿轨道恰好通过最高点C，圆轨道ABC的形状为半径R＝2.5 m的圆截去了左上角127°的圆弧，CB为其竖直直径，(sin53°＝0.8，cos53°＝0.6，重力加速度g取10 m/s2)求：‎ ‎(1)小球经过C的速度大小．‎ ‎(2)小球运动到轨道最低点B时轨道对小球的支持力的大小．‎ ‎(3)平台末端O点到A点的竖直高度H.‎ 课练16　机械能守恒定律及应用 ‎1．C　物块受力平衡时具有最大速度，即mgsinθ＝kΔx，则质量大的物块具有最大速度时弹簧的压缩量比较大，上升的高度比较低，即位移小，而运动过程中质量大的物块平均加速度较小，v2－02＝2ax，加速度小的位移小，则最大速度v较小，故A错误；开始时物块具有最大加速度，开始弹簧形变量相同，则弹力相同，根据牛顿第二定律a＝，可见，质量大的最大加速度较小，故B错误；由题意使两弹簧具有相同的压缩量，则储存的弹性势能相等，物块上升到最大高度时，弹性势能完全转化为重力势能，则物块最终的重力势能相等，重力势能的变化量相等，而两物块质量不同，则上升的最大高度不同，故C正确、D错误．‎ ‎2．CD　由于斜面ab粗糙，滑块M运动过程中，摩擦力做负功，故两滑块组成系统的机械能不守恒，故A错误．重力对M做的功等于M重力势能的变化，合力对其做的功才等于M动能的增加，故B错误．m受到绳子的拉力向上运动，拉力做正功，故m 的机械能一定增加，而且轻绳对m做的功等于m机械能的增加，故C正确．根据功能原理得知：除重力、弹簧弹力以外的力做功，将导致机械能变化，摩擦力做负功，造成机械能损失．则两滑块组成系统的机械能损失等于M克服摩擦力做的功，故D正确．‎ ‎3．CD　小球运动过程中，只受重力，机械能守恒，若以桌面作为重力势能的参考平面，有E＝mv2，小球在最高点的动能为0，重力势能为mg(H－h)，所以机械能为mg(H－h)，故C、D正确．‎ ‎4．CD　半圆形槽光滑，两小球下滑过程中，均只有重力做功，机械能均守恒，即机械能均保持不变，故A错误；根据机械能守恒定律得mgr＝mv，即最低点的功能Ek1＝mgr，同理有Ek2＝mgR，由于R>r，则Ek1va>vb，选项C正确．‎ ‎6．C　小球运动到半圆弧最高点P时，重力恰好提供向心力，即mg＝m，所以vP＝，小球经过P后做平抛运动，下落时间t＝2 ，小球落地点离O点的水平距离为x＝vPt＝2R，所以选项C错误、A正确；小球从P点到落地的过程中，机械能守恒，所以落地时的动能mv2＝mv＋mg·2R＝，选项B正确；若将半圆弧轨道上部的1/4圆弧截去，其他条件不变，则小球离开轨道后做竖直上抛运动，设小球能达到的最大高度为h，则mgh＝，所以h＝，比P点高0.5R ‎，选项D正确．本题选不正确的，故选C.‎ ‎7．AD　由题意知，甲、乙两球组成的系统机械能守恒，故甲球减少的机械能总等于乙球增加的机械能，所以A正确；在甲下滑的过程中，甲、乙两球的动能在增加，故甲球减少的重力势能大于乙球增加的重力势能，所以B错误；由于甲的质量小于乙的质量，根据滑动过程机械能守恒知，甲不能下滑到最低点，所以C错误；根据滑动过程机械能守恒，杆从右向左滑回时，乙球一定能回到凹槽的最低点，故D正确．‎ ‎8．B　b摆动过程中满足机械能守恒，则有mbgL(1－cos60°)＝mbv2－0，在最低点有Tb－mbg＝mb，可得Tb＝2mbg.当a刚好对地面无压力时，有Ta＝mag，同一根绳Ta＝Tb，所以ma∶mb＝2∶1，故A、C、D错误、B正确．‎ ‎9．BD　m1由c点下滑到a点的过程中，沿绳子方向的速度是一样的，在m1滑下去一段距离后，绳子与圆的切线不重合，相当于圆的一根弦，所以此时两个小球的速度必然不相同，故A错误；重力的功率P＝mgv，这里的v是指m1的竖直分速度，一开始m1是由静止释放的，所以m1一开始的竖直速度为零，最后运动到a点的时候，由于此时的切线是水平的，所以此时的竖直速度也是零，但是m1由c到a的过程中是肯定有竖直速度的，所以相当于竖直速度是从无到有再到无的一个过程，也就是一个先变大后变小的过程，所以这个过程中重力的功率mgv先增大后减小，故B正确；若m1恰好能沿圆弧轨道下滑到a点，此时两小球速度均为零，根据动能定理得m1gR(1－cos60°)＝m2gR，解得m1＝2m2，故C错误、D正确．‎ ‎10．A　施加力F前，物块A、B整体静止，则2Mg＝kx，得x＝，施加力F的瞬间，对B，根据牛顿第二定律有kx－Mg－N＝Ma，得A、B间的弹力大小N＝M(g－a)，选项A正确；A、B在t1时刻分离，此时A、B具有共同的速度v与加速度a，且A、B间的弹力为零，对B有kx′－Mg＝Ma，得弹簧弹力kx′＝M(g＋a)≠0，选项B错误；A、B分离后，当弹簧弹力与重力平衡时B的速度最大，此时弹簧尚未恢复到原长，选项C错误；对B与弹簧组成的系统，A、B分离前A的压力对系统做负功，根据功能关系知系统机械能减少，选项D错误．‎ ‎11．解题思路：(1)小球从释放到O点过程中机械能守恒，则：mgR＝mv2‎ 解得：v＝＝5 m/s 小球在圆轨道最低点：FN－mg＝m 解得：FN＝mg＋m＝12 N 由牛顿第三定律，小球对轨道末端的压力FN′＝FN＝12 N ‎(2)小球从O点水平抛出后满足：‎ y＝gt2，x＝vt 又有y＝6－x2，联立解得：t＝ s.‎ 答案：(1)12 N　(2) s ‎12．解题思路：(1)小球运动到C处时，由牛顿第二定律得：F1－mg＝m 解得v1＝ 代入数据解得v1＝5 m/s 根据动能定理得：Ep－μmgx＝mv 代入解得Ep＝11.2 J ‎(2)小球从C到D过程，由机械能守恒 定律得：mv＝2mgR＋mv 代入数据解得v2＝3 m/s 由于v2>＝2 m/s，‎ 所以小球在D处对轨道外壁有压力，由 牛顿第二定律得：F2＋mg＝m 代入数据解得F2＝10 N 由牛顿第三定律得，小球对轨道的压力为10 N.‎ 答案：(1)11.2 J　(2)10 N 加餐练 ‎1．C　设小球的质量为m，绳长为L，根据动能定理得mgL＝mv2，解得v＝，LPmQ，LPmQ，所以P球所受绳的拉力大于Q球所受绳的拉力，故C项正确．向心加速度a＝＝2g，所以在轨迹的最低点，P、Q两球的向心加速度相同，故D项错误．‎ ‎2．AB　滑草车受力分析如图所示，在B点处有最大速度v，在上、下两段所受摩擦力大小分别为f1、f2‎ f1＝μmgcos45°‎ f2＝μmgcos37°‎ 整个过程由动能定理列方程：‎ mg·2h－f1·－f2·＝0①‎ 解得：μ＝，A项正确．‎ 滑草车在上段滑道运动过程由动能定理列方程：‎ mgh－f1·＝mv2②‎ 解得：v＝ ，B项正确．‎ 由①式知：Wf＝2mgh，C项错误．‎ 在下段滑道上，‎ mgsin37°－μmgcos37°＝ma2‎ 解得：a2＝－g，故D项错误．‎ ‎3．A　从绳恰好伸直到人第一次下降至最低点的过程中，人经历了先加速后减速的过程，当绳对人的拉力等于人的重力时速度最大，动能最大，之后绳的拉力大于人的重力，人向下减速到达最低点．绳对人的拉力始终向上，始终做负功．拉力的冲量向上，人的动量先增大后减小，综上所述，只有A选项正确．‎ ‎4．解题思路：(1)依题意，当弹簧竖直放置，长度被压缩至l时，质量为5m的物体的动能为零，其重力势能转化为弹簧的弹性势能．由机械能守恒定律，弹簧长度为l时的弹性势能为Ep＝5mgl①‎ 设P的质量为M，到达B点时的速度大小为vB，由能量守恒定律得 Ep＝Mv＋μMg·4l②‎ 联立①②式，取M＝m并代入题给数据得vB＝③‎ 若P能沿圆轨道运动到D点，其到达D点时的向心力不能小于重力，即P此时的速度大小v应满足－mg≥0④‎ 设P滑到D点时的速度为vD，由机械能守恒定律得 mv＝mv＋mg·2l⑤‎ 联立③⑤式得vD＝⑥‎ vD满足④式要求，故P能运动到D点，并从D点以速度vD水平射出．设P落回到轨道AB所需的时间为t，由运动学公式得2l＝gt2⑦‎ P落回到AB上的位置与B点之间的距离为s＝vDt⑧‎ 联立⑥⑦⑧式得s＝2l⑨‎ ‎(2)为使P能滑上圆轨道，它到达B点时的速度应大于零．‎ 由①②式可知5mgl>μMg·4l 要使P仍能沿圆轨道滑回，P在圆轨道上的上升高度不能超过半圆轨道的中点C.由机械能守恒定律有Mv≤Mgl⑪‎ 联立①②⑩⑪式得m≤M