【物理】2019届二轮复习第54讲光的折射全反射光导纤维教案（全国通用） 4页

第54讲 光的折射 全反射 光导纤维 ‎【教学目标】‎ ‎1.理解折射率的概念，掌握光的折射定律.‎ ‎2.掌握全反射的条件，会进行有关简单的计算． ‎ ‎【教学过程】‎ ‎ ‎ ‎★重难点一、折射定律及折射率的理解★‎ ‎1．对折射率的理解 ‎(1)公式n＝中，不论是光从真空射入介质，还是从介质射入真空，i总是真空中的光线与法线间的夹角，r总是介质中的光线与法线间的夹角。‎ ‎(2)折射率由介质本身性质决定，与入射角的大小无关。‎ ‎(3)折射率与介质的密度没有关系，光密介质不是指密度大的介质。‎ ‎(4)折射率的大小不仅与介质本身有关，还与光的频率有关。同一种介质中，频率越大的色光折射率越大，传播速度越小。‎ ‎(5)同一种色光，在不同介质中虽然波速、波长不同，但频率相同。‎ ‎2．平行玻璃砖、三棱镜和圆柱体(球)对光路的控制 平行玻璃砖 三棱镜 圆柱体(球)‎ 结构 玻璃砖上下表面是平行的 横截面为三角形的三棱镜 横截面是圆 对光线的作用 通过平行玻璃砖的光线不改变传播方向，但要发生侧移 通过三棱镜的光线经两次折射后，出射光线向棱镜底面偏折 圆界面的法线是过圆心的直线，经过两次折射后向圆心偏折 应用 测定玻璃的折射率 全反射棱镜，改变光的传播方向 改变光的传播方向 ‎3.解决光的折射问题的思路 ‎(1)根据题意画出正确的光路图。‎ ‎(2)利用几何关系确定光路中的边、角关系，要注意入射角、折射角均以法线为标准。‎ ‎(3)利用折射定律、折射率公式求解。‎ ‎(4)注意：在折射现象中光路是可逆的。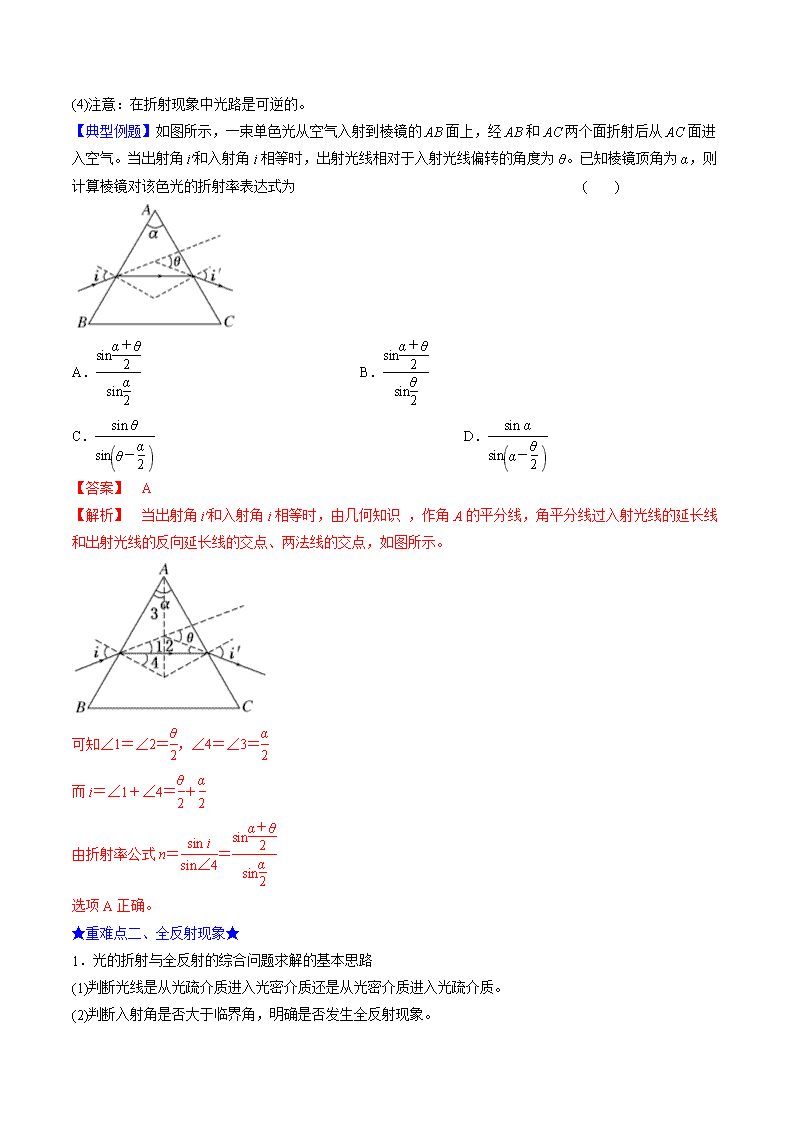‎ ‎【典型例题】如图所示，一束单色光从空气入射到棱镜的AB面上，经AB和AC两个面折射后从AC面进入空气。当出射角i′和入射角i相等时，出射光线相对于入射光线偏转的角度为θ。已知棱镜顶角为α，则计算棱镜对该色光的折射率表达式为 (　　)‎ A．　　　　　 B． C． D． ‎【答案】　A ‎【解析】　当出射角i′和入射角i相等时，由几何知识 ，作角A的平分线，角平分线过入射光线的延长线和出射光线的反向延长线的交点、两法线的交点，如图所示。‎ 可知∠1＝∠2＝，∠4＝∠3＝ 而i＝∠1＋∠4＝＋ 由折射率公式n＝＝ 选项A正确。‎ ‎★重难点二、全反射现象★‎ ‎1．光的折射与全反射的综合问题求解的基本思路 ‎(1)判断光线是从光疏介质进入光密介质还是从光密介质进入光疏介质。‎ ‎(2)判断入射角是否大于临界角，明确是否发生全反射现象。‎ ‎(3)画出反射、折射或全反射的光路图，必要时还可应用光路的可逆原理画出光路图，然后结合几何知识进行推断和求解相关问题。‎ ‎(4)折射率n是讨论折射和全反射问题的重要物理量，是联系各物理量的桥梁，对跟折射率有关的所有关系式应熟练掌握。‎ ‎2．求解光的折射、全反射问题的四点提醒 ‎(1)光密介质和光疏介质是相对而言的。同一种介质，相对于其他不同的介质，可能是光密介质，也可能是光疏介质。‎ ‎(2)如果光线从光疏介质进入光密介质，则无论入射角多大，都不会发生全反射现象。‎ ‎(3)在光的反射和全反射现象中，均遵循光的反射定律，光路均是可逆的。‎ ‎(4)当光射到两种介质的界面上时，往往同时发生光的折射和反射现象，但在全反射现象中，只发生反射，不发生折射。‎ ‎3．求解全反射现象中光的传播时间的一般思路 ‎(1)全反射现象中，光在同种均匀介质中的传播速度不发生变化，即v＝。‎ ‎(2)全反射现象中，光的传播路程应结合光路图与几何关系进行确定。‎ ‎(3)利用t＝求解光的传播时间。‎ ‎4．解决全反射问题的一般方法 ‎(1)确定光是从光密介质进入光疏介质。‎ ‎(2)应用sin C＝确定临界角。‎ ‎(3)根据题设条件，判定光在传播时是否发生全反射。‎ ‎(4)如发生全反射，画出入射角等于临界角时的临界光路图。‎ ‎(5)运用几何关系或三角函数关系以及反射定律等进行分析、判断、运算，解决问题。‎ ‎5.解答全反射类问题的技巧 ‎(1)解答全反射类问题时，要抓住发生全反射的两个条件。‎ ‎①光必须从光密介质射入光疏介质；‎ ‎②入射角大于或等于临界角。‎ ‎(2)利用好光路图中的临界光线，准确地判断出恰好发生全反射的光路图是解题的关键，且在作光路图时尽量与实际相符。‎ ‎【典型例题】一厚度为h的大平板玻璃水平放置，其下表面贴有一半径为r的圆形发光面。在玻璃板上表面放置一半径为R的圆纸片，圆纸片与圆形发光面的中心在同一竖直线上。已知圆纸片恰好能完全遮挡住从圆形发光面发出的光线(不考虑反射)，求平板玻璃的折射率。‎ ‎【答案】 ‎【解析】如图所示，考虑从圆形发光面边缘的A点发出的一条光线，假设它斜射到玻璃上表面的A′点发生折射，‎ 根据折射定律有nsin θ＝sin α①‎ 式中，n是玻璃的折射率，θ是入射角，α是折射角。现假设A′恰好在纸片边缘。由题意，在A′点刚好发生全反射，故α＝②‎ 设AA′线段在玻璃上表面的投影长为L，由几何关系有 sin θ＝③‎ 由题意，纸片的半径应为R＝L＋r④‎ 联立以上各式得n＝ ⑤‎