热点05+平抛运动和运动合成-40热点2019年高考名校物理模拟试题分项解析 7页

一．选择题 ‎1. （2019武汉调研）在光滑的水平面上，质量 m=1kg的物块在 F =2N 的水平恒力作用下运动，如图所示为物块的一段轨迹。已知物块经过 P、Q两点时的速率均为v＝4m/s ，且物块在 P 点的速度方向与PQ连线的夹角a = 30°。关于物块的运动，下列说法正确的是 A.水平恒力F的方向与PQ连线成60°夹角 ‎ B.物块从P点运动到Q点的时间为2s C.物块从P点运动到Q 点的过程中最小速率为 2 m/s D .P、Q两点的距离为8 m ‎ ‎【参考答案】B ‎【命题意图】本题考查运动的分解及其相关知识点。‎ ‎【解题策略】把此题的情景类比于斜上抛运动，PQ连线即为平行于水平面的直线，可降低解题思维难度。‎ ‎2．（2018高考全国理综III）在一斜面顶端，将甲乙两个小球分别以v和的速度沿同一方向水平抛出，两球都落在该斜面上。甲球落至斜面时的速率是乙球落至斜面时速率的 A．2倍 B．4倍 ‎ C．6倍 D．8倍 ‎【参考答案】B ‎【命题意图】本题考查平抛运动规律、机械能守恒定律及其相关的知识点。‎ ‎【解题思路】设甲球落至斜面时的速率为v1，乙落至斜面时的速率为v2，由平抛运动规律，x=vt，y=gt2，设斜面倾角为θ，由几何关系，tanθ=y/x，小球由抛出到落至斜面，由机械能守恒定律，mv2+mgy=mv12，联立解得：v1=·v，即落至斜面时的速率与抛出时的速率成正比。同理可得，v2=·v/2，所以甲球落至斜面时的速率是乙球落至斜面时的速率的2倍，选项A正确。 ‎ ‎2．现有一根不可伸长的轻质细绳，绳长L=‎1m。绳的一端固定于O点，另一端系着质量m=‎ ‎1kg的可看着质点的小球，将小球拉到O点正上方的A点处静止，此时绳子刚好伸直且无张力，若小球从A点以v1=‎1m/s的水平速度抛出。不计小球在运动中所受的阻力，重力加速度g=‎10m/s2。则小球运动到最低点时绳对它的拉力大小是：‎ A.10N B.21.64N C. 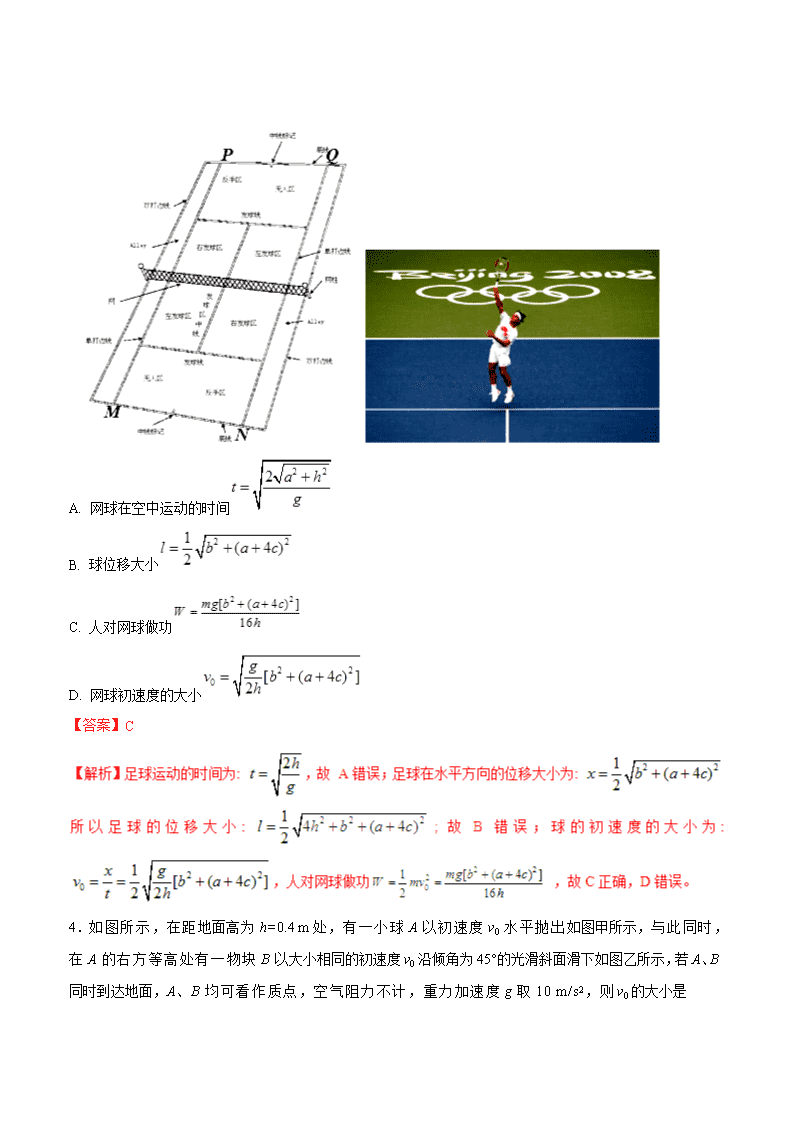31.64N D.51N ‎【答案】C ‎3.如图所示，是网球比赛场地图，单打区域长MP为a，宽MN 为b，发球线到网的距离为c，一个球员站在发球线的中点发球，将球打到对方左下方死角（单打边线与底线的交点），若球击球点的高度为h．网球被顶出后做平抛运动（球可看做质点，不计空气的阻力），重力加速度为g。则下列说法正确的是 A. 网球在空中运动的时间 B. 球位移大小 C. 人对网球做功 D. 网球初速度的大小 ‎【答案】C ‎4．如图所示，在距地面高为h=0.4 m处，有一小球A以初速度v0水平抛出如图甲所示，与此同时，在A的右方等高处有一物块B以大小相同的初速度v0沿倾角为45°的光滑斜面滑下如图乙所示，若A、B同时到达地面，A、B均可看作质点，空气阻力不计，重力加速度g取10 m/s2，则v0的大小是 A．1 m/s B． m/s C．2 m/s D．2 m/s ‎【答案】A ‎ ‎5．如图所示，在高尔夫球场上，某人从高出水平地面h的坡顶以速度v0水平击出一球，球落在水平地面上的C点。已知斜坡AB与水平面的夹角为θ，不计空气阻力。则下列说法正确的是 ‎ A．若球落到斜坡上，其速度方向与水平方向的夹角为定值 B．若球落到斜坡上，其速度方向与水平方向的夹角不确定 C．AC的水平距离为 D．小球落在C点时的速度大小为 ‎【答案】A ‎ ‎【解析】若球落到斜面上，由平抛运动规律有，设速度与水平方向的夹角为，由平抛运动规律有，比较得=定值，选项A正确，选项B错误；球从A运动到C做平抛运动，竖直方向有，水平方向有，选项C错误；根据动能定理有 ‎，解得，故选项D错误。 ‎ 根据牛顿第二定律， ，得 （1分）‎ 根据匀变速运动的规律，，得v = 3.0 m/s （2分）‎ ‎（2）根据匀变速直线运动的规律， ，得l = 1.4 m （2分）‎ ‎2．（2019四川资阳一诊）（12分）‎ 如图所示，在E＝103V/m的竖直匀强电场中，有一光滑半圆形绝缘轨道QPN与一水平绝缘轨道MN在N点平滑相接，半圆形轨道平面与电场线平行，其半径R＝‎0.4 ‎m，N为半圆形轨道最低点，一带负电且电荷量q＝10－‎4 C的小滑块，质量m＝‎0.01 kg，与水平轨道间的动摩擦因数μ＝0.15，位于N点右侧d＝‎1.5 m的M处，若给小滑块一个初速度v0向左运动，小滑块恰能通过半圆形轨道的最高点Q。取g=‎10 m/s2，求：‎ ‎（1）小滑块的初速度v0；‎ ‎（2）小滑块通过Q点后落回水平轨道时落点S距N的水平距离x。‎ ‎【名师解析】（12分）解：‎ ‎（1）设小滑块恰能到达Q点时速度为v，由牛顿第二定律得：‎ ‎ ……………………①‎ 小滑块从开始运动至到达Q点过程中，由动能定理得：‎ ‎ ……………………②‎ 联解①②得：‎ ‎ ……………………③‎ ‎3.（2018浙江温州期末）如图所示，倾角为37°的粗糙斜面AB底端与半径R=‎0.4m的光滑半圆轨道BC平滑相连，O点为轨道圆心，BC为圆轨道直径且处于竖直方向，A、C两点等高。质量m=‎0.4kg的滑块从A点由静止开始下滑，恰能滑到与O点等高的D点，g取‎10m/s2，sin37°=0.6，cos37°=0.8．求：‎ ‎（1）求滑块与斜面间的动摩擦因数μ；‎ ‎（2）如果滑块到达C点时对轨道压力为3N，求滑块从A点沿斜面滑下时初速度v0大小；‎ ‎（3）如果在A点给滑块沿斜面向下的初速度，使滑块能沿着圆轨道从C点离开轨道，落到AB斜面上，求滑块从C点飞出至落到斜面上所经历的最长时间。‎ ‎【名师解析】（1）滑块由A到D过程，根据动能定理，有：‎ mgR﹣μmgcos37°•=0‎ 代入数据解得：μ=tan37°=0.375‎ ‎（2）滑块到达C点时，根据牛顿第二定律有：‎ FN+mg=m 据题可得 FN=3N 从A到C的过程，由动能定理有：‎ ‎﹣μmgcos37°•=﹣‎ 联立可得 v0=3m/s ‎