【物理】2018届二轮复习纵谈单摆的衍变学案（全国通用） 3页

第 4 点　纵谈单摆的衍变 单摆的周期公式 T＝2π l g，在一些情况中会有一些变化，l 为悬点到质心的距离，g 有时不 是重力加速度，而是在某些情景中的等效重力加速度 g′. 1．等效加速度 g′的变化引起单摆衍变 等效加速度通常有以下两种情况： (1)在其他星球表面 g′＝GM r2 ，M、r 分别为该星球的质量和半径． (2)单摆处于超重或失重状态下的等效重力加速度分别为 g′＝g＋a，g′＝g－a. 在其他复杂物理环境中也可以这样计算：g′等于单摆静止时摆线的张力除以摆球的质量． 2．摆长 l 的变化引起单摆的衍变 l 为等效摆长：摆动圆弧的圆心到摆球重心的距离． (1)球的半径为 r，双线摆的摆长 l＝r＋Lcos α，如图 1 所示． 图 1 (2)如图 2 所示，球在半径为 R 的光滑圆弧槽靠近最低点 A 振动(球的半径 r≪R)：l＝R. 图 2 3．摆动过程的不对称引起单摆的衍变 如图 3 所示，有一单摆绳长为 L，在悬点正下方L 2处有一个能挡住摆线的钉子，则此单摆摆动 的周期为： T＝1 2(2π L g＋2π L 2 g )＝( 2＋1)π L 2g. 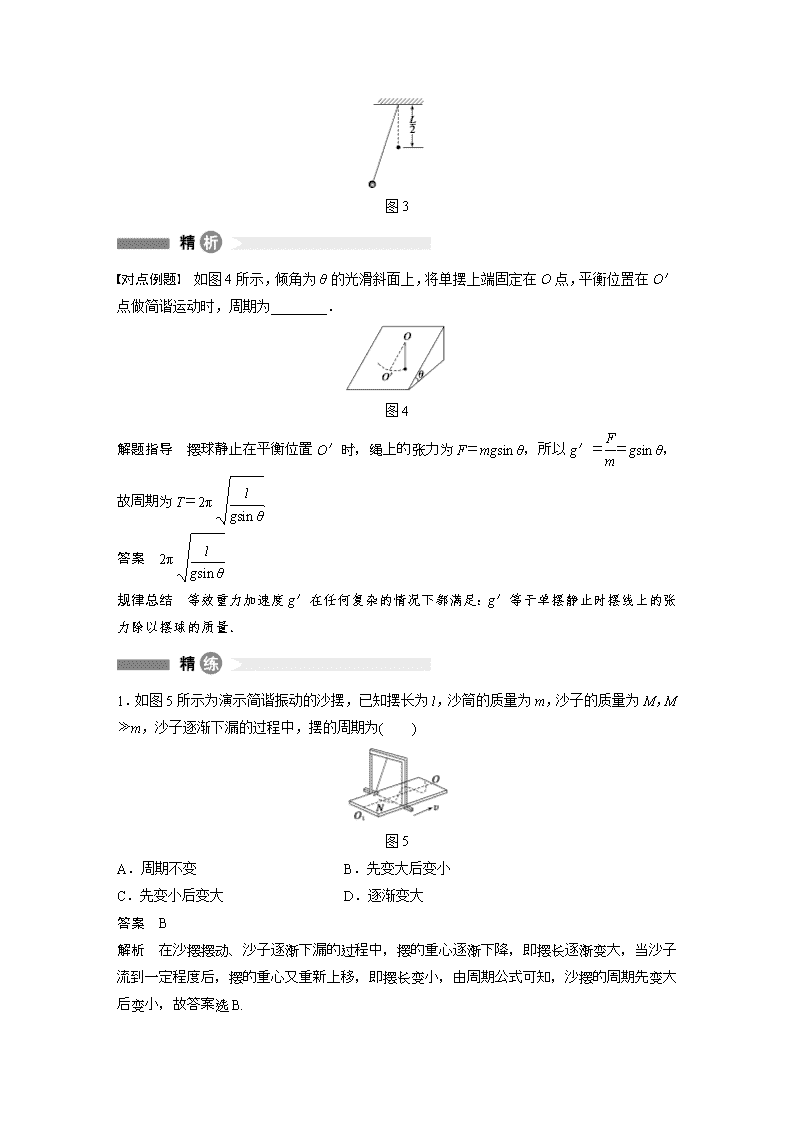图 3 对点例题 　如图 4 所示，倾角为 θ 的光滑斜面上，将单摆上端固定在 O 点，平衡位置在 O′ 点做简谐运动时，周期为________． 图 4 解题指导　摆球静止在平衡位置 O′时，绳上的张力为 F＝mgsin θ，所以 g′＝F m＝gsin θ， 故周期为 T＝2π l gsin θ. 答案　2π l gsin θ 规律总结　等效重力加速度 g′在任何复杂的情况下都满足：g′等于单摆静止时摆线上的张 力除以摆球的质量． 1．如图 5 所示为演示简谐振动的沙摆，已知摆长为 l，沙筒的质量为 m，沙子的质量为 M， M≫m，沙子逐渐下漏的过程中，摆的周期为(　　) 图 5 A．周期不变 B．先变大后变小 C．先变小后变大 D．逐渐变大 答案　B 解析　在沙摆摆动、沙子逐渐下漏的过程中，摆的重心逐渐下降，即摆长逐渐变大，当沙子 流到一定程度后，摆的重心又重新上移，即摆长变小，由周期公式可知，沙摆的周期先变大 后变小，故答案选 B. 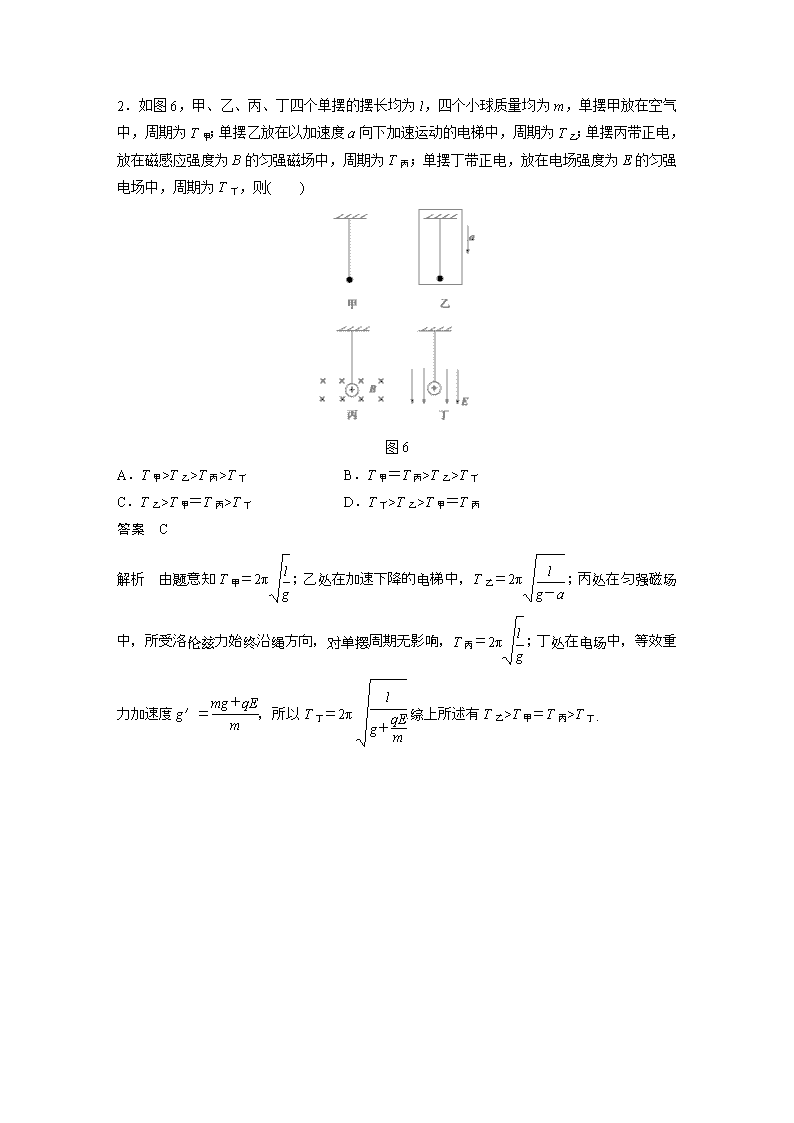2．如图 6，甲、乙、丙、丁四个单摆的摆长均为 l，四个小球质量均为 m，单摆甲放在空气 中，周期为 T 甲；单摆乙放在以加速度 a 向下加速运动的电梯中，周期为 T 乙；单摆丙带正电， 放在磁感应强度为 B 的匀强磁场中，周期为 T 丙；单摆丁带正电，放在电场强度为 E 的匀强 电场中，周期为 T 丁，则(　　) 图 6 A．T 甲>T 乙>T 丙>T 丁 B．T 甲＝T 丙>T 乙>T 丁 C．T 乙>T 甲＝T 丙>T 丁 D．T 丁>T 乙>T 甲＝T 丙 答案　C 解析　由题意知 T 甲＝2π l g；乙处在加速下降的电梯中，T 乙＝2π l g－a；丙处在匀强磁场中， 所受洛伦兹力始终沿绳方向，对单摆周期无影响，T 丙＝2π l g；丁处在电场中，等效重力加 速度 g′＝mg＋qE m ，所以 T 丁＝2π l g＋qE m .综上所述有 T 乙>T 甲＝T 丙>T 丁．