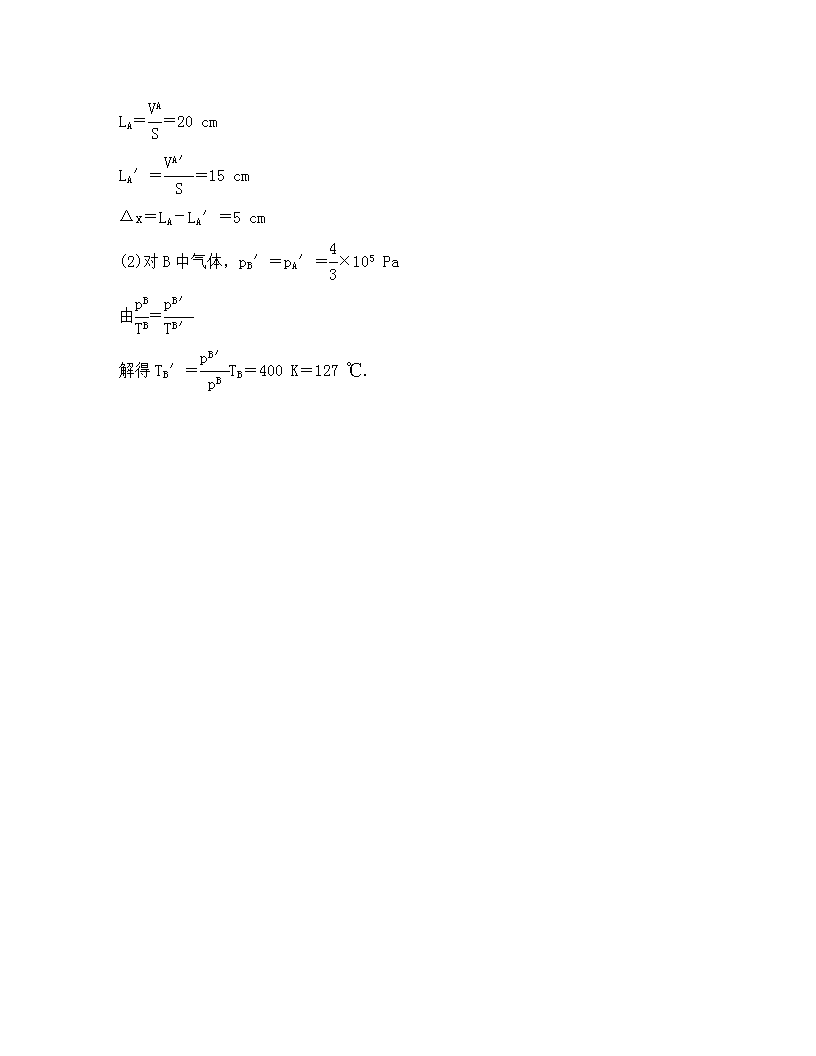高中物理 模块要点回眸 第15点 液柱移动方向的判断方法素材 粤教版选修3-3（通用） 3页

第15点　液柱移动方向的判断方法 ‎ 用液柱或活塞隔开的两部分气体，当气体温度变化时，往往气体的状态参量p、V、T都要发生变化，直接判断液柱或活塞的移动方向比较困难，通常先进行气体状态的假设，然后应用查理定律求解．其一般思路为：‎ ‎1．先假设液柱或活塞不发生移动，两部分气体均做等容变化．‎ ‎2．对两部分气体分别应用查理定律的分比式Δp＝p，求出每部分气体压强的变化量Δp，并加以比较．‎ 对点例题　粗细均匀，两端封闭的细长玻璃管中，有一段水银柱将管中气体分为A和B两部分，如图1所示，已知两部分气体A和B的体积关系是VB＝3VA，且开始时温度相同，将玻璃管两端的气体温度均升高相同温度的过程中，水银将(　　) 图1‎ A．向A端移动 B．向B端移动 C．始终不动 D．以上三种情况都有可能 解题指导　假设水银柱不发生移动，则两部分均做等容变化，由查理定律的分比式Δp＝p判断．由于pA＝pB，ΔTA＝ΔTB，TA＝TB，所以ΔpA＝ΔpB所以水银柱始终不动，故假设正确．‎ 答案　C 特别提醒　此例题中是两边升温且液柱两边横截面积相等．所以只需比较压强的变化量．若是降温或液柱两边横截面积不相等，则应注意比较变化后液柱两边受力的大小，具体分析如下：‎ ‎(1)如果液柱两端的横截面积相等，且Δp均大于零，意味着两部分气体的压强均增大，则液柱向Δp值较小的一方移动；若Δp均小于零，意味着两部分气体的压强均减小，则液柱向压强减小量较大的一方(即|Δp|较大的一方)移动；若Δp相等，则液柱不移动．‎ ‎(2)如果液柱两端的横截面积不相等，则应考虑液柱两端的受力变化(ΔpS)．若Δp均大于零，则液柱向ΔpS较小的一方移动；若Δp均小于零，则液柱向|ΔpS|值较大的一方移动；若ΔpS相等，则液柱不移动．‎ 如图2所示，A气缸横截面积为‎500 cm2，A、B两个气缸中装有体积均为‎10 L、压强均为1 atm、温度均为‎27 ℃‎的理想气体，中间用细管连接．细管中有一绝热活塞M，细管容积不计．现给左边的活塞N施加一个推力，使其缓慢向右移动，同时给B中气体加热，使此过程中A汽缸中的气体温度保持不变，活塞M保持在原位置不动．不计活塞与器壁、细管间的摩擦，周围大气压强为1 atm＝105 Pa，当推力F＝×103 N时，求： 图2‎ ‎(1)活塞N向右移动的距离是多少厘米？‎ ‎(2)B气缸中的气体升温到多少摄氏度？‎ 答案　(1)‎5 cm　(2)‎‎127 ℃‎ 解析　(1)pA′＝pA＋＝×105 Pa 对A中气体，由pAVA＝pA′VA′‎ 得VA′＝，解得VA′＝VA LA＝＝‎‎20 cm LA′＝＝‎‎15 cm Δx＝LA－LA′＝‎‎5 cm ‎(2)对B中气体，pB′＝pA′＝×105 Pa 由＝ 解得TB′＝TB＝400 K＝127 ℃.‎