专题16-16 原子和原子核中的非选择题-2019年高考物理100考点最新模拟题千题精练 9页

‎100考点最新模拟题千题精练16-16‎ 第十六部分 选修3-5‎ 十六、原子和原子核中的非选择题 ‎1． (8分)(2013·山东理综)恒星向外辐射的能量来自于其内部发生的各种热核反应，当温度达到108 K时，可以发生“氦燃烧”。‎ ‎(1)完成“氦燃烧”的核反应方程：He＋________―→Be＋γ；‎ ‎(2)Be是一种不稳定的粒子，其半衰期为2.6×10－16 s。一定质量的Be，经7.8×10－16 s后所剩Be占开始时的________。‎ 答案　(1)He　(2) ‎2． (9分)(2016·泰安质检)氘核H和氚核H结合成氦核He的核反应方程如下：‎ H＋H―→He＋n＋17.6 MeV ‎(1)这个核反应称为________。‎ ‎(2)要发生这样的核反应，需要将反应物质的温度加热到几百万开尔文。式中17.6 MeV是核反应中________(选填“放出”或“吸收”)的能量，核反应后生成物的总质量比核反应前物质的总质量________(选填“增加”或“减少”)了________kg。‎ ‎【名师解析】H＋H―→He＋n＋17.6 MeV为轻核聚变反应，17.6 MeV是反应中放出的能量，再由ΔE＝Δmc2可知，质量减少Δm＝＝3.1×10－‎29 kg。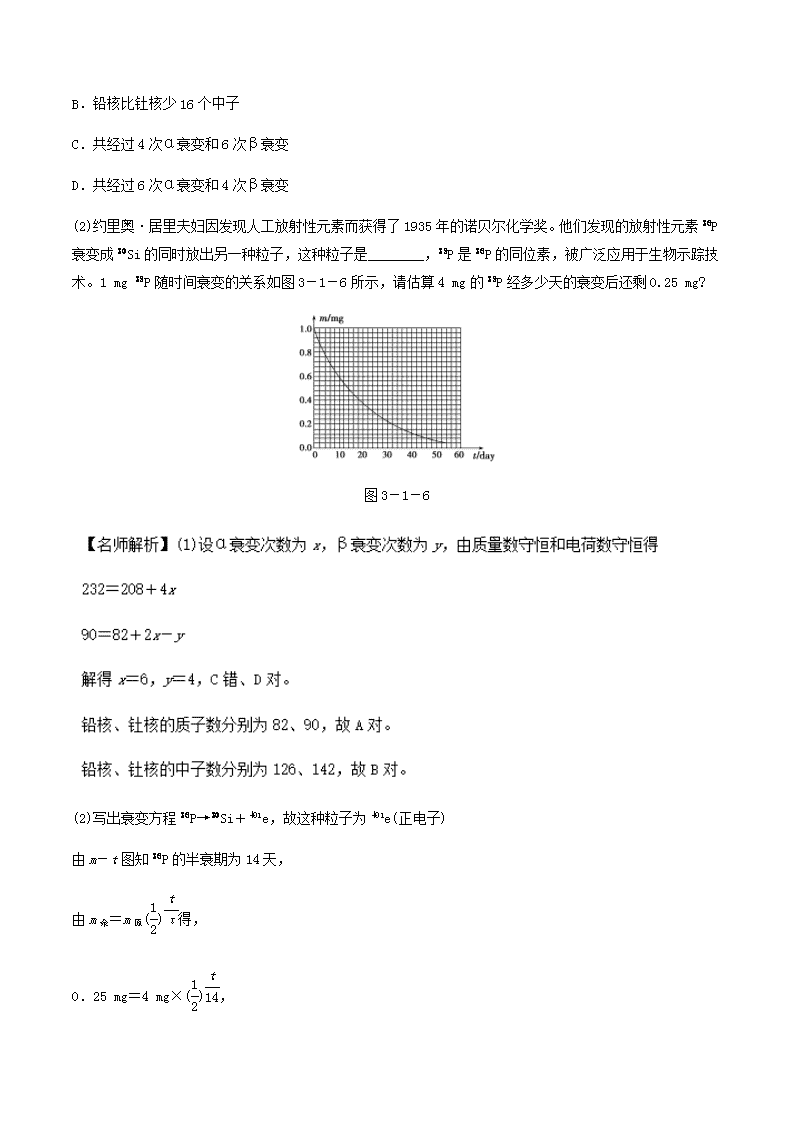‎ 答案　(1)聚变　(2)放出　减少　3.1×10－29‎ ‎3.(1)Th(钍)经过一系列α衰变和β衰变，变成Pb(铅)，下列说法正确的是 A．铅核比钍核少8个质子 B．铅核比钍核少16个中子 C．共经过4次α衰变和6次β衰变 D．共经过6次α衰变和4次β衰变 ‎(2)约里奥·居里夫妇因发现人工放射性元素而获得了1935年的诺贝尔化学奖。他们发现的放射性元素P衰变成Si的同时放出另一种粒子，这种粒子是________，P是P的同位素，被广泛应用于生物示踪技术。1 mg P随时间衰变的关系如图3－1－6所示，请估算4 mg的P经多少天的衰变后还剩0.25 mg?‎ 图3－1－6‎ ‎ ‎ ‎(2)写出衰变方程P→Si＋e，故这种粒子为e(正电子)‎ 由m－t图知P的半衰期为14天，‎ 由m余＝m原()得，‎ ‎0．25 mg＝4 mg×()，‎ 故t＝56天。‎ ‎【答案】(1)ABD　(2)正电子　(e)　56天 ‎4.现有以下五个核反应：‎ A.H＋H―→He＋n B.92U＋n―→X＋Kr＋3n C.Na―→Mg＋　0－1e D.88Ra―→86Rn＋He E.He＋Be―→‎6C＋n ‎(1)________是发现中子的核反应方程，________是研究原子弹的基本核反应方程，________是研究氢弹的基本核反应方程；‎ ‎(2)求B项中X的质量数和中子数；‎ ‎(3)判断以上五个核反应的反应类型。‎ ‎【答案】(1)E　B　A　(2)144　88‎ ‎(3)A.聚变　B．裂变　C．β衰变　D．α衰变　E．人工转变 ‎5．（2018山西吕梁市孝义市一模）如图所示，在虚线HF上方存在着垂直于纸面向里的匀强磁场B1，在x轴上方存在沿x轴正方向的匀强电场，在x轴下方的矩形区域ABCD内还存在垂直于纸面向外的匀强磁场，矩形区域的AB边与x轴重合。M点是HF和y轴的交点，在M点有一静止镭核（Ra），某时刻发生放射性衰变，放出某种质量为m、电荷量为q的粒子后变为一氡核（Rn），氡核恰好沿y轴正向做匀速直线运动，粒子则以初速度v0‎ 沿y轴负方向运动，恰好从N点进入磁场，当粒子第二次经过x轴时电场反向，粒子恰好回到M点，若|OM|=2|ON|，核子的质量数与质量成正比，不计氡核和粒子的重力。‎ ‎（1）写出上述过程中镭核的衰变方程。‎ ‎（2）求电场强度的大小E。‎ ‎（3）求N点的横坐标x。‎ ‎（4）求矩形区域ABCD内匀强磁场的磁感应强度的大小B2及矩形区域的最小面积S。‎ ‎（3）粒子从M点到N点做类平抛运动，设运动时间为t，O点到N点的距离为x，则 沿y轴负方向有：2x=v0t1‎ 沿x轴正方向有：x=at1‎ 又有：a=‎ 解得：x=‎ 由几何关系得粒子在磁场中做周运动的半径R=‎ 由牛顿第二定律得：qvB2=m 解得：B2=‎ 矩形区域的最小面积为S=2R（R+x） ‎ 解得：S=‎ 答：（1）上述过程中镭核的衰变方程是：→+。‎ ‎（2）电场强度的大小E是。‎ ‎（3）N点的横坐标x为。‎ ‎（4）矩形区域ABCD内匀强磁场的磁感应强度的大小B2及矩形区域的最小面积S为。‎ ‎6．(14分)在磁感应强度为B的匀强磁场中，一个静止的放射性原子核发生了一次α衰变。放射出的α粒子(He)在与磁场垂直的平面内做圆周运动，其轨道半径为R。以m、q分别表示α粒子的质量和电荷量。‎ ‎(1)放射性原子核用X表示，新核的元素符号用Y表示，写出该α衰变的核反应方程。‎ ‎(2)α粒子的圆周运动可以等效成一个环形电流，求圆周运动的周期和环形电流大小。‎ ‎(3)设该衰变过程释放的核能都转化为α粒子和新核的动能，新核的质量为M，求衰变过程的质量亏损Δm。‎ ‎【名师解析】(1)X―→Y＋He。‎ 设衰变后新核Y的速度大小为v′，系统动量守恒 Mv′－mv＝0‎ v′＝＝ 由Δmc2＝Mv′2＋mv2‎ 得Δm＝。‎ ‎7.(2016·深圳模拟)某些建筑材料可产生放射性气体——氡，氡可以发生α或β衰变，如果人长期生活在氡浓度过高的环境中，那么，氡经过人的呼吸道沉积在肺部，并放出大量的射线，从而危害人体健康。原来静止的氡核(Rn)发生一次α衰变生成新核钋(P0)，并放出一个能量为E0＝0.09 MeV的光子。已知放出的α粒子动能为Eα＝5.55 MeV；忽略放出光子的动能，但考虑其能量；1 u＝931.5 MeV/c2。‎ ‎(1)写出衰变的核反应方程；‎ ‎(2)衰变过程中总的质量亏损为多少？(保留三位有效数字)。‎ ‎【名师解析】(1)衰变方程为：Rn→Po＋He；‎ ‎(2)忽略放出光子的动量，根据动量守恒定律，0＝pα＋pP0，‎ 即新核钋(P0)的动量与α粒子的动量大小相等，又Ek＝，‎ 可求出新核钋(P0)的动能为EP0＝Eα 由题意，质量亏损对应的能量以光子的能量和新核、α粒子动能形式出现衰变时释放出的总能量为ΔE＝Eα＋EP0＋E0＝Δmc2‎ 故衰变过程中总的质量亏损是Δm＝＝0.006 16 u。‎ ‎【答案】(1)Rn→Po＋He　(2)0.006 16 u ‎8．为确定爱因斯坦的质能方程ΔE＝Δmc2的正确性，设计了如下实验：用动能为E1＝0.60 MeV的质子轰击静止的锂核Li，生成两个α粒子，测得两个α粒子的动能之和为E2＝19.9 MeV，已知质子、α粒子、锂粒子的质量分别取mp＝1.007 3 u、mα＝4.001 5 u、mLi＝7.016 0 u，求：‎ ‎(1)写出核反应方程．‎ ‎(2)通过计算说明ΔE＝Δmc2正确．(1 u相当于931.5 MeV)‎ ‎【参考答案】(1)Li＋H→2He　(2)见解析 ‎9.一个静止的氡核Rn放出一个α粒子后衰变为钋核Po，同时放出能量为E＝0.09 MeV的光子．假设放出的核能完全转变为钋核与α粒子的动能，不计光子的动量．已知M氡＝222.086 63 u、mα＝4.002 6 u、M钋＝218.076 6 u，1 u相当于931.5 MeV的能量．‎ ‎(1)写出上述核反应方程；‎ ‎(2)求出发生上述核反应放出的能量；‎ ‎(3)确定钋核与α粒子的动能．‎ ‎【参考答案】(1)Rn→Po＋He＋γ　(2)6.92 MeV ‎(3)0.12 MeV　6.71 MeV ‎【名师解析】(1)Rn→Po＋He＋γ.‎ ‎(2)质量亏损Δm＝222.086 63 u－4.002 6 u－218.076 6 u＝0.007 43 u ΔE＝Δmc2＝0.007 43×931.5 MeV＝6.92 MeV.‎ ‎(3)设α粒子、钋核的动能分别为Ekα、Ek钋，动量分别为pα、p钋，由能量守恒定律得：ΔE＝Ekα＋Ek钋＋E 不计光子的动量，由动量守恒定律得：‎ ‎0＝pα＋p钋 又Ek＝，故Ekα∶Ek钋＝218∶4‎ 联立解得Ek钋＝0.12 MeV，Ekα＝6.71 MeV.‎ ‎10．钚的放射性同位素Pu静止时衰变为铀核激发态U*和α粒子，而铀核激发态U*立即衰变为铀核U，并放出能量为0.097 MeV的γ光子。已知：Pu、U和α粒子的质量分别为mPu＝239.052 1 u、mU＝235.043 9 u和mα＝4.002 6 u，1 u的质量相当于931.5 MeV的能量。‎ ‎(1)写出衰变方程；‎ ‎(2)已知衰变放出的光子的动量可忽略，求α粒子的动能。‎ ‎【名师解析】(1)衰变方程为 Pu→U*＋He U*→U＋γ 或合起来有Pu→U＋He＋γ 答案　(1)见解析　(2)5.034 MeV ‎10．三个α粒子结合成一个碳C，已知碳原子的质量为12.000 0 u，氦原子质量为4.002 6 u。‎ ‎(1)写出核反应方程；‎ ‎(2)这个核反应放出的能量是多少焦？‎ ‎(3)这个能量合多少MeV?‎ 答案　(1)3He→C＋ΔE ‎(2)1.165×10－12 J ‎(3)7.28 MeV