- 654.00 KB
- 2021-05-27 发布
- 1、本文档由用户上传,淘文库整理发布,可阅读全部内容。
- 2、本文档内容版权归属内容提供方,所产生的收益全部归内容提供方所有。如果您对本文有版权争议,请立即联系网站客服。
- 3、本文档由用户上传,本站不保证质量和数量令人满意,可能有诸多瑕疵,付费之前,请仔细阅读内容确认后进行付费下载。
- 网站客服QQ:403074932
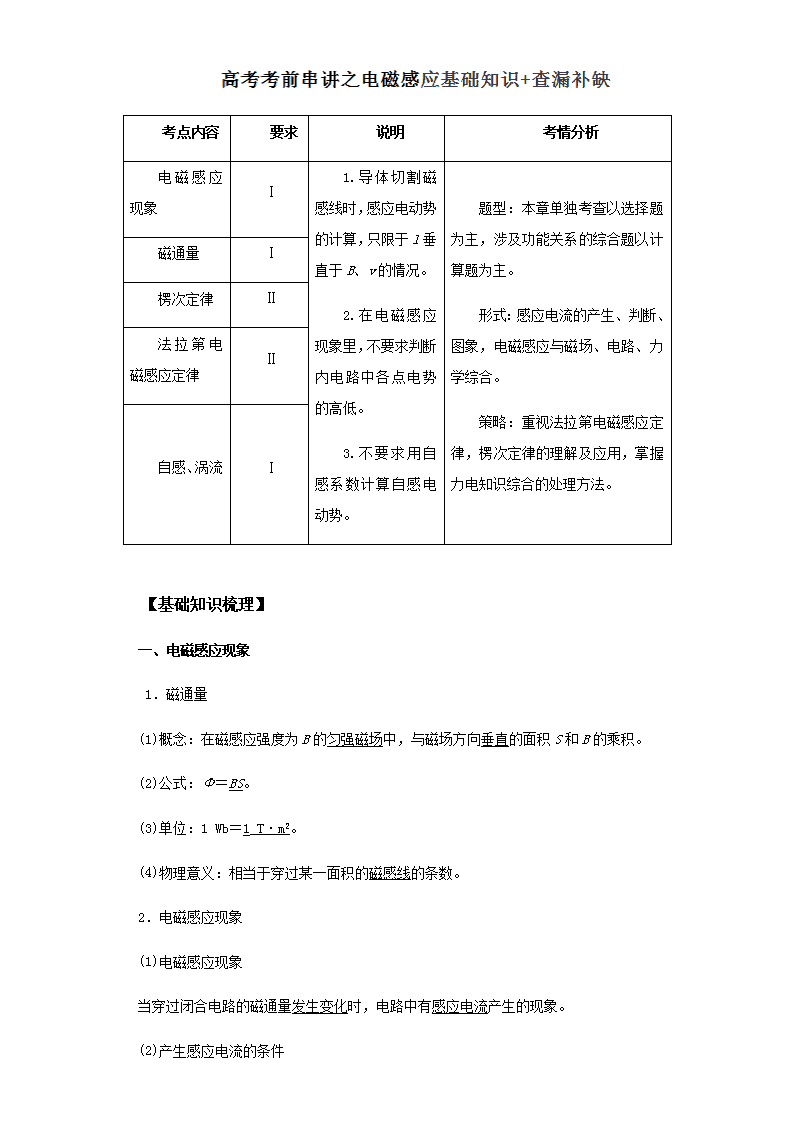
考点内容
要求
说明
考情分析
电磁感应现象
Ⅰ
1.导体切割磁感线时,感应电动势的计算,只限于l垂直于B、v的情况。
2.在电磁感应现象里,不要求判断内电路中各点电势的高低。
3.不要求用自感系数计算自感电动势。
题型:本章单独考查以选择题为主,涉及功能关系的综合题以计算题为主。
形式:感应电流的产生、判断、图象,电磁感应与磁场、电路、力学综合。
策略:重视法拉第电磁感应定律,楞次定律的理解及应用,掌握力电知识综合的处理方法。
磁通量
Ⅰ
楞次定律
Ⅱ
法拉第电磁感应定律
Ⅱ
自感、涡流
Ⅰ
【基础知识梳理】
一、电磁感应现象
1.磁通量
(1)概念:在磁感应强度为B的匀强磁场中,与磁场方向垂直的面积S和B的乘积。
(2)公式:Φ=BS。
(3)单位:1 Wb=1_T·m2。
(4)物理意义:相当于穿过某一面积的磁感线的条数。
2.电磁感应现象
(1)电磁感应现象
当穿过闭合电路的磁通量发生变化时,电路中有感应电流产生的现象。
(2)产生感应电流的条件
①条件:穿过闭合电路的磁通量发生变化。
②特【典例】闭合电路的一部分导体在磁场内做切割磁感线的运动。
(3)产生电磁感应现象的实质
电磁感应现象的实质是产生感应电动势,如果回路闭合则产生感应电流;如果回路不闭合,则只产生感应电动势,而不产生感应电流。
(4)能量转化
发生电磁感应现象时,机械能或其他形式的能转化为电能。
二、楞次定律
1.楞次定律
(1)内容:感应电流的磁场总要阻碍引起感应电流的磁通量的变化。
(2)适用范围:适用于一切回路磁通量变化的情况。
(3)楞次定律中“阻碍”的含义
2.右手定则
(1)内容
①磁感线穿入右手手心。
②大拇指指向导体运动的方向。
③其余四指指向感应电流的方向。
(2)适用范围:适用于部分导体切割磁感线。
三、 法拉第电磁感应定律的理解和应用
1.感应电动势
(1)概念:在电磁感应现象中产生的电动势。
(2)产生条件:穿过回路的磁通量发生改变,与电路是否闭合无关。
(3)方向判断:感应电动势的方向用楞次定律或右手定则判断。
2.法拉第电磁感应定律
(1)内容:感应电动势的大小跟穿过这一电路的磁通量的变化率成正比。
(2)公式:E=n,其中n为线圈匝数。
(3)感应电流与感应电动势的关系:遵守闭合电路欧姆定律,即I=。
3.磁通量变化通常有三种方式
(1)磁感应强度B不变,垂直于磁场的回路面积发生变化,此时E=nB;
(2)垂直于磁场的回路面积不变,磁感应强度发生变化,此时E=nS,其中是B-t图象的斜率。
(3)磁通量的变化是由于面积和磁场变化共同引起的,则根据定义求,ΔΦ=Φ末-Φ初,E=n≠n。
在图象问题中磁通量的变化率是Φ-t图象上某点切线的斜率。
四、 导体切割磁感线产生感应电动势的计算
1.公式E=Blv的“四性”
(1)正交性:本公式是在一定条件下得出的,除磁场为匀强磁场外,还需B、l、v
三者互相垂直。
(2)瞬时性:若v为瞬时速度,则E为相应的瞬时感应电动势。
(3)有效性:公式中的l为导体切割磁感线的有效长度。
如图中,棒的有效长度为a、b间的距离。
(4)相对性:E=Blv中的速度v是导体相对磁场的速度,若磁场也在运动,应注意速度间的相对关系。
2.导体在磁场中旋转产生的感应电动势
导体棒绕一端在匀强磁场中转动切割磁感线产生的感应电动势为E=Bωl2。
五、自感现象 涡流
1.自感现象:由于通过导体自身的电流发生变化而产生的电磁感应现象。
2.自感电动势:
(1)定义:在自感现象中产生的感应电动势。
(2)表达式:E=L。
(3)自感系数L。
①相关因素:与线圈的大小、形状、圈数以及是否有铁芯等因素有关。
②单位:亨利(H),常用单位还有毫亨(mH)、微亨(μH)。1 mH=10-3 H,1 μH=10-6 H。
3.自感中灯泡“闪亮”与“不闪亮”的原因
与线圈串联的灯泡
与线圈并联的灯泡
电路图
通电时
电流逐渐增大,灯泡逐渐变亮
电流突然增大,然后逐渐减小达到稳定
断电时
电流逐渐减小,灯泡逐渐变暗,电流方向不变
电路中稳态电流为I1、I2:①若I2≤I1,灯泡逐渐变暗;②若I2>I1,灯泡闪亮后逐渐变暗。两种情况灯泡中电流方向均改变
4.涡流:当线圈中的电流发生变化时,在它附近的导体中产生的像水的旋涡一样的感应电流。
(1)电磁阻尼:当导体在磁场中运动时,感应电流会使导体受到安培力,安培力的方向总是阻碍导体的相对运动。
(2)电磁驱动:如果磁场相对于导体转动,在导体中产生的感应电流使导体受到安培力的作用而运动起来。
(3)电磁阻尼和电磁驱动的原理体现了楞次定律的推广应用。
【查漏补缺】
一、电磁感应现象的判断
判断电磁感应现象是否发生的一般思路
(1)明确研究的是哪条闭合回路;
(2)理清该闭合回路内的磁场分布情况,并确定该回路中磁通量是否变化。
①若磁通量发生变化,则回路中有感应电流。
②若磁通量没有发生变化,则回路中无感应电流
【典例】如图所示 ,通有恒定电流的导线MN与闭合金属框共面,第一次将金属框由Ⅰ平移到Ⅱ,第二次将金属框绕cd边翻转到Ⅱ,设先后两次通过金属框的磁通量变化量大小分别为ΔΦ1和ΔΦ2,则( )
A.ΔΦ1>ΔΦ2,两次运动中线框中均有沿adcba方向电流出现
B.ΔΦ1=ΔΦ2,两次运动中线框中均有沿abcda方向电流出现
C.ΔΦ1<ΔΦ2,两次运动中线框中均有沿adcba方向电流出现
D.ΔΦ1<ΔΦ2,两次运动中线框中均有沿abcda方向电流出现
【答案】 C
二、楞次定律的理解应用
对楞次定律中“阻碍”的含义可以推广为感应电流的效果总是阻碍产生感应电流的原因:
(1)阻碍原磁通量的变化——“增反减同”;
(2)阻碍相对运动——“来拒去留”;
(3)使线圈面积有扩大或缩小的趋势——“增缩减扩”;
(4)阻碍原电流的变化(自感现象)——“增反减同”。
【典例】(多选)(2014·上海卷)如图,匀强磁场垂直于软导线回路平面,由于磁场发生变化,回路变为圆形。则该磁场( )
A.逐渐增强,方向向外
B.逐渐增强,方向向里
C.逐渐减弱,方向向外
D.逐渐减弱,方向向里
【答案】 CD
三、 法拉第电磁感应定律的理解和应用
1.应用法拉第电磁感应定律解题的一般步骤
(1)分析穿过闭合电路的磁场方向及磁通量的变化情况;
(2)利用楞次定律确定感应电流的方向;
(3)灵活选择法拉第电磁感应定律的不同表达形式列方程求解。
2.应注意的问题
通过回路的电荷量q仅与n、ΔΦ和回路电阻R有关,与变化过程所用的时间长短无关,推导过程:q=Δt=Δt=
【典例】如图所示,匀强磁场中有一矩形闭合线圈abcd,线圈平面与磁场垂直。已知线圈的匝数N=100,边长ab=1.0 m、bc=0.5 m,电阻r=2 Ω。磁感应强度B在0~1 s内从零均匀变化到0.2 T。在1~5 s内从0.2 T均匀变化到-0.2 T,取垂直纸面向里为磁场的正方向。求:
(1)0.5 s时线圈内感应电动势的大小E和感应电流的方向;
(2)在1~5 s内通过线圈的电荷量q;
(3)在0~5 s内线圈产生的焦耳热Q。
【答案】 (1)10 V,感应电流的方向为a→d→c→b→a (2)10 C (3)100 J
(2)同理可得E2=N,感应电流I2=
电荷量q=I2Δt2,解得q=N,代入数据得q=10 C。
(3)0~1 s内的焦耳热Q1=IrΔt1,且I1=,1~5 s内的焦耳热Q2=IrΔt2
由Q=Q1+Q2,代入数据得Q=100 J。
四、电磁感应中的“杆+导轨”模型
1.模型特点
“杆+导轨”模型是电磁感应问题高考命题的“基本道具”,也是高考的热点。
“杆+导轨”模型问题的物理情境变化空间大,涉及的知识点多。
2.分析思路
【典例】(2015·海南单科·13)如图,两平行金属导轨位于同一水平面上,相距l,左端与一电阻R相连;整个系统置于匀强磁场中,磁感应强度大小为B,方向竖直向下。一质量为m的导体棒置于导轨上,在水平外力作用下沿导轨以速率v匀速向右滑动,滑动过程中始终保持与导轨垂直并接触良好。已知导体棒与导轨间的动摩擦因数为μ,重力加速度大小为g,导轨和导体棒的电阻均可忽略。求:
(1)电阻R消耗的功率;
(2)水平外力的大小。
【答案】 (1) (2)+μmg
五、电磁感应中的图象问题
1.图象类型
图象类型
(1)随时间变化的图象如B-t图象、Φ-t图象、E-t图象、I-t图象和F-t图象
(2)随位移x变化的图象如E-x图象和I-x图象
问题类型
(1)由给定的电磁感应过程选择图象或画出图象
(2)由给定的有关图象分析电磁感应过程,求解相应的物理量
应用知识
左手定则、安培定则、右手定则、楞次定律、法拉第电磁感应定律、欧姆定律、牛顿定律、函数图象知识等
2.突破策略
对图象的分析,应做到“四明确一理解”,即:
(1)明确图象所描述的物理意义;明确各种“+”、“-”的含义;明确斜率的含义;明确图象和电磁感应过程之间的对应关系。
(2)理解三个相似关系及各自的物理意义:
v~Δv~,B~ΔB~,Φ~ΔΦ~。
3.解决图象问题的一般步骤
(1)明确图象的种类,即是B-t图象还是Φ-t图象,或者E-t图象、I-t图象等。
(2)分析电磁感应的具体过程。
(3)用右手定则或楞次定律确定方向对应关系。
(4)结合法拉第电磁感应定律、欧姆定律、牛顿定律等规律写出函数关系式。
(5)根据函数关系式,进行数学分析,如分析斜率的变化、截距等。
(6)判断图象或图象分析相关问题。
【典例】
如图所示,一直角三角形金属框,向左匀速地穿过一个方向垂直于纸面向内的匀强磁场区域,磁场仅限于虚线边界所围的区域,该区域的形状与金属框完全相同,且金属框的下边与磁场区域的下边在一直线上。若取顺时针方向为电流的正方向,则金属框穿过磁场的过程中感应电流i随时间t变化的图象是( )
【答案】 C
方向为顺时针方向,金属框切割磁感线的有效长度线性减小,排除D,故C正确。
六、电磁感应中的电路问题
1.电磁感应中物理量的关系图
2.处理电磁感应电路问题的一般思路:
【典例】(多选)如图所示,PN与QM两平行金属导轨相距1 m,电阻不计,两端分别接有电阻R1和R2,且R1=6 Ω,ab杆的电阻为2
Ω,在导轨上可无摩擦地滑动,垂直穿过导轨平面的匀强磁场的磁感应强度为1 T。现ab以恒定速度v=3 m/s匀速向右移动,这时ab杆上消耗的电功率与R1、R2消耗的电功率之和相等。则( )
A.R2=6 Ω
B.R1上消耗的电功率为0.375 W
C.a、b间电压为3 V
D.拉ab杆水平向右的拉力为0.75 N
【答案】 BD
【解析】
七、电磁感应中的动力学问题
1.导体的两种运动状态
(1)平衡状态:静止或匀速直线运动,F合=0。
(2)非平衡状态:加速度不为零,F合=ma。
2.电学对象与力学对象的转换及关系
【典例】如图甲所示,相距L=20 cm的平行、光滑金属导轨倾斜放置,处于垂直导轨平面向上的匀强磁场中,磁感应强度B= T。上端通过电键S与电阻R相连,R=10 Ω。某金属棒质量m=20 g,垂直导轨放置且接触良好。现断开电键S,由静止释放金属棒,过一段时间后再突然闭合电键S。图乙所示为金属棒开始运动到闭合电键前的v-t图象。导轨和金属棒的电阻不计,导轨足够长。(g=10 m/s2)
(1)求闭合电键后,金属棒的稳定速度为多大?
(2)若从释放金属棒开始金属棒下滑了25 m达到稳定速度,则这段时间内通过金属棒的电荷量为多少?电路中产生的内能是多少?
【答案】 (1)10 m/s (2)0.45 C 2 J
(2)由题图可知,闭合电键前,金属棒运动位移x1=t1=12 m
闭合电键后金属棒达到稳定速度,金属棒位移x2=13 m
=
=
q=t2
解得q=0.45 C
由能量守恒得:mgxsin θ=Q+mv′2
解得Q=2 J。
八、电磁感应中的能量问题
1.能量转化过程
(1)导体切割磁感线或磁通量发生变化产生感应电流的过程就是机械能或其他形式的能转化成电能的过程。
(2)克服安培力做的功等于转化的电能,纯电阻电路中,电能以内能形式消耗。
2.选用解题规律
(1)动能定理:合外力(包含安培力)所做的功等于导体棒动能的增量。
(2)能量转化和守恒定律:
①判断选定的系统在某一过程中能量是否守恒。
②分析该过程中能量形式,哪种能量增加,哪种能量减少。
③增加的能量等于减少的能量。
3.求解电磁感应回路焦耳热Q的几种方法
【典例】(2015·天津理综·11)如图所示,“凸”字形硬质金属线框质量为m,相邻各边互相垂直,且处于同一竖直平面内,ab边长为l,cd边长为2l,ab与cd平行,间距为2l。匀强磁场区域的上下边界均水平,磁场方向垂直于线框所在平面。开始时,cd边到磁场上边界的距离为2l,线框由静止释放,从cd边进入磁场直到ef,pq边进入磁场前,线框做匀速运动,在ef、pq边离开磁场后,ab边离开磁场之前,线框又做匀速运动。线框完全穿过磁场过程中产生的热量为Q。线框在下落过程中始终处于原竖直平面内,且ab、cd边保持水平,重力加速度为g。求:
(1)线框ab边将离开磁场时做匀速运动的速度大小是cd边刚进入磁场时的几倍;
(2)磁场上下边界间的距离H。
【答案】 (1)4倍 (2)+28l
【解析】 (1)设磁场的磁感应强度大小为B,cd边刚进入磁场时,线框做匀速运动的速度为v1,cd边上的感应电动势为E1,由法拉第电磁感应定律,有E1=2Blv1①
设线框总电阻为R,此时线框中电流为I1,由闭合电路欧姆定律,有I1=②
设此时线框所受安培力为F1,有F1=2I1lB③
由于线框做匀速运动,其受力平衡,有mg=F1④
由①②③④式得v1=⑤
设ab边离开磁场之前,线框做匀速运动的速度为v2,同理可得v2=⑥
由⑤⑥式得v2=4v1⑦