高中物理竞赛复赛模拟试题一 8页

1 / 8 高中物理竞赛复赛模拟卷（一） 姓名 分数 (本试卷与模拟试卷沈晨卷相同 ) 1．（20 分） 设想宇宙中有 1 个由质量分别为 m 1、m2⋯⋯m N 的星体 1、2⋯⋯N 构成的孤立星团，各星体空间 位置间距离均为 a，系统总质量为 M ，由于万有引力的作用， N 个星体将同时由静止开始运动。试问经过多 长时间各星体将会相遇？ 2．（25 分）（ 1）在两端开口的竖直放置的 U 型管中注入水银，水银柱的全长为 h。若把管的右端封闭，被封 闭的空气柱长 L，然后使水银柱作微小的振荡，设空气为理想气体，且认为水银振荡时右管内封闭气体经历 的是准静态绝热过程， 大气压强相当于 h0 水银柱产生的压强， 空气的绝热指数为 。试求水银振动的周期 T2。 已知对于理想气体的绝热过程有 PV =常数。 （2）在大气压下用电流加热 1 个绝热金属片，使其以恒定的功率 P 获取电热，发现在一定的温度范围内金属 绝对温度 T 随时间 t 的增长关系为 4/1 00 )](1[)( ttaTtT 。其中 T0、a、t0 均为常量。求该金属片的热容量 CP 随温度 T 变化的关系。 3．（20 分） 如图所示，当船舶抛锚时，要把缆绳在系锚桩上绕好几圈（ N 圈），这样做时，锚桩抓住缆绳必须 的力，经船作用于缆绳的力小得多，以避免在船舶遭到突然冲击时拉断缆绳，这两力比 F1:F2，与缆绳绕系锚 桩的圈数有关，设泊船时将缆绳在系锚桩上绕了 5 圈，计算比值 F1:F2 ， 设 缆绳与锚桩间的摩擦因数 2.0 。 4．（25 分） 速调管用于甚高频信号的放大，速调管主要由两个相距为 b 的腔组成，每个腔有 1 对平行板，如 图所示，初始速度为 v0 的一束电子通过板上的小孔横穿整个系统。要放大的高频信号以一定的相位差（ 1 个 周期对应于 2π相位）分别加在两对电极板上，从而在每个腔中产生交变水平电场。当输入腔中的电场方向向 右时，进入腔中的电子被减速；反之，电场方向向左时，电子被加速。这样，从输入腔中射出的电子经过一 定的距离后将叠加成短电子束。如果输出腔位于该电子束形成处，那么，只要加于其上的电压相位选择恰当。 输出腔中的电场将从电子束中吸收能量。设电压信号为周期 T=1.0×10 －9s，电压 U=0.5V 的方波。电子束的初 始速度 v0=2.0 ×106m/s，电子荷质比 e/m=1.76 ×1011C/kg 。假定间距 a 很小，电子渡越腔的时间可忽略不计。保 留 4 位有效数字。计算： （1）使电子能叠加成短电子束的距离 b。（2）由相移器提供的所需的输出腔也输入 腔之间的相位差。 2 / 8 5．（25 分） 如图所示，为一个英国作家提出的一个登天缆绳的设想：用一根足够长的缆绳，竖在赤道上空， 这根绳不会飞离地球，因此可以通过这根缆绳向地球卫星运送物品，甚至沿绳爬到太空去游览。科学家认为 这个设想是合理的，但这种缆绳的抗拉力长度（即这样长度的绳子将被自身重力所拉断）极大。 （1）根据力学原理，给出这根缆绳上任一位置 r 处绳的张力，并确定张力最大的位置。 （2）取地球半径 R=6400km ，地球同步卫星轨道半径 r0=6.6R，估算这种缆绳的抗拉力长度 L。 （3）估算这条登天缆绳的长度 L0。 6．（25 分） 如图所示，电路由下列元器件组成：开始时未充电、电容值为 C 的电容器，电感为 L、电阻为零 的线圈，电动势为 ε、内阻忽略的电池，以及氖灯 N 和开关 S。氖灯在其接点电压小于燃点电压 U z 时保持绝 缘体的特性，而超过这个电压时即点燃，并引起电容器迅速放电，至被称为熄灭电压的电压值 Ug，以后电流 就又停止。假定电容器通过氖灯放电的时间非常短， 可以认为放电过程中流过线圈的电流没有变化。 在 ε=34V， Uz=64V ，Ug=22V 时，闭合 S 后氖灯共亮几次？电容器上电压在什么区间变化？ 提示：利用力与电的相似 比拟。 高中物理竞赛复赛模拟卷（一）答案与分析 第一题（ 20 分） 3 / 8 解析：设系统的质心为 O，可先研究质量为 m1 的质点 1，它将受到其它各质点的引力： )( 123 2121 rr a mGmF ； 1 3 31 3 13 ( )Gm mF r r a ur r r ⋯⋯ 1 1 13 ( )N N N GmmF r r a ur r r 上列各式中， ),2,1( Nir i 为各质点对质心 O 位置的矢径。则质点 1 所受合力 为 ])([ 12122113 1 1 rmmmrmrmrm a GmF NNN 由于 O 为质心，系统不受外力，故 011 rm ， 则有 13 11213 11 ])([ r a MGmrmmm a GmF N 。若设矢量 1r 的大小为 kar1 ，那么质点 1 所 受其它质点引力的合力大小为 2 1 3 1 3 1 1 r MkGmka a MGmF 质点 1 所受各质点引力的合力等效于质量为 Mk3 的质点对它发生的引力， 1 在这个平方反比作用下，在 以 O 为 1 个焦点，以 r/2 为长半轴，而短半轴为零的 “椭圆轨道 ”运动，初始位置为 “远地点 ”，经半个周期，到 达“近地点 ”O。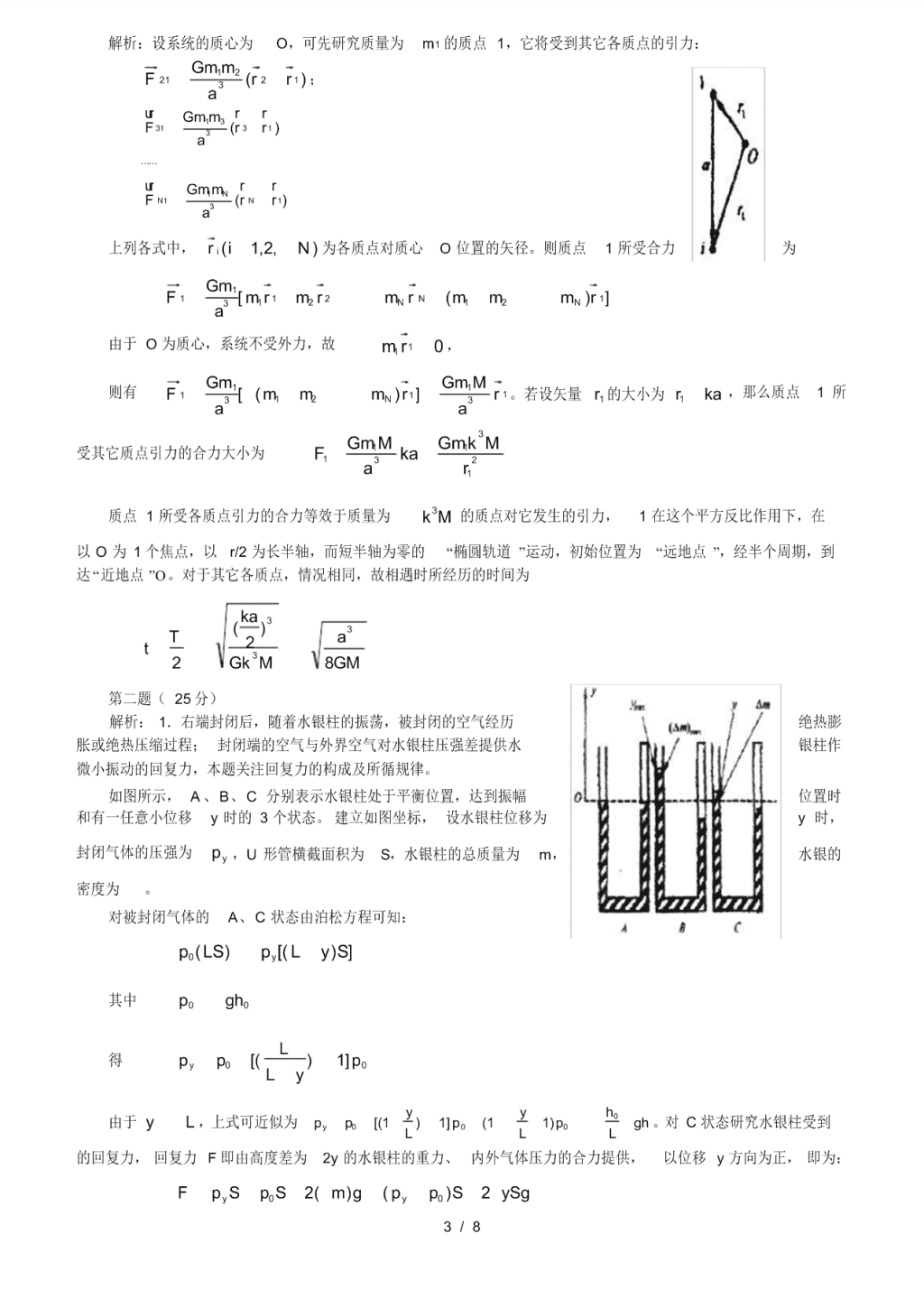对于其它各质点，情况相同，故相遇时所经历的时间为 GM a MGk ka Tt 8 ) 2 ( 2 3 3 3 第二题（ 25 分） 解析： 1．右端封闭后，随着水银柱的振荡，被封闭的空气经历 绝热膨 胀或绝热压缩过程； 封闭端的空气与外界空气对水银柱压强差提供水 银柱作 微小振动的回复力，本题关注回复力的构成及所循规律。 如图所示， A 、B、C 分别表示水银柱处于平衡位置，达到振幅 位置时 和有一任意小位移 y 时的 3 个状态。 建立如图坐标， 设水银柱位移为 y 时， 封闭气体的压强为 yp ，U 形管横截面积为 S，水银柱的总质量为 m， 水银的 密度为 。 对被封闭气体的 A、C 状态由泊松方程可知： ])[()(0 SyLpLSp y 其中 00 ghp 得 00 ]1)[( p yL Lpp y 由于 Ly ，上式可近似为 0 0 0 0[(1 ) 1] (1 1)y hy yp p p p ghL L L 。对 C 状态研究水银柱受到 的回复力， 回复力 F 即由高度差为 2y 的水银柱的重力、 内外气体压力的合力提供， 以位移 y 方向为正， 即为： ySgSppgmSpSpF yy 2)()(2 00 4 / 8 ysggs L h ysggys L h )2( 2 0 0 令 sggs L hk 20 得 kyF ，可知水银柱的微小振荡为一简谐运动，其周期为： g L h h sggs L h hs k mT )2( 2 2 22 00 2 解析： 2．由热容量定义 T tPC p ，而 1 1 4 4 0 0 0 0[1 ( ) ] [1 ( ) ]T a t t t T a t tT t t 1 3 1 4 4 4 0 0 0 0 3 0 4 0 30 0 1{[1 ( )] [1 ( )] [1 ( )] }4 [1 ( )] 4 [ ] 4 T a t t a t t a t a t t t T a a t t T a T T 故 3 3 0 4 T aT PC p 第三题（ 20 分） 解析： 从整体分析来看， 缆绳一端较大的力 F1 由另一端锚桩抓住缆绳的力 F2 及锚桩对绳的摩擦力来平衡， 多绕几圈增加缆绳与锚桩的接触而累积起更大的摩擦力。但由于在绳子与锚桩接触的各处正压力不同，故摩 擦力亦不相同。这就需要考察某一微元绳段的受力情况，而后广及全绳。 如图所示，首先将锚桩视作圆柱，每一圈绳为一圆周，对整个缆绳作无限均匀分割，使每段绳元所对圆 心角为 n n N ,2 。取任意第 i 段绳元作受力分析：两端其它绳 的 拉 力 iT 、 1iT ，静摩擦力 if ，锚桩的支持力 iN ，当缆绳恰处平衡时有下列关 系： 2 sin)( 2 cos)( 11 iiiii TTNTT 取 iii TTT 21 ，上式为 2 tan21 i ii T TT ，即 n N T T i i 211 ① 这就是说，绳上张力是等比递增的，现对①式两边同时取 n 次方，有 nn i i n N T T )21()( 1 上式两边取极限有 5 / 8 N N N n N n e n N F F 2 2 2 2 1 2 )21(lim 。代入题给数据可得 535 1 2 F F 第四题（ 25 分） 解析： 1．电子通过输入腔时被加速或减速。由 2 0 2 1 2 1 2 1 mvmvUe 得 )2(2 01 m Uevv ；要形成短电 子束，应使后半周期通过输入腔被加速的电子经过一段距离 b 在输出腔 “追 ”上前半周期通过入腔被减速的电 子，从而叠加成短电子束，故此应有： )2(2)2( 2 0 2 0 m Uev bT m Uev b 即 2)2()2( )2( 2 0 2 0 24 0 T m Uev m Uev m Uev b = m69 10 956.1044.2 044.2956.110 2 0.1 .10272.2 2m 2．为使电场从短电子束中吸收能量，应使电场方向向右，对进入电场的电子做负功，使电子释放动能。 当输入腔电场方向向右时满足 2 0 2 2 , 2 b k UeT v m 则 2 22 0 k m UevT b 2 100.110956.1 10272.2 96 2 k = .2)62.11( k 223262.0 或 137228.0 第五题（ 25 分） 解析：设定地球自转角速度为 ，地球质量为 M ，绕地球运动轨道高度为 r，同 步轨道高度为 0r ，缆绳线密度为 ，长 L。如图所示，取缆绳上距地心 r 的某微元 n n Rr n Lr , ，其质量 .rm 绳元之所以在该高度相对地球静止， 6 / 8 是因其受力 —— 上、下端绳的张力差 iT 与地心引力满足下列关系 .2 2 rmT r mGM i GM r r rGMTi 2 2 1 ① 由于 ,3 0 2 2 g r R 而 gRGM 2 ，则①式为 3 0 2 2 1 r r rgrRTi = 3 0 2 2 )( )( 1 r riR riR grR ② 由②式可知， 00 iT，rr 时 ，绳元上端张力大于下端张力，说明在同步轨道高度以下，缆绳上张力 随 r 增大而增大； 00 iT，rr 时 ，说明在同步轨道高度以上，缆绳上张力随 r 增大而减小；可见当 0,0 iTrr ，即处于同步轨道高度处绳的张力最大。下面用数学方法求出此最大值： 2 2 31 0 1 ( ) lim ( ) n n i R i rT rR g R i r r n in r riRr riRriR rgR 1 3 0 2 )( ))()1((lim = rRrRrRrRR gR n 2 1 2 1111 lim2 )321(1 3 0 2 3 0 n r r r Rr rnR = 3 0 2 3 0 2 2 11 r L r LR LRR gR = 3 0 2 3 0 2 2 2 )(11 r Rr r RrR rR gR = 3 0 2 3 0 2 2 2 1 2 1 r r rr R R gR 上式中括号内减数项为 3 0 2 22 1 2 1 r r rr ，注意 3 项积 3 0 2 22 1 2 1 r r rr 为定值，则当 0rr 时，减数项有最 小值，张力有最大值 maxT ， 2 2 2 0 max 3 0 31 2 R rT gR R r 7 / 8 在同步轨道处缆绳张力最大，抗拉力长度指重力与最大张力相当的缆绳之长，以题给数据估算： .4957 )64006.6(2 )64006.6(36400 6400 16400 3 22 2 kmLggd 最后，缆绳总长只须求 T=0 处的 r： 0 2 1 2 1 3 0 2 3 0 2 r r rr R R 3 02)( rrRRr 31 1 4 2 6.6 2r R 可得总长 4 0 15 10 .L km 第六题（ 25 分） 先将含有恒定电动势 的 LC 电磁振荡与含有恒定重力的弹簧振子谐振相比拟： 对于弹簧振子可给出其合力随时间变化的规律： sinF mg KA t ，于是可知在 LC 电路中，电容器上 电压变化规律为 sin .c Cu t C 据此， 当 17 15sin,sin343464 1 00 LCtLCt 时， 氖灯点燃， 电容器放电。 电压突然减至 22V 时，使氖灯重新熄灭。回路又重新作谐振，周期不变，电流也不因放电改变。现在从能量角度确定放电后电 容器可达到的最大电压 mu 为： 对比于弹簧振子振动能 22 2 1 2 1 kxmv 定值，对 LC 电磁振荡系统，放电前系统能量守恒，有 2 2 2 1 1 1 1 1 ( ) ; 2 2 2z zL I Cu C C C C 放电后系统能量守恒，有 2 2 2 1 1 1 1 1 ; 2 2 2z g mL I Cu C Cu C C C 8 / 8 则有 222 2 2 )()()( gm uuuE ，于是可得 Vuuu gm )2034()()( 22 2 2 ，即放电后电容器上电压在 14V ～54V 之间振荡， 可见氖灯只亮 1 次。