2020届二轮复习气体实验定律理想气体状态方程课件（38张） 38页

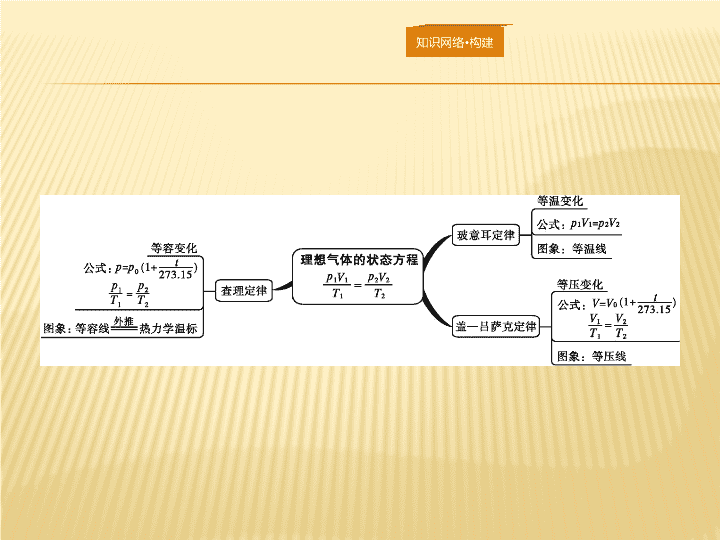
气体实验定律、理想气体状态方程 1 2 3 4 5 1 . (2019 全国卷 Ⅰ ) 热等静压设备广泛应用于材料加工中。该设备工作时 , 先在室温下把惰性气体用压缩机压入到一个预抽真空的炉腔中 , 然后炉腔升温 , 利用高温高气压环境对放入炉腔中的材料加工处理 , 改善其性能。一台热等静压设备的炉腔中某次放入固体材料后剩余的容积为 0 . 13 m 3 , 炉腔抽真空后 , 在室温下用压缩机将 10 瓶氩气压入到炉腔中。已知每瓶氩气的容积为 3 . 2 × 10 - 2 m 3 , 使用前瓶中气体压强为 1 . 5 × 10 7 Pa, 使用后瓶中剩余气体压强为 2 . 0 × 10 6 Pa; 室温温度为 27 ℃ 。氩气可视为理想气体。 (1) 求压入氩气后炉腔中气体在室温下的压强 ; (2) 将压入氩气后的炉腔加热到 1 227 ℃ , 求此时炉腔中气体的压强。 1 2 3 4 5 解析 : (1) 设初始时每瓶气体的体积为 V 0 , 压强为 p 0 ; 使用后气瓶中剩余气体的压强为 p 1 。假设体积为 V 0 、压强为 p 0 的气体压强变为 p 1 时 , 其体积膨胀为 V 1 。由玻意耳定律 p 0 V 0 =p 1 V 1 ① 被压入炉腔的气体在室温和 p 1 条件下的体积为 V 1 '=V 1 -V 0 ② 设 10 瓶气体压入完成后炉腔中气体的压强为 p 2 , 体积为 V 2 。由玻意耳定律 p 2 V 2 = 10 p 1 V 1 ' ③ 联立 ①②③ 式并代入题给数据得 p 2 = 3 . 2 × 10 7 Pa ④ (2) 设加热前炉腔的温度为 T 0 , 加热后炉腔温度为 T 1 , 气体压强为 p 3 。 联立 ④⑤ 式并代入题给数据得 p 3 = 1 . 6 × 10 8 Pa ⑥ 答案 : (1)3 . 2 × 10 7 Pa 　 (2)1 . 6 × 10 8 Pa 1 2 3 4 5 2 . (2019 全国卷 Ⅱ ) 如图 , 一容器由横截面积分别为 2 S 和 S 的两个汽缸连通而成 , 容器平放在水平地面上 , 汽缸内壁光滑。整个容器被通过刚性杆连接的两活塞分隔成三部分 , 分别充有氢气、空气和氮气。平衡时 , 氮气的压强和体积分别为 p 0 和 V 0 , 氢气的体积为 2 V 0 , 空气的压强为 p 。现缓慢地将中部的空气全部抽出 , 抽气过程中氢气和氮气的温度保持不变 , 活塞没有到达两汽缸的连接处 , 求 (1) 抽气前氢气的压强 ; (2) 抽气后氢气的压强和体积。 1 2 3 4 5 解析 : (1) 设抽气前氢气的压强为 p 10 , 根据力的平衡条件得 ( p 10 -p )·2 S= ( p 0 -p )· S ① 得 p 10 = ( p 0 +p ) ② (2) 设抽气后氢气的压强和体积分别为 p 1 和 V 1 , 氮气的压强和体积分别为 p 2 和 V 2 。 根据力的平衡条件有 p 2 · S=p 1 ·2 S ③ 由玻意耳定律得 p 1 V 1 =p 10 ·2 V 0 ④ p 2 V 2 =p 0 V 0 ⑤ 由于两活塞用刚性杆连接 , 故 V 1 - 2 V 0 = 2( V 0 -V 2 ) ⑥ 1 2 3 4 5 3 . (2019 全国卷 Ⅲ ) 如图 , 一粗细均匀的细管开口向上竖直放置 , 管内有一段高度为 2 . 0 cm 的水银柱 , 水银柱下密封了一定量的理想气体 , 水银柱上表面到管口的距离为 2 . 0 cm 。若将细管倒置 , 水银柱下表面恰好位于管口处 , 且无水银滴落 , 管内气体温度与环境温度相同。已知大气压强为 76 cmHg, 环境温度为 296 K 。 (1) 求细管的长度 ; (2) 若在倒置前 , 缓慢加热管内被密封的气体 , 直到水银柱的上表面恰好与管口平齐为止 , 求此时密封气体的温度。 1 2 3 4 5 解析 : (1) 设细管的长度为 L , 横截面的面积为 S , 水银柱高度为 h ; 初始时 , 设水银柱上表面到管口的距离为 h 1 , 被密封气体的体积为 V , 压强为 p ; 细管倒置时 , 气体体积为 V 1 , 压强为 p 1 。由玻意耳定律有 pV=p 1 V 1 ① 由力的平衡条件有 p=p 0 + ρ gh ② p 1 =p 0 - ρ gh ③ 式中 , ρ 、 g 分别为水银的密度和重力加速度的大小 , p 0 为大气压强。由题意有 V=S ( L-h 1 -h ) ④ V 1 =S ( L-h ) ⑤ 由 ①②③④⑤ 式和题给数据得 L= 41 cm ⑥ 1 2 3 4 5 (2) 设气体被加热前后的温度分别为 T 0 和 T , 由盖 - 吕萨克定律有 由 ④⑤⑥⑦ 式和题给数据得 T= 312 K 。 ⑧ 答案 : (1)41 cm 　 (2)312 K 1 2 3 4 5 4 . (2018 全国卷 Ⅰ ) 如图 , 容积为 V 的汽缸由导热材料制成 , 面积为 S 的活塞将汽缸分成容积相等的上下两部分 , 汽缸上部通过细管与装有某种液体的容器相连 , 细管上有一阀门 K 。开始时 ,K 关闭 , 汽缸内上下两部分气体的压强均为 p 0 。现将 K 打开 , 容器内的液体缓慢地流入汽缸 , 当流入的液体体积为 时 , 将 K 关闭 , 活塞平衡时其下方气体的体积减小了 。不计活塞的质量和体积 , 外界温度保持不变 , 重力加速度大小为 g 。求流入汽缸内液体的质量。 1 2 3 4 5 1 2 3 4 5 5 . (2018 全国卷 Ⅱ ) 如图 , 一竖直放置的汽缸上端开口 , 汽缸壁内有卡口 a 和 b , a 、 b 间距为 h , a 距缸底的高度为 H ; 活塞只能在 a 、 b 间移动 , 其下方密封有一定质量的理想气体。已知活塞 质量为 m , 面积为 S , 厚度可忽略 ; 活塞和汽缸壁均绝热 , 不计它们之间的摩擦 , 开始时活塞处于静止状态 , 上、下方气体压强均为 p 0 , 温度均为 T 0 。现用电热丝缓慢加热汽缸中的气体 , 直至活塞刚好到达 b 处 , 求此时汽缸内气体的温度以及在此过程中气体对外所做的功。重力加速度大小为 g 。 1 2 3 4 5 考点 1 考点 2 考点 3 “ 玻璃管液封 ” 模型 例 1 (2019 吉林三调 ) 如图所示 , 竖直放置的 U 形管左端封闭 , 右端开口 , 左管横截面积为右管横截面积的 2 倍 , 在左管内用水银封闭一段长为 l 、温度为 T 的空气柱 , 左右两管水银面高度差为 h cm, 外界大气压为 h 0 cmHg 。 (1) 若向右管中缓慢注入水银 , 直至两管水银面相平 ( 原右管中水银没全部进入水平部分 ), 求在右管中注入水银柱的长度 h 1 ( 以 cm 为单位 ); (2) 在两管水银面相平后 , 缓慢升高气体的温度至空气柱的长度为开始时的长度 l , 求此时空气柱的温度 T' 。 考点 1 考点 2 考点 3 解题思路 (1) 以封闭气体为研究对象 , 先结合连通器的原理求出初末状态的压强 , 应用玻意耳定律可以求出气体的长度 , 再由几何关系即可求出 h 1 ; (2) 水银总质量一定时 , 在液面上升或下降的过程中 , 水银的体积保持不变 ; 根据题意求出封闭气体的压强 , 然后应用理想气体的状态方程求出气体的温度。 考点 1 考点 2 考点 3 解析 : (1) 注入水银过程封闭气体等温变化 , 初状态 : p 1 = ( h 0 -h ) cmHg, V 1 =lS , 末状态 : p 2 =h 0 cmHg, V 2 =l'S 由玻意耳定律 : p 1 V 1 =p 2 V 2 ① 在左侧的试管中 , 液面上升的高度 :Δ h=l-l' 进入左侧试管中的水银的体积 :Δ V= Δ h · S 所以注入右侧的水银的体积 :Δ V 0 = ( h+ Δ h ) S 2 + Δ V= ( h+ 3Δ h ) S 2 所以在右管中注入水银柱的长度 考点 1 考点 2 考点 3 考点 1 考点 2 考点 3 方法归纳 液柱封闭气体问题的研究方法 求液柱封闭的气体压强时 , 一般以液柱为研究对象分析受力、列平衡方程。 (1) 液体因重力产生的压强大小为 p= ρ gh ( 其中 h 为气体至液面的竖直高度 ); (2) 不要漏掉大气压强 , 同时又要尽可能平衡掉某些大气的压力 ; (3) 有时可直接应用连通器原理 —— 连通器内静止的液体 , 同种液体在同一水平面上各处压强相等 ; (4) 当液体为水银时 , 可灵活应用压强单位 “cmHg”, 使计算过程简捷。 考点 1 考点 2 考点 3 对应训练 1 . (2019 山西二模 ) 如图 , 粗细均匀的等臂 U 形管竖直放置 , 其左管封闭有一定量的气体 , 右管开口与大气相通 , 左右两侧被水银柱隔开。平衡时测得左管内气柱的长度为 l , 右管内水银面高于左管内水银面 h 。现从右管开口处用一不计厚度的活塞缓慢向下压气体 , 已知活塞与管密封良好 , 水银的密度为 ρ , 大气压强为 p 0 , 重力加速度为 g 。若整个过程中气体温度保持不变 , 求活塞压下多少距离时左右两管水银面相齐平。 考点 1 考点 2 考点 3 考点 1 考点 2 考点 3 2 . (2019 安徽黄山二模 ) 如图所示 , 粗细均匀的 U 形玻璃管 , 竖直放置 , 左端开口 , 右端封闭。一定质量的理想气体 B , 气柱长为 L= 12 . 5 cm, 左端长为 h= 4 cm 的水银柱封闭了一定质量的理想气体 A , 气柱长度也为 h , 且两端最上方液面齐平。现再往左端缓慢加入长为 h 的水银柱。已知大气压强为 p 0 = 76 cmHg, 整个过程温度保持不变。当气柱稳定时 , 求 : 右端液面上升的高度 L 0 及气柱 A 的长度 L A ( 计算结果均保留一位小数 ) 。 考点 1 考点 2 考点 3 解析 : 设水银密度为 ρ , 玻璃管横截面积为 S , 重力加速度为 g , 右端液面上升高度为 L 0 A 气体初状态压强为 p A 0 =p 0 + ρ gh= 80 cmHg, 体积 V 10 =hS A 气体末状态压强为 p A =p 0 + 2 ρ gh= 84 cmHg, 体积为 V 1 =L A S B 气体初状态压强为 p B 0 =p A 0 - 2 ρ gh= 72 cmHg, 体积 V 20 =LS B 气体末状态压强为 p B =p A - 2 ρ gh- 2 ρ gL 0 = (76 - 2 L 0 ) cmHg; 体积为 V 2 = ( L-L 0 ) S 根据玻意耳定律 , 有 p B 0 LS=p B ( L-L 0 ) S , p A 0 hS=p A L A S 联立可得 : L 0 = 0 . 5 cm 　 L A ≈3 . 8 cm 答案 : 0 . 5 cm 　 3 . 8 cm 考点 1 考点 2 考点 3 “ 汽缸活塞类 ” 模型 例 2 (2019 广东二模 ) 如图所示 , 甲、乙两个竖直放置的相同汽缸中装有体积均为 V 0 、热力学温度均为 T 0 的理想气体 , 两汽缸用细管 ( 容积不计 ) 连接 , 细管中有一绝热轻小活塞 ; 汽缸乙上方有一横截面积为 S 、质量不计的大活塞。现将汽缸甲中的气体缓慢升温到 T 0 , 同时在大活塞上增加砝码 , 稳定后细管中的小活塞仍停在原位置 , 外界大气压强为 p 0 , 乙汽缸中气体温度保持不变 , 两汽缸内气体的质量及一切摩擦均不计 , 重力加速度大小为 g 。求 (1) 大活塞上增加的砝码的质量 m ; (2) 大活塞下移的距离 L 。 解题思路 (1) 对甲中气体 , 体积不变 , 根据查理定律求解加热后压强 ; 然后对大活塞受力分析 , 根据受力平衡列式求解 ; (2) 对乙气体 , 温度不变 , 根据玻意耳定律列式求解。 考点 1 考点 2 考点 3 考点 1 考点 2 考点 3 方法归纳 汽缸活塞类问题的解决思路及常见类型 汽缸活塞类问题是热学部分典型的物理综合题 , 它需要考虑气体、汽缸或活塞等多个研究对象 , 涉及热学、力学等物理知识 , 需要灵活、综合地应用相关知识来解决问题。 1 . 一般思路 (1) 研究对象分两类 : 一类是热学研究对象 ( 一定质量的理想气体 ); 另一类是力学研究对象 ( 汽缸、活塞或某系统 ) 。 (2) 分析物理过程 , 对热学研究对象分析清楚初、末状态及状态变化过程 , 依据气体实验定律列出方程 ; 对力学研究对象要正确地进行受力分析 , 依据力学规律列出方程。 (3) 挖掘题目的隐含条件 , 如几何关系等 , 列出辅助方程。 (4) 多个方程联立求解。对求解的结果注意检验它们的合理性。 考点 1 考点 2 考点 3 2 . 常见类型 (1) 气体系统处于平衡状态 , 需综合应用气体实验定律和物体的平衡条件解题。 (2) 气体系统处于力学非平衡状态 , 需要综合应用气体实验定律和牛顿运动定律解题。 (3) 两个或多个汽缸封闭着几部分气体 , 并且汽缸之间相互关联的问题 , 解答时应分别研究各部分气体 , 找出它们各自遵循的规律 , 并写出相应的方程 , 还要写出各部分气体之间压强或体积的关系式 , 最后联立求解。 说明 当选择力学研究对象进行分析时 , 研究对象的选取并不唯一 , 可以灵活地选整体或部分为研究对象进行受力分析 , 列出平衡方程或动力学方程。 考点 1 考点 2 考点 3 对应训练 3 . (2019 云南二模 ) 如图所示 , 导热汽缸由半径不同的两个圆柱形容器组成 , 汽缸上部横截面积为 1 . 5 S , 深度为 0 . 5 L , 下部横截面积为 S , 深度为 L , 侧面有阀门 C , C 处于打开状态。活塞上表面通过滑轮与一水桶相连。关闭阀门后向水桶中缓慢加水 , 使活塞上升到距汽缸上口 0 . 3 L 处停下。已知 : 大气压强为 p 0 , 室温为 T 0 , 重力加速度为 g , 不计一切摩擦 , 忽略水桶质量、活塞厚度及活塞质量。求 : (1) 加入水桶中水的质量 ; (2) 将水桶中的水取走一半 , 并对缸中气体缓慢加热 , 当活塞再次停于离汽缸上口 0 . 3 L 处时 , 气体的温度。 考点 1 考点 2 考点 3 考点 1 考点 2 考点 3 4 . (2019 安徽二模 ) 如图所示 , 两端开口的汽缸在水平方向上固定 , A 、 B 是两个厚度不计的活塞 , 可在汽缸内无摩擦地滑动 , 其面积分别为 S 1 = 20 cm 2 、 S 2 = 10 cm 2 , 它们之间用一根细杆连接 , B 通过水平方向上的轻细绳绕过定滑轮与重物 C 连接 , 静止时汽缸中气体的温度 T= 600 K, 压强 p 1 = 1 . 2 × 10 5 Pa, 汽缸两部分的气柱长均为 L 。已知大气压强 p 0 = 1 × 10 5 Pa, g 取 10 m/s 2 , 缸内气体可看作理想气体。求 : (1) 重物 C 的质量 ; (2) 若要保持汽缸内的压强不变 , 汽缸内温度的变化范围是多少 ? 考点 1 考点 2 考点 3 解析 : (1) 活塞整体受力平衡 , 由平衡条件得 : p 1 S 1 +p 0 S 2 =p 0 S 1 +p 1 S 2 +Mg , 代入数据解得 : M= 2 kg; (2) 若要保持汽缸内的压强不变 , 温度升高时向左运动 , 最多移动 L , 解得 : T 1 = 800 K; 若要保持汽缸内的压强不变 , 温度降低时向右运动 , 最多移动 L , 解得 : T 2 = 400 K; 所以 400 K≤ T ≤800 K 。 答案 : (1)2 kg 　 (2)400 K≤ T ≤800 K 考点 1 考点 2 考点 3 “ 变质量气体 ” 模型 例 3 (2019 四川成都二模 ) 如图所示为一个带有阀门 K 、容积为 2 dm 3 的容器 ( 容积不可改变 ) 。先打开阀门让其与大气连通 , 再用打气筒向里面打气 , 打气筒活塞每次可以打进 1 × 10 5 Pa 、 200 cm 3 的空气 , 忽略打气和用气时气体的温度变化 ( 设外界大气的压强 p 0 = 1 × 10 5 Pa) (1) 若要使气体压强增大到 5 . 0 × 10 5 Pa, 应打多少次气 ? (2) 若上述容器中装的是 5 . 0 × 10 5 Pa 的氧气 , 现用它给容积为 0 . 7 dm 3 的真空瓶充气 , 使瓶中的气压最终达到符合标准的 2 . 0 × 10 5 Pa, 则可充多少瓶 ? 考点 1 考点 2 考点 3 审题 考点 1 考点 2 考点 3 解析 : (1) 设需要打气 n 次 , 因每次打入的气体相同 , 故可视 n 次打入的气体一次性打入 , 则气体的初状态 : p 1 = 1 . 0 × 10 5 Pa, V 1 =V 0 +n Δ V 末状态 : p 2 = 5 . 0 × 10 5 Pa, V 2 =V 0 其中 : V 0 = 2 dm 3 ,Δ V= 0 . 2 dm 3 由玻意耳定律得 : p 1 V 1 =p 2 V 2 代入数据解得 : n= 40( 次 ); (2) 设气压为 2 . 0 × 10 5 Pa 时气体的体积为 V 3 , 则 p 3 = 2 . 0 × 10 5 Pa 由玻意耳定律有 : p 2 V 2 =p 3 V 3 代入数据解得 : V 2 = 2 dm 3 真空瓶的容积为 V 瓶 = 0 . 7 dm 3 答案 : (1)40 次 　 (2)4 瓶 考点 1 考点 2 考点 3 方法归纳 变质量气体问题分类及处理方法 分析变质量气体问题时 , 要通过巧妙地选择研究对象 , 使变质量气体问题转化为定质量气体问题 , 用气体实验定律求解。 (1) 打气问题 : 选择原有气体和即将充入的气体作为研究对象 , 就可把充气过程中气体质量变化问题转化为定质量气体的状态变化问题。 (2) 抽气问题 : 将每次抽气过程中抽出的气体和剩余气体作为研究对象 , 质量不变 , 故抽气过程可以看成是等温膨胀过程。 (3) 灌气问题 : 把大容器中的剩余气体和多个小容器中的气体整体作为研究对象 , 可将变质量问题转化为定质量问题。 (4) 漏气问题 : 选容器内剩余气体和漏出气体整体作为研究对象 , 便可使问题变成一定质量气体的状态变化 , 可用理想气体的状态方程求解。 考点 1 考点 2 考点 3 对应训练 5 . (2019 河北衡水模拟 ) 如图所示 , 喷雾器内有 13 L 药液 , 上部封闭有 1 atm 的空气 2 L, 关闭喷雾阀门 , 用打气筒活塞每次可以打进 1 atm 、 160 cm 3 的空气 , 设外界环境温度一定 , 忽略打气和喷药过程气体温度的变化 , 空气可看作理想气体 , 求 : (1) 要使喷雾器内气体压强增大到 3 atm, 打气筒应打气的次数 n ; (2) 若压强达到 3 atm 时停止打气 , 并开始向外喷药 , 那么当喷雾器不能再向外喷药时 , 桶内剩下的药液的体积 ; (3) 打开喷雾阀门 , 喷雾过程中封闭气体可以看成等温膨胀 , 此过程气体是吸热还是放热 ? 简要说明理由。 考点 1 考点 2 考点 3 解析 : (1) 设应打气 n 次 , 则有 p 1 = 1 atm, V 1 = 0 . 16 n L + 2 L p 2 = 3 atm, V 2 = 2 L 根据玻意耳定律得 p 1 V 1 =p 2 V 2 , 解得 : n= 25( 次 ) (2) 由题意可知 V 1 '= 2 L, p 1 '= 3 atm, p 2 '= 1 atm, 根据玻意耳定律得 : p 1 'V 1 '=p 2 'V 2 ' 解得 V 2 '= 6 L 剩下的药液 V= 15 L - 6 L = 9 L (3) 气体对外做功而内能不变 , 根据热力学第一定律可得气体吸热。 答案 : (1)25 　 (2)9 L 　 (3) 吸热 考点 1 考点 2 考点 3 6 . (2019 甘肃兰州模拟 ) 容器内装有 1 kg 的氧气 , 开始时 , 氧气压强为 1 . 0 × 10 6 Pa, 温度为 57 ℃ , 因为漏气 , 经过一段时间后 , 容器内氧气压强变为原来的 , 温度降为 27 ℃ , 求漏掉多少千克氧气 ? 考点 1 考点 2 考点 3 答案 : 0 . 34 kg