江苏省赣榆高级中学2019年高考高三物理实验、计算试题每日一练（23） 5页

分 数 江苏省赣榆高级中学2019年高考高三物理实验、计算试题每日一练（23）‎ 完成时间： 月 日 点 分---- 点 分， ‎ ‎1. 碰撞的恢复系数的定义为，其中v10和v20分别是碰撞前两物体的速度，v1和v2分别是碰撞后物体的速度。弹性碰撞的恢复系数e=1，非弹性碰撞的e<1。某同学借用验证动力守恒定律的实验装置（如图所示）验证弹性碰撞的恢复系数是否为1，实验中使用半径相等的钢质小球1和2（它们之间的碰撞可近似视为弹性碰撞），且小球1的质量大于小球2的质量。‎ 实验步骤如下：‎ 安装好实验装置，做好测量前的准备，并记下重锤线所指的位置O。‎ 第一步，不放小球2，让小球1从斜槽上A点由静止滚下，并落在地面上。重复多次，用尽可能小的圆把小球的所落点圈在里面，其圆心就是小球落点的平均位置。‎ 第二步，把小球2 放在斜槽前端边缘处C点，让小球1从A点由静止滚下，使它们碰撞。重复多次，并使用与第一步同样的方法分别标出碰撞后小球落点的平均位置。‎ 第三步，用刻度尺分别测量三个落地点的平均位置离O点的距离，即线段OM、OP、ON的长度。‎ 上述实验中，‎ ‎①P点是 平均位置，‎ M点是 平均位置，‎ N点是 平均位置。‎ ‎②请写出本实验的原理 ，写出用测量量表示的恢复系数的表达式 。‎ ‎③三个落地点距O点的距离OM、OP、ON与实验所用的小球质量是否有关系？‎ ‎ 。‎ ‎2. 测量一只量程已知的电压表内阻，器材如下：‎ V A. 待测电压表 （量程3V，内阻约3KΩ)‎ A B．电流表 （量程0.6A，内阻0.01Ω）‎ C. 定值电阻 R （阻值2KΩ，额定电流0.5A）‎ D．电源E（电动势约3V，内阻不计）‎ E．开关两只，S1、S2，导线若干 ‎（1）某同学设计了如图(甲)所示的测量电路，在实验操作时，发现不可行。你认为主要 是 。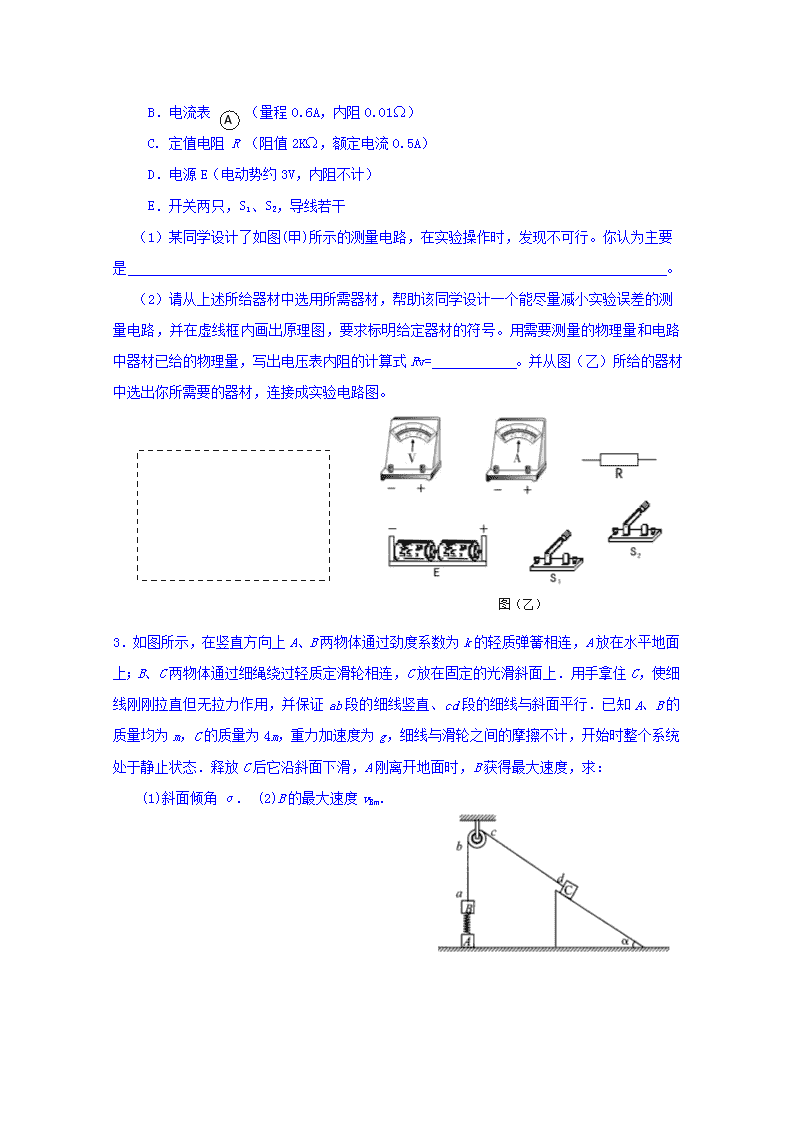‎ ‎（2）请从上述所给器材中选用所需器材，帮助该同学设计一个能尽量减小实验误差的测 量电路，并在虚线框内画出原理图，要求标明给定器材的符号。用需要测量的物理量和电路中器材已给的物理量，写出电压表内阻的计算式Rv= 。并从图（乙）所给的器材中选出你所需要的器材，连接成实验电路图。‎ 图（乙）‎ ‎3．如图所示，在竖直方向上A、B两物体通过劲度系数为k的轻质弹簧相连，A放在水平地面上；B、C两物体通过细绳绕过轻质定滑轮相连，C放在固定的光滑斜面上．用手拿住C，使细线刚刚拉直但无拉力作用，并保证ab段的细线竖直、cd段的细线与斜面平行．已知A、B的质量均为m，C的质量为4m，重力加速度为g，细线与滑轮之间的摩擦不计，开始时整个系统处于静止状态．释放C后它沿斜面下滑，A刚离开地面时，B获得最大速度，求： ‎ ‎(1)斜面倾角α． (2)B的最大速度vBm．‎ 参 考 答 案 ‎1. （Ⅰ）① 1.88m (1分) , 1.96m (1分) , 该实验小组做实验时先释放了纸带，然后再 合上打点计时器的电键 或者 释放纸带时手抖动了(1分) (其他答案只要合理均给满分)‎ ‎② D (2分), 重力加速度g (1分) ‎ ‎（Ⅱ）①P点是在实验的第一步中小球1落点的平均位置； M点是小球1与小球2碰后小球1落点的平均位置； N点是小球2落点的平均位置 (3分)‎ ‎②小球从槽口C飞出后作平抛运动的时间相同，假设为 t,则有 ‎ (3分)‎ 小球2碰撞前静止，即 ‎ (2分)‎ ‎③OP与小球的质量无关，OM和ON与小的质量有关 (2分)‎ ‎2. （1）不可行理由：电流表量程太大，而电路中电流太小，电流表没有明显读数。（3分）‎ ‎（2） 电路图（2分） 连线（2分）‎ ‎（乙）‎ ‎ （2分） ‎ ‎3. 解：（1）设当物体A刚刚离开地面时，弹簧的伸长量为为xA，由： ‎ kxA=mg （1分）‎ 此时以B为研究对象，物体B受到重力mg、弹簧的弹力kxA、细线的拉力T三个力的作用．设物体B的加速度为a，根据牛顿第二定律，‎ 对B有： T—mg—kxA=ma （1分）‎ 对C有： 4mgsinα—T=4ma （1分）‎ 由以上两式得：4mgsinα—mg—kxA =5ma （1分）‎ 当B获得最大速度时，有： a = 0 （1分）‎ ‎ 解得：sinα=1/2 （1分）‎ 所以：α=300 （1分）‎ ‎（2）开始时弹簧压缩的长度为：xB=mg/k （2分）‎ 当物体A刚离开地面时，物体B上升的距离以及物体C沿斜面下滑的距离为：‎ ‎ h=xA+ xB （2分）‎ 由于xA＝xB，弹簧处于压缩状态和伸长状态时的弹性势能相等，弹簧弹力做功为零。且物体A刚刚离开地面时，B、C两物体的速度相等，设为vBm，由动能定理：‎ ‎ （2分）‎ 解得： （2分）‎