2018-2019学年广东省梅州市高一下学期期末考试物理试题（word版） 10页

‎2018-2019学年广东省梅州市高一下学期期末考试 高一物理 一、单项选择题（本大题共8小题，每小题，共24分。每小题给出的四个选项中，只有一个选项符合题目要求，选对的得，选错或不答的得0分。）‎ ‎1.下列关于物理学史的说法正确的是（ ）‎ A. 伽利略最早提出了“日心说”‎ B. 卡文迪许第一次测出了引力常量 C. 开普勒发现了万有引力定律 D. 第谷发现行星的运行轨道是椭圆 ‎【答案】B ‎2.在越野赛车时，一辆赛车在水平公路上减速转弯，从俯视图中可以看到赛车沿曲线由M向N行驶。下图中分别画出了汽车转弯时所受合力F的四种方向，你认为正确的是（）‎ A. B. ‎ C. D. ‎ ‎【答案】C ‎3.一个人站在阳台上，在同一位置以相同的速率分别把相同质量的三个球竖直向上、竖直向下和水平抛出．若小球所受空气阻力均可忽略不计，则三个球落地时重力的功率大小比较是（　　）‎ A. 平抛球最小 B. 下抛球最小 C. 上抛球最小 D. 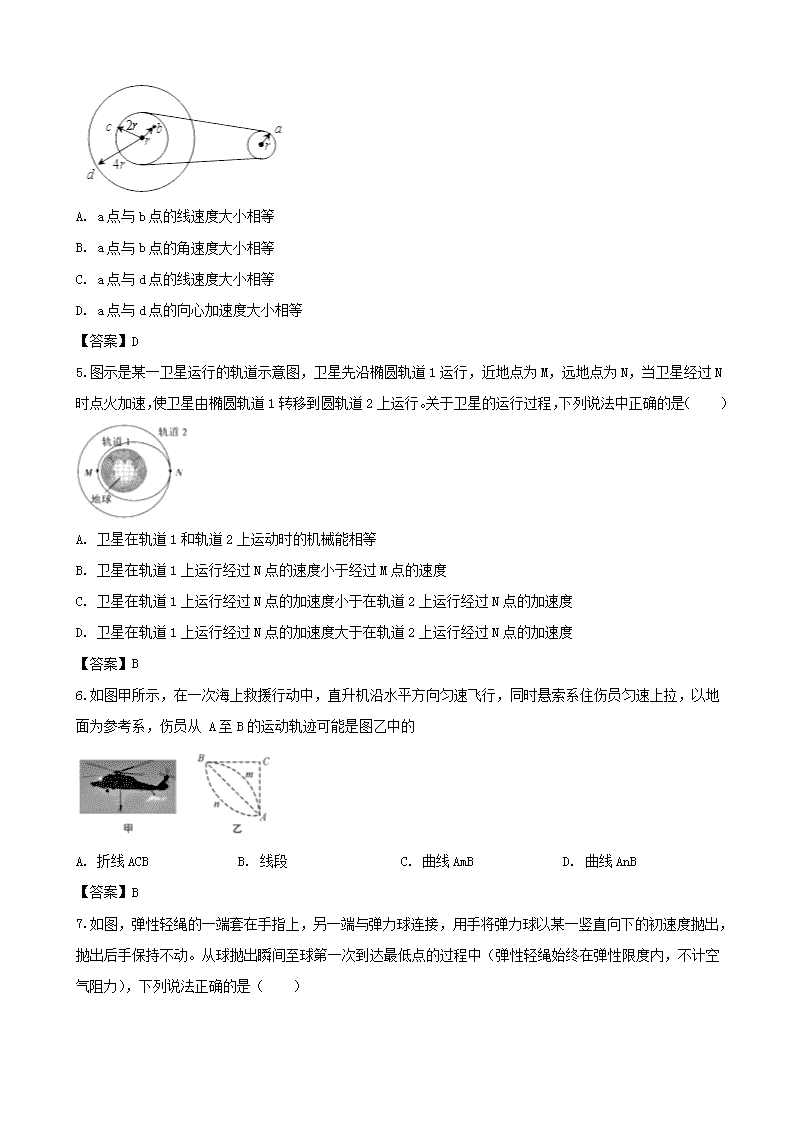三球一样大 ‎【答案】A ‎4.如图所示为一皮带传动装置，右轮的半径为r，a是它边缘上的一点，左侧是一轮轴，大轮的半径是4r，小轮的半径为2r，b点在小轮上，到小轮中心的距离为r，c点和d点分别位于小轮和大轮的边缘上，若在传动过程中，皮带不打滑，则（　　）‎ A. a点与b点的线速度大小相等 B. a点与b点的角速度大小相等 C. a点与d点的线速度大小相等 D. a点与d点的向心加速度大小相等 ‎【答案】D ‎5.图示是某一卫星运行的轨道示意图，卫星先沿椭圆轨道1运行，近地点为M，远地点为N，当卫星经过N时点火加速，使卫星由椭圆轨道1转移到圆轨道2上运行。关于卫星的运行过程，下列说法中正确的是（　　）‎ A. 卫星在轨道1和轨道2上运动时的机械能相等 B. 卫星在轨道1上运行经过N点的速度小于经过M点的速度 C. 卫星在轨道1上运行经过N点的加速度小于在轨道2上运行经过N点的加速度 D. 卫星在轨道1上运行经过N点的加速度大于在轨道2上运行经过N点的加速度 ‎【答案】B ‎6.如图甲所示，在一次海上救援行动中，直升机沿水平方向匀速飞行，同时悬索系住伤员匀速上拉，以地面为参考系，伤员从 A至B的运动轨迹可能是图乙中的 A. 折线ACB B. 线段 C. 曲线AmB D. 曲线AnB ‎【答案】B ‎7.如图，弹性轻绳的一端套在手指上，另一端与弹力球连接，用手将弹力球以某一竖直向下的初速度抛出，抛出后手保持不动。从球抛出瞬间至球第一次到达最低点的过程中（弹性轻绳始终在弹性限度内，不计空气阻力），下列说法正确的是（　　）‎ A. 绳刚伸直时，球的动能最大 B. 该过程中，球的机械能守恒 C. 该过程中，重力对球做的功等于球克服绳的拉力做的功 D. 该过程中，轻绳的弹性势能和小球的动能之和一直增大 ‎【答案】D ‎8.引体向上是中学生体育测试的项目之一，引体向上运动的吉尼斯世界纪录是53次/分钟。若一个普通中学生在30秒内完成12次引体向上，该学生此过程中克服重力做功的平均功率最接近于（　　）‎ A. 5W B. 20W C. 100W D. 400W ‎【答案】C 二、多项选择题（本大题共4小题，每小题4分，共16分。每小题给出的四个选项中，有两个选项符合题目要求，全部选对的得4分，选对单不全的得，有选错或不答的得0分。）‎ ‎9.物体做匀速圆周运动时,下列物理量中变化的是（　　）‎ A. 线速度 B. 角速度 C. 向心加速度 D. 动能 ‎【答案】AC ‎10.正在水平匀速飞行的飞机，每隔1秒钟释放一个小球，先后共释放5个。不计阻力则（ ）‎ A. 这5个球在空中排成一条直线 B. 这5个球在空中处在同一抛物线上 C. 在空中，第1、2两球间的距离保持不变 D. 相邻两球的落地点间距离相等 ‎【答案】AD ‎11.如图所示，下列关于地球人造卫星轨道的说法，正确的是 （ ）‎ A. 卫星轨道a、b、c都是可能的 B. 卫星轨道只可能是b、c C. 同步卫星轨道可能是b D. a、b均可能是同步卫星轨道 ‎【答案】BC ‎12.2022年第24届冬季奥林匹克运动会将在中国举行，跳台滑雪是其中最具观赏性的项目之一。跳台滑雪赛道可简化为助滑道、着陆坡、停止区三部分，如图所示。一次比赛中，质量m的运动员从A处由静止下滑，运动到B处后水平飞出，落在了着陆坡末端的C点，滑入停止区后，在与C等高的D处速度减为零。已知B、C之间的高度差为h，着陆坡的倾角为θ，重力加速度为g。只考虑运动员在停止区受到的阻力，不计其他能量损失。由以上信息可以求出（　　）‎ A. 运动员在空中飞行的时间 B. A、B之间高度差 C. 运动员在停止区运动过程中阻力的大小 D. C、D两点之间的水平距离 ‎【答案】AB 三、实验题（第14题（1）问，其他每空，共20分）‎ ‎13.在利用重锤下落验证机械能守恒定律的实验中：‎ ‎（1）实验中动能的增加量略小于重力势能的减少量，其主要原因是_____‎ A、重物下落的实际距离大于测量值 B、重物下落的实际距离小于测量值 C、重物下落受到阻力 D、重物的实际末速度大于计算值 ‎（2）如图所示，有一条纸带，各点距A点的距离分别为d1，d2，d3‎ ‎，，各相邻点间的时间间隔为T，当地重力加速度为g，要用它来验证物体从B到G处的机械能是否守恒，则B点的速度表达式为vB＝_____，G点的速度表达式为vG＝_____，‎ ‎（3）若B点和G点的速度vB、vG以及BG间的距离h均为已知量，则当满足_____时，物体的机械能守恒．‎ ‎【答案】 (1). C (2). (3). (4). VG2−VB2＝2gh ‎14.在“探究功与速度变化的关系”实验中，某同学设计了如图甲所示的实验方案：使小物块在橡皮筋的作用下沿水平桌面被弹出，第二次、第三次操作时分别改用2根、3根、同样的橡皮筋将小物块弹出，测出小物块被弹出时速度，然后找到牵引力对小物块做的功与小物块速度的关系。‎ ‎（1）要测得小物块被弹出后的水平速度，需要测量哪些物理量（填正确答案标号，g已知）_____‎ A．小物块的质量m B．橡皮筋的原长x C．橡皮筋的伸长量 D．桌面到地面的高度h E．小物块抛出点到落地点的水平距离L ‎（2）实验时，若把橡皮筋两端固定，使橡皮筋的伸长量依次加倍来实现橡皮筋对小物块做功成整数倍变化，这样做有什么不好？答：_____________________________‎ ‎（3）根据实验数据做出的图象如图乙所示，图线不通过原点的原因是__________________‎ ‎【答案】 (1). DE (2). 橡皮筋的伸长量不同，会造成每一次小物体克服摩擦力做的功不同，不利于比较它们的关系 (3). 物体在桌面上运动时需要克服摩擦力做功 四、计算题（本题共4小题，共40分。解答时应写出必要的文字说明、方程式和重要演算步骤。只写出最后答案的不能得分，答案中必须写出数值和单位）‎ ‎15.已知小船在静水中的速度为5m/s，水流速度为3m/s，河宽度为600m，求：‎ ‎（1）若要使小船最短时间过河，最短时间为多少？‎ ‎（2）若要小船到最短位移过河，过河时间为多少？‎ ‎【答案】（1）（2）150s ‎（1）船头垂直于岸渡河时间最短 最短时间：‎ 解得： ‎ ‎（2）当合速度与河岸方向垂直时，渡河航程最短 依题意有：合速度的大小为： ‎ 则渡河的时间为： ‎ 联立以上两式，解得：t=150s ‎16.已知“天宫一号”在地球上空的圆轨道上运行时离地面的高度为h。地球半径为R，地球表面的重力加速度为g，万有引力常量为G．求：‎ ‎（1）“天宫一号”在该圆轨道上运行时速度v的大小；‎ ‎（2）“天宫一号”在该圆轨道上运行时重力加速度g’的大小；‎ ‎【答案】（1）（2）‎ ‎（1）地球表面质量为m0的物体，有：① ‎ ‎“天宫一号”在该圆轨道上运行时万有引力提供向心力：‎ ‎② ‎ 联立①②两式得：飞船在圆轨道上运行时速度：‎ ‎（2）根据 ③‎ 联立①③解得：‎ ‎17.质量的行李箱放在水平地面上，行李箱与地面的动摩擦因数为，用与水平成、斜向上的大小为的拉力拉动行李箱，使行李箱由静止开始沿水平地面运动，5s后撤去拉力。求：‎ 撤去拉力瞬间行李箱的速度v 拉力做的功 全程摩擦力对行李箱所做的功。‎ ‎【答案】，（3）-600J 对行李箱受力分析如图所示 设物体受摩擦力为f，支持力为N，则 根据牛顿第二定律有：‎ 水平方向有 竖直方向有 解得：‎ 撤去拉力瞬间行李箱的速度 内行李箱的位移 拉力做的功 设全程摩擦力对行李箱所做功为。‎ 根据动能定理得 解得 ‎18.如图所示，在水平轨道右侧固定半径为R的竖直圆槽形光滑轨道，水平轨道的PQ段长度为，上面铺设特殊材料，小物块与其动摩擦因数为，轨道其它部分摩擦不计。水平轨道左侧有一轻质弹簧左端固定，弹簧处于原长状态。可视为质点的质量的小物块从轨道右侧A点以初速度冲上轨道，通过圆形轨道，水平轨道后压缩弹簧，并被弹簧以原速率弹回，取，求：‎ ‎（1）弹簧获得的最大弹性势能；‎ ‎（2）小物块被弹簧第一次弹回经过圆轨道最低点时的动能；‎ ‎（3）当R满足什么条件时，小物块被弹簧第一次弹回圆轨道时能沿轨道运动而不会脱离轨道。‎ ‎【答案】（1）10.5J（2）3J（3）0.3m≤R≤0.42m或0≤R≤0.12m ‎1）当弹簧被压缩到最短时，其弹性势能最大。从A到压缩弹簧至最短过程中，由动能定理得：  −μmgl+W弹＝0−mv02 由功能关系：W弹=-△Ep=-Ep 解得 Ep=10.5J； （2）小物块从开始运动到第一次被弹回圆形轨道最低点的过程中，由动能定理得   −2μmgl＝Ek−mv02 解得 Ek=3J； （3）小物块第一次返回后进入圆形轨道的运动，有以下两种情况： ①小球能够绕圆轨道做完整的圆周运动，此时设小球最高点速度为v2，由动能定理得   −2mgR＝mv22−Ek 小物块能够经过最高点的条件m≥mg，解得 R≤0.12m ②小物块不能够绕圆轨道做圆周运动，为了不让其脱离轨道，小物块至多只能到达与圆心等高的位置，即 mv12≤mgR，解得R≥0.3m； 设第一次自A点经过圆形轨道最高点时，速度为v1，由动能定理得：‎ ‎−2mgR＝mv12-mv02‎ 且需要满足 m≥mg，解得R≤0.72m， 综合以上考虑，R需要满足的条件为：0.3m≤R≤0.42m或0≤R≤0.12m。‎ ‎ ‎