新课标2020高考物理二轮复习专题强化训练2力和直线运动含解析 11页

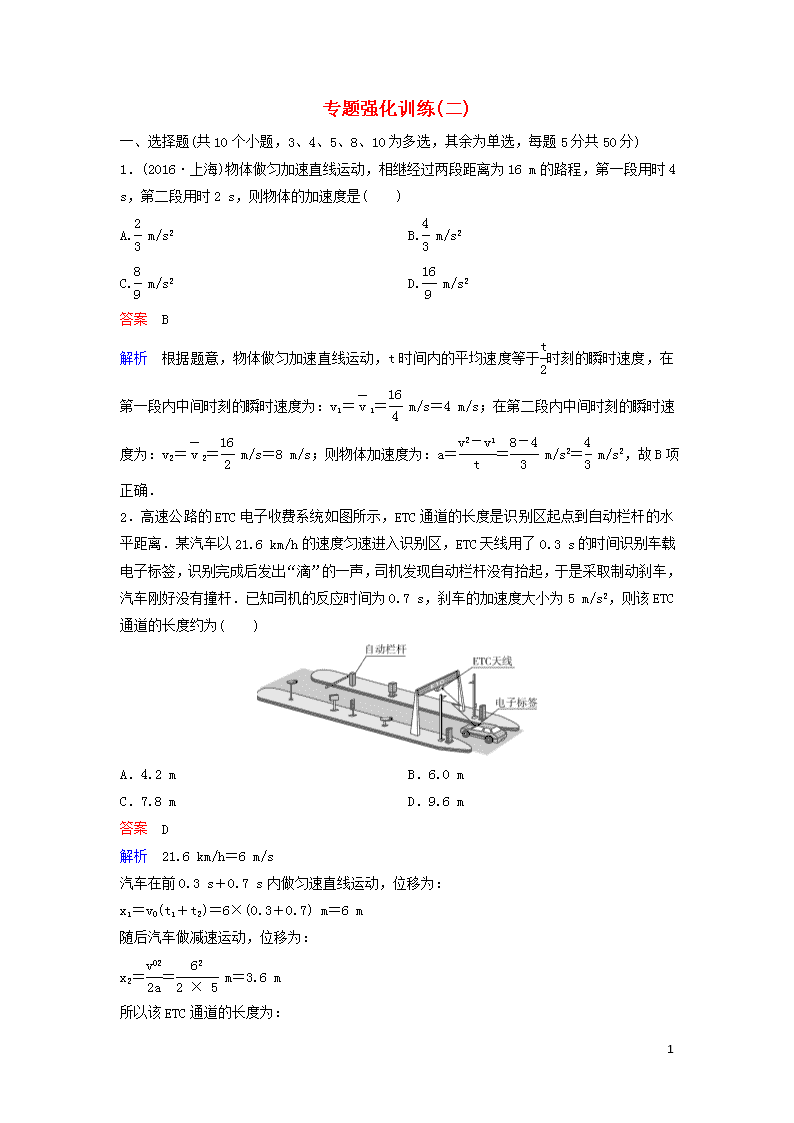
专题强化训练(二)‎ 一、选择题(共10个小题，3、4、5、8、10为多选，其余为单选，每题5分共50分)‎ ‎1．(2016·上海)物体做匀加速直线运动，相继经过两段距离为16 m的路程，第一段用时4 s，第二段用时2 s，则物体的加速度是(　　)‎ A. m/s2　　　　　　　　 B. m/s2‎ C. m/s2 D. m/s2‎ 答案　B 解析　根据题意，物体做匀加速直线运动，t时间内的平均速度等于时刻的瞬时速度，在第一段内中间时刻的瞬时速度为：v1＝1＝ m/s＝4 m/s；在第二段内中间时刻的瞬时速度为：v2＝2＝ m/s＝8 m/s；则物体加速度为：a＝＝ m/s2＝ m/s2，故B项正确．‎ ‎2．高速公路的ETC电子收费系统如图所示，ETC通道的长度是识别区起点到自动栏杆的水平距离．某汽车以21.6 km/h的速度匀速进入识别区，ETC天线用了0.3 s的时间识别车载电子标签，识别完成后发出“滴”的一声，司机发现自动栏杆没有抬起，于是采取制动刹车，汽车刚好没有撞杆．已知司机的反应时间为0.7 s，刹车的加速度大小为5 m/s2，则该ETC通道的长度约为(　　)‎ A．4.2 m B．6.0 m C．7.8 m D．9.6 m 答案　D 解析　21.6 km/h＝6 m/s 汽车在前0.3 s＋0.7 s内做匀速直线运动，位移为：‎ x1＝v0(t1＋t2)＝6×(0.3＋0.7) m＝6 m 随后汽车做减速运动，位移为：‎ x2＝＝ m＝3.6 m 所以该ETC通道的长度为：‎ L＝x1＋x2＝(6＋3.6) m＝9.6 m 11‎ 故A、B、C三项错误，D项正确．‎ ‎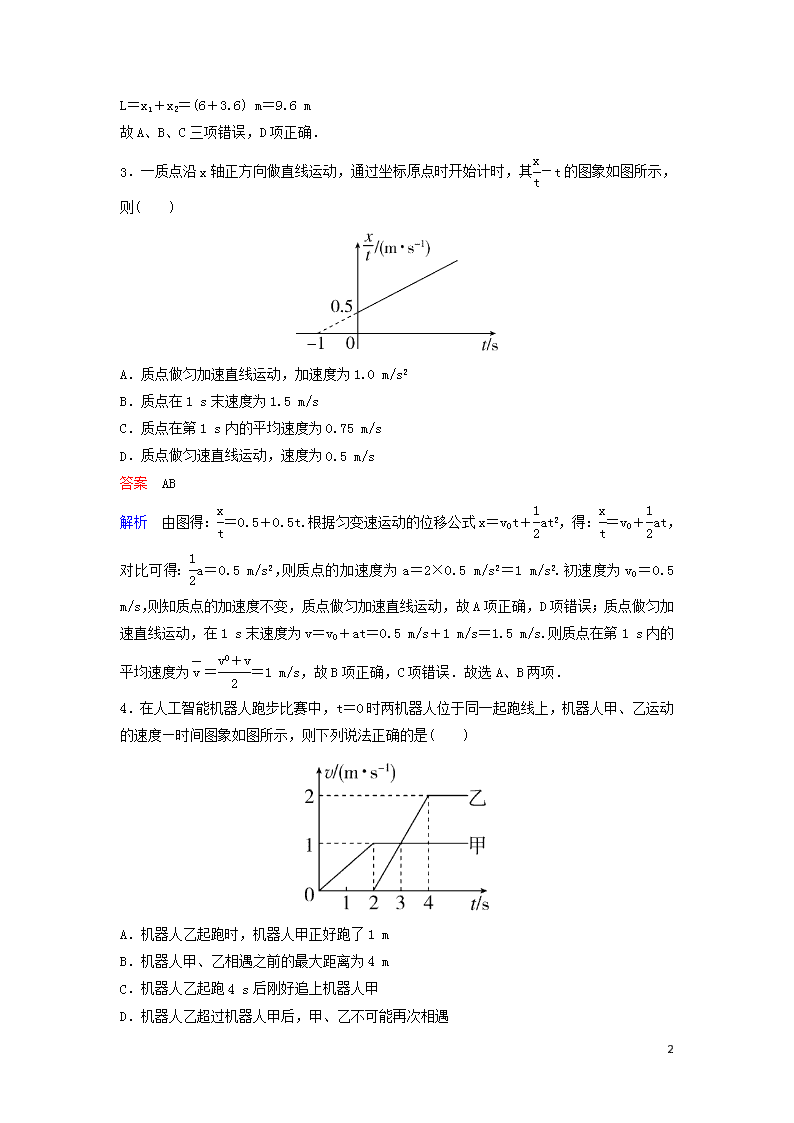3．一质点沿x轴正方向做直线运动，通过坐标原点时开始计时，其－t的图象如图所示，则(　　)‎ A．质点做匀加速直线运动，加速度为1.0 m/s2‎ B．质点在1 s末速度为1.5 m/s C．质点在第1 s内的平均速度为0.75 m/s D．质点做匀速直线运动，速度为0.5 m/s 答案　AB 解析　由图得：＝0.5＋0.5t.根据匀变速运动的位移公式x＝v0t＋at2，得：＝v0＋at，对比可得：a＝0.5 m/s2，则质点的加速度为a＝2×0.5 m/s2＝1 m/s2.初速度为v0＝0.5 m/s，则知质点的加速度不变，质点做匀加速直线运动，故A项正确，D项错误；质点做匀加速直线运动，在1 s末速度为v＝v0＋at＝0.5 m/s＋1 m/s＝1.5 m/s.则质点在第1 s内的平均速度为＝＝1 m/s，故B项正确，C项错误．故选A、B两项．‎ ‎4．在人工智能机器人跑步比赛中，t＝0时两机器人位于同一起跑线上，机器人甲、乙运动的速度—时间图象如图所示，则下列说法正确的是(　　)‎ A．机器人乙起跑时，机器人甲正好跑了1 m B．机器人甲、乙相遇之前的最大距离为4 m C．机器人乙起跑4 s后刚好追上机器人甲 D．机器人乙超过机器人甲后，甲、乙不可能再次相遇 答案　AD 11‎ 解析　机器人乙在t＝2 s时起跑，此时机器人甲正好跑过的距离x＝ m＝1 m，故A项正确；当两机器人的速度相等时相距最远，两者间的最大距离等于0～3 s内位移之差，即xmax＝ m＋ m＝1.5 m，故B项错误；机器人乙起跑4 s后，甲通过的位移x甲＝×1 m＝5 m，乙通过的位移x乙＝×2 m＝6 m，知x乙>x甲，说明在机器人乙起跑4 s前乙追上甲，故C项错误；机器人乙超过机器人甲后，乙的速度总比甲的大，则甲、乙不可能再次相遇，故D项正确．故选A、D两项．‎ ‎5．如图甲所示，一质量为M的长木板静置于光滑水平面上，其上放置一质量为m的小滑块．木板受到随时间t变化的水平拉力F作用时，用传感器测出其加速度a，得到如图乙所示的a－F图．取g＝10 m/s2，则(　　)‎ A．滑块的质量m＝4 kg B．木板的质量M＝2 kg C．当F＝8 N时滑块加速度为2 m/s2‎ D．滑块与木板间的动摩擦因数为0.1‎ 答案　ABD 解析　当F等于6 N时，加速度为：a＝1 m/s2，对整体分析，由牛顿第二定律有：F＝(M＋m)a，代入数据解得：M＋m＝6 kg，当F大于6 N时，根据牛顿第二定律得：a＝＝F－，由图示图象可知，图线的斜率为：k＝＝＝＝，解得：M＝2 kg，滑块的质量为：m＝4 kg，故A、B两项正确；根据F大于6 N的图线知，F＝4时，a＝0，即：0＝×F－，代入数据解得：μ＝0.1，由图示图象可知，当F＝8 N时，滑块与木板相对滑动，滑块的加速度为：a＝μg＝1 m/s2，故C项错误，D项正确．‎ ‎6.如图所示，一固定杆与水平方向夹角为θ，将一质量为m1的滑块套在杆上，通过轻绳悬挂一个质量为m2的小球，杆与滑块之间的动摩擦因数为μ.若滑块与小球保持相对静止以相同的加速度a一起运动，此时绳子与竖直方向夹角为β，且θ<β，则滑块的运动情况是(　　)‎ 11‎ A．沿着杆加速下滑 B．沿着杆减速上滑 C．沿着杆减速下滑 D．沿着杆加速上滑 答案　B 解析　把滑块和球看作一个整体受力分析，沿斜面和垂直斜面建立直角坐标系，若速度方向向下，则沿斜面方向：(m1＋m2)gsinθ－f＝(m1＋m2)a，‎ 垂直斜面方向：‎ FN＝(m1＋m2)gcosθ 摩擦力：f＝μFN 联立可解得：a＝gsinθ－μgcosθ，‎ 对小球有：若θ＝β，a＝gsinβ 现有：θ<β，则有：a>gsinβ 所以gsinθ－μgcosθ>gsinβ，gsinθ－gsinβ>μgcosθ 因为θ<β，所以gsinθ－gsinβ<0，但μgcosθ>0，所以假设不成立，即速度的方向一定向上，由于加速度方向向下，所以物体沿着杆减速上滑，故B项正确．‎ ‎7．在两个足够长的固定的相同斜面体上(其斜面光滑)，分别有如图所示的两套装置，斜面体B的上表面水平且光滑，长方体D的上表面与斜面平行且光滑，p是固定在B、D上的小柱，完全相同的两只弹簧一端固定在p上，另一端分别连在A、C上，在A与B、C与D分别保持相对静止状态沿斜面自由下滑的过程中，下列说法正确的是(　　)‎ A．两弹簧都处于拉伸状态 B．两弹簧都处于压缩状态 C．弹簧L1处于压缩状态，弹簧L2处于原长 D．弹簧L1处于拉伸状态，弹簧L2处于压缩状态 答案　C 11‎ 解析　由于斜面光滑，它们整体沿斜面下滑的加速度相同，为gsinα.对于题图甲，以A为研究对象，重力与支持力的合力沿竖直方向，而A沿水平方向的加速度：ax＝acosα＝g·sinαcosα，该加速度由水平方向弹簧的弹力提供，所以弹簧L1处于压缩状态；对于题图乙，以C为研究对象，重力与斜面支持力的合力大小：F合＝mgsinα，即C不能受到弹簧的弹力，弹簧L2处于原长状态，故C项正确，A、B、D三项错误．‎ ‎8.如图所示，质量分别为3m和m的1、2两物块叠放在水平桌面上，物块2与桌面间的动摩擦因数为μ，物块1与物块2间的动摩擦因数为2μ.物块1和物块2的加速度大小分别用a1、a2表示，物块1与物块2间的摩擦力大小用f1表示，物块2与桌面间的摩擦力大小用f2表示，最大静摩擦力等于滑动摩擦力．当水平力F作用在物块1上，下列反映a和f变化的图线正确的是(　　)‎ 答案　AC 解析　物块1与2间的最大静摩擦力f12＝2μ·3mg＝6μmg，物块2与地面间的最大静摩擦力f2＝μ·4mg＝4μmg，当拉力F<4μmg时，1、2两物块静止不动，摩擦力随F的增大而增大，当物块1、2开始滑动而未发生相对滑动时，物块2与地面间的摩擦力为滑动摩擦力，故大小不变，对物块2分析可知，f1－4μmg＝ma，解得f1＝4μmg＋ma逐渐增大，当物块1与2刚好发生相对滑动时，物块2与地面间的摩擦力为滑动摩擦力，故大小不变，物体2产生的最大加速度a2＝＝2μg，对物块1，根据牛顿第二定律，此时的拉力为F，则F－f12＝3ma2，解得F＝12μmg，拉力继续增大，此后2做匀加速运动，1‎ 11‎ 做加速度增大的加速度运动，故A、C两项正确，B、D两项错误．‎ ‎9.如图所示，地面上某个空间区域存在这样的电场，水平虚线上方的场强为E1，方向竖直向下的匀强电场；虚线下方为场强E2，方向竖直向上的匀强电场．一个质量为m，带电量为＋q的小球从上方电场的A点由静止释放，结果刚好到达下方电场中与A关于虚线对称的B点，则下列结论正确的是(　　)‎ A．若A、B高度差为h，则UAB＝ B．带电小球在A、B两点电势能相等 C．在虚线上下方的电场中，带电小球运动的加速度相同 D．若E1＝，则两电场强度大小关系满足E2＝2E1‎ 答案　D 解析　对A到B的过程运用动能定理得：qUAB＋mgh＝0，解得：UAB＝，可知A、B的电势不相等，则带电小球在A、B两点电势能也不相等，故A、B两项错误；A到虚线速度由零加速至v，虚线到B速度由v减为零，位移相同，根据v2＝2ax，则加速度大小相等，方向相反，故C项错误；在上方电场，根据牛顿第二定律得：a1＝，在下方电场中，根据牛顿第二定律得，加速度大小为：a2＝，因为a1＝a2，解得：E2－E1＝，若E1＝，则有：E2＝2E1，故D项正确．故选D项．‎ ‎10.如图所示，水平传送带A、B两端相距x＝4 m，以v0＝4 m/s的速度(始终保持不变)顺时针运转，今将一小煤块(可视为质点)无初速度地轻放至A端，由于煤块与传送带之间有相对滑动，会在传送带上留下划痕．已知煤块与传送带间的动摩擦因数μ＝0.4，取重力加速度g＝10 m/s2，则下列说法正确的是(　　)‎ 11‎ A．煤块到A运动到B的时间是2.25 s B．煤块从A运动到B的时间是1.5 s C．划痕长度是2 m D．划痕长度是0.5 m 答案　BC 解析　煤块在传送带上匀加速运动时，根据牛顿第二定律有μmg＝ma，得a＝μg＝4 m/s2，当煤块速度和传送带速度相同时，位移为：x1＝＝2 m<4 m 因此煤块先加速后匀速，匀加速运动的时间为：‎ t1＝＝1 s 匀速运动的时间为：t2＝＝0.5 s 煤块从A运动到B的总时间为：t＝t1＋t2＝1.5 s，故A项错误，B项正确；在加速阶段产生相对位移即产生划痕，则划痕长度为：Δx＝v0t1－x1＝2 m，故C项正确，D项错误．故选B、C两项．‎ 二、计算题(共4个小题，11题11分，12题12分，13题12分，14题15分，共50分)‎ ‎11．元旦期间，小聪和家人出去游玩，在途中的十字路口，他们乘坐的小汽车正在等绿灯，绿灯亮后，小汽车以大小a＝0.8 m/s2的加速度启动，恰在此时，一辆匀速运动的大卡车以大小v＝7.2 m/s的速度从旁边超过．假设小汽车启动后一直以加速度a加速行驶，直路足够长，且前方没有其他车辆和行人．求：‎ ‎(1)从两车并行起到两车距离最大所经历的时间t1；‎ ‎(2)两车相遇之前的最大距离L；‎ ‎(3)从两车并行起到两车再次相遇所经历的时间t2.‎ 答案　(1)9 s　(2)32.4 m　(3)18 s 解析　(1)经分析可知，当两车的速度相等时，它们之间的距离最大，有：v＝at1‎ 解得：t1＝9 s.‎ ‎(2)两车速度相等时，小汽车和卡车行驶的距离分别为：x＝at12，x′＝vt1‎ 又：L＝x′－x 解得：L＝32.4 m.‎ 11‎ ‎(3)由运动学规律有：at22＝vt2‎ 解得：t2＝18 s.‎ ‎12.如图所示，质量M＝2.0 kg的木板静止在光滑水平桌面上，木板上放有一质量m＝1.0 kg的小铁块(可视为质点)，小铁块离木板左端的距离为L＝0.5 m，铁块与木板间的动摩擦因数为μ＝0.2.现用一水平向右的恒力F作用在木板上，使木板和铁块由静止开始运动，设铁块与木板间的最大静摩擦力等于滑动摩擦力，g取10 m/s2.则：‎ ‎(1)若要使铁块不从木板上滑出，求恒力的最大值F1；‎ ‎(2)若将木板从铁块下抽出历时1 s，求拉力F2的大小；‎ ‎(3)若地面粗糙，且与木板间的动摩擦因数为0.2.改用棒打击木板左侧，使木板瞬间获得向右的速度v0，求v0至少多大时才能使小铁块脱离木板．‎ 答案　(1)6 N　(2)8 N　(3) m/s 解析　(1)铁块受到的最大静摩擦力为：f1＝μmg 由牛顿第二定律得铁块的最大加速度为：a1＝ 对整体，由牛顿第二定律得：F1＝(M＋m)a1‎ 解得：F1＝6 N.‎ ‎(3)设木板抽出的加速度为a2，‎ 由题意得：a2t2－a1t2＝L 对木板，由牛顿第二定律得：F2－f1＝Ma2‎ 解得：F2＝8 N.‎ ‎(3)设经时间t′铁块滑到木板的最左端且二者速度相等，由牛顿第二定律得木板的加速度大小为：‎ a3＝＝4 m/s2‎ 由位移关系得：v0t′－a3t′2－a1t′2＝L a1t′＝v0－a3t′‎ 解得：v0＝ m/s.‎ ‎13.如图所示，一水平长为L＝2.25 m的传送带与平板紧靠在一起，且上表面在同一水平面，皮带以v0＝4 m/s匀速顺时针转动，现在传送带上左端静止放上一质量为m＝1 kg的煤块(视为质点)，煤块与传送带及煤块与平板上表面之间的动摩擦因数均为μ1‎ 11‎ ‎＝0.2.经过一段时间，煤块被传送到传送带的右端，此过程在传送带上留下了一段黑色痕迹，随后煤块在平稳滑上右端平板上的同时，在平板右侧施加一个水平向右恒力F＝17 N，F作用了t0＝1 s时煤块与平板速度恰好相等，此时刻撤去F.最终煤块没有从平板上滑下，已知平板质量M＝4 kg(重力加速度为g＝10 m/s2)，求：‎ ‎(1)传送带上黑色痕迹的长度；‎ ‎(2)平板与地面间的动摩擦因数μ2的大小；‎ ‎(3)平板上表面至少多长？(计算结果保留两位有效数字)‎ 答案　(1)3.75 m　(2)0.3　(3)1.6 m 解析　(1)对煤块由牛顿第二定律：μ1mg＝ma1‎ 得a1＝2 m/s2‎ 若煤块一直加速到右端，设到右端速度为v1得 v12＝2a1L 解得：v1＝3 m/s 因为v1μ1，共速后煤块将以a1匀减速到停止，而平板以a3匀减速到停止．‎ 对平板，由牛顿第二定律得：μ1mg－μ2(M＋m)g＝Ma3‎ 得a3＝－ m/s2‎ t2＝＝－ s＝ s 全过程平板位移为：s板＝(t0＋t2)‎ 11‎ 解得：s板＝ m 全过程煤块位移为：s煤＝＝ m 所以板长l＝s煤－s板≈1.6 m.‎ ‎14．一轻弹簧的一端固定在倾角为θ的固定光滑斜面的底部，另一端和质量为m的小物块a相连，如图所示．质量为m的小物块b紧靠a静止在斜面上，此时弹簧的压缩量为x0，从t＝0时开始，对b施加沿斜面向上的外力，使b始终做匀加速直线运动．经过一段时间后，物块a、b分离，再经过同样长的时间，b距其出发点的距离恰好也为x0.弹簧的形变始终在弹性限度内，重力加速度大小为g.求：‎ ‎(1)弹簧的劲度系数；‎ ‎(2)物块b加速度的大小；‎ ‎(3)在物块a、b分离前，外力大小随时间变化的关系式．‎ 答案　(1)　(2) ‎(3)F＝mgsinθ＋t2 解析　(1)对整体分析，根据平衡条件可知，沿斜面方向上重力的分力与弹簧弹力平衡，则有 kx0＝(m＋m)gsinθ 解得：k＝.①‎ ‎(2)由题意可知，b经两段相等的时间位移为x0.‎ 由匀变速直线运动相邻相等时间内位移关系的规律可知：＝②‎ 说明当形变量为x1＝x0－＝时二者分离；‎ 对m分析，因分离时a、b间没有弹力，则根据牛顿第二定律可知：‎ kx1－mgsinθ＝ma③‎ 联立①②③式，解得：a＝.‎ 11‎ ‎(3)设时间为t，则经时间t时，ab前进的位移为 x＝at2＝ 则形变量变为：Δx＝x0－x 对整体分析可知，由牛顿第二定律，有 F＋kΔx－gsinθ＝a 解得：F＝mgsinθ＋t2‎ 因分离时位移x＝ 由x＝＝at2，解得：t＝ 故应保证t< ，F表达式才能成立．‎ 11‎