人教版必修一3.2《弹力》WORD教案9 4页

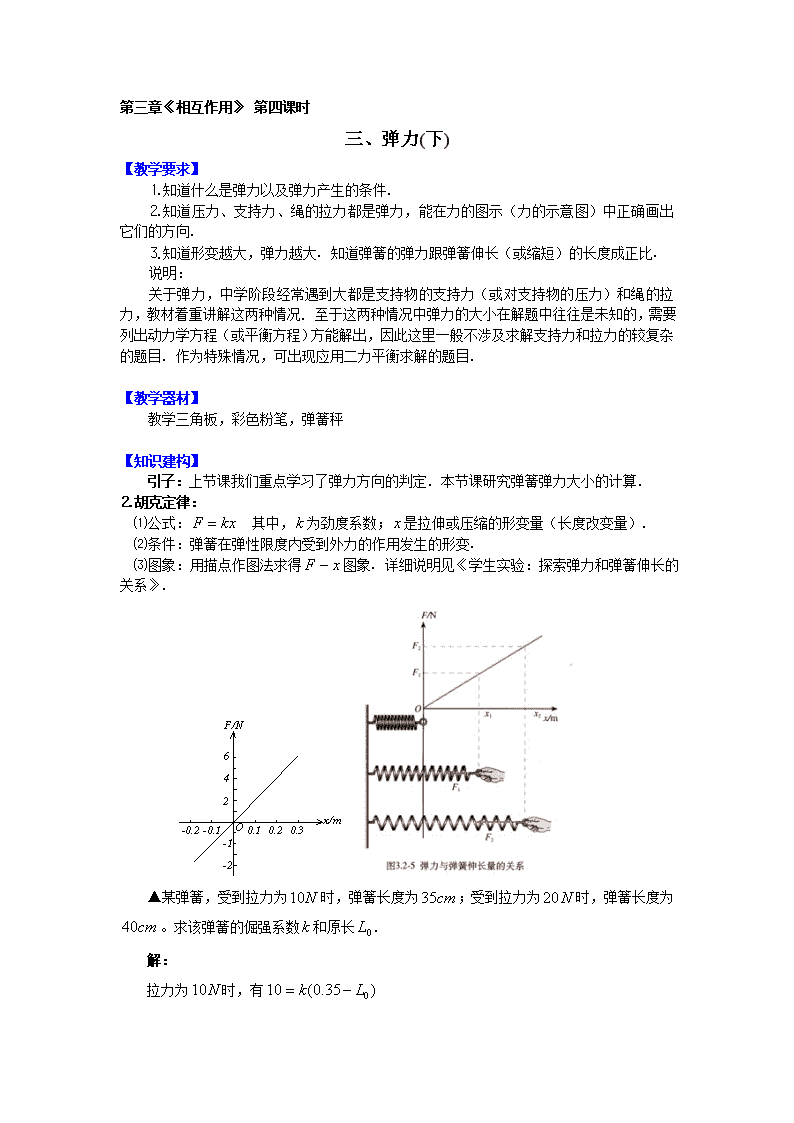
第三章《相互作用》 第四课时 三、弹力(下)‎ ‎【教学要求】‎ ‎⒈知道什么是弹力以及弹力产生的条件. ‎ ‎⒉知道压力、支持力、绳的拉力都是弹力，能在力的图示（力的示意图）中正确画出它们的方向. ‎ ‎⒊知道形变越大，弹力越大. 知道弹簧的弹力跟弹簧伸长（或缩短）的长度成正比. ‎ 说明：‎ 关于弹力，中学阶段经常遇到大都是支持物的支持力（或对支持物的压力）和绳的拉力，教材着重讲解这两种情况. 至于这两种情况中弹力的大小在解题中往往是未知的，需要列出动力学方程（或平衡方程）方能解出，因此这里一般不涉及求解支持力和拉力的较复杂的题目. 作为特殊情况，可出现应用二力平衡求解的题目. ‎ ‎【教学器材】‎ 教学三角板，彩色粉笔，弹簧秤 ‎【知识建构】‎ 引子：上节课我们重点学习了弹力方向的判定. 本节课研究弹簧弹力大小的计算. ‎ ‎⒉胡克定律：‎ ‎⑴公式： 其中，为劲度系数；是拉伸或压缩的形变量（长度改变量）. ‎ ‎⑵条件：弹簧在弹性限度内受到外力的作用发生的形变. ‎ ‎ ⑶图象：用描点作图法求得图象. 详细说明见《学生实验：探索弹力和弹簧伸长的关系》. ‎ ‎ ‎ ‎▲某弹簧，受到拉力为时，弹簧长度为；受到拉力为时，弹簧长度为。求该弹簧的倔强系数和原长. ‎ 解：‎ 拉力为时，有 拉力为时，有 故解得：‎ ‎▲某弹簧秤，不挂重物时，示数为；挂重物时，示数为（仍在弹性限度范围之内），则当示数为时，所挂物体的实际重力为多少？‎ 解：据胡克定律有： ，即；解得：‎ ‎▲如图，大弹簧比小弹簧长米，当压缩此组合弹簧（弹簧组）时，测得图象图如图所示，求两个弹簧的劲度系数和. ‎ 解：根据坐标点来列方程 ‎ ‎ ‎ ‎ 即： ‎ 点拔：关键是深刻理解：“在弹性限度范围内，弹簧的形变量与所受外力成正比”. ‎ ‎▲如图所示，A、B是两个相同的轻弹簧，原长，劲度系数，如果图中悬挂的两个物体质量均为，则两个弹簧的总长度为( )‎ ‎ A．22 cm B．24 cm C．26 cm D．28 cm ‎ 答案：略. ‎ ‎【课后思考】‎ ‎⒈判断：在轻绳下吊一个小铁球，则球对绳的拉力是绳子形变产生的吗？‎ 答案：不是；而是铁球形变产生的. ‎ 点评：物体的形变方向与这个形变产生的弹力方向相同；物体的形变方向与引起这个形 变的外力方向相反。即：‎ 练习：光滑平面，球压缩弹簧的过程中，弹簧对球的力使球减速，此力是弹簧发生形变而产生的。判断：‎ ‎ ⑴弹力的方向总与这个弹力的施力物体的弹性形变方向相反（√）‎ ‎ ⑵弹力的方向总与这个弹力的受力物体的弹性形变方向相同（√）‎ ‎ ⑶相互作用的两个弹力因其方向相反，故彼此产生形变方向也相反（√）‎ ‎【课后扩展】‎ 弹簧的等效劲度系数 ‎⒈并联弹簧的等效劲度系数 如下面左图所示，设有根劲度系数为的相同弹簧并在一起，两端受拉力时，每根弹簧的伸长量均为：. ‎ ‎ ‎ ‎ 把这根弹簧的并联组合看成一根弹簧，受同样拉力伸长同样长度时，则 所以，根相同弹簧并联的等效劲度系数为,即增大为一根弹簧的倍．‎ ‎⒉串联弹簧的等效劲度系数 如上面右图所示，设有根劲度系数为的相同弹簧串联在一起，受拉力时，每根弹簧的弹力均为，伸长量均为，根弹簧的总伸长量为 ‎ 把这根弹簧的串联组合看成一根弹簧，受同样拉力伸长同样长度时，则 ‎ 所以，根相同弹簧串联的等效劲度系数为 劲度系数()的决定因素 ‎ 劲度系数不同于比热、密度等反映物质特性的物理量，它反映的是某根具体弹簧的力学特性．‎ ‎ 研究表明，物体受到外力作用发生伸长形变时，由于内部各质点的相对位置发生变化，各质点间会 产生附加内力，即弹力()．单位面积上的内力跟相对伸长()成正比，即 或表示为. ‎ 这个关系称为胡克定律．式中由材料性质决定的量，称为弹性模量. ‎ 变换上式，得发生伸长形变时的弹力，式中称为劲度系数. 它不仅跟材料有关，还跟材料的横截面积和原长有关. 因此，一根弹簧被截成几段，由于原长不同，每段的值会发生变化.‎ 结语：前面我们着重学习了弹簧弹力的大小计算，注意：关键是深刻理解：“在弹性限度范围内，弹簧的形变量与所受外力成正比”。‎