【物理】2020届一轮复习人教版瞬时加速度问题和动力学图象问题课时作业 4页

‎　瞬时加速度问题和动力学图象问题 一、选择题(1～4为单项选择题，5为多项选择题)‎ ‎1.质量均为m的A、B两球之间连有一轻弹簧，放在光滑的水平台面上，A球紧靠墙壁，如图1所示．今用力F将B球向左推压弹簧，静止后，突然将力F撤去的瞬间(　　)‎ 图1‎ A．A的加速度大小为 B．A的加速度为零 C．B的加速度大小为 D．B的加速度大小为 答案　B 解析　撤去F之前，B球水平方向受到推力F和弹簧的弹力作用，处于静止状态，有：F＝F弹 A球受到弹簧向左的弹力和墙壁向右的支持力处于静止状态．F撤去瞬间，弹簧弹力不变，所以A球受力不变，合力仍然为零，加速度为零，A错误，B正确；对于B球，此时水平方向只受到弹簧向右的弹力，所以加速度a＝，C、D错误．‎ ‎2．如图2所示，A、B两木块间连一轻弹簧，A、B质量相等，一起静止地放在一块光滑木板上，若将此木板突然抽去，在此瞬间，A、B两木块的加速度分别是(　　)‎ 图2‎ A．aA＝0，aB＝2g B．aA＝g，aB＝g C．aA＝0，aB＝0‎ D．aA＝g，aB＝2g 答案　A 解析　抽出板后，A的受力情况未变，故A的加速度为0，木板对B的支持力消失，B受到弹簧向下的压力FN＝mg和重力，故aB＝＝＝2g.‎ ‎3．如图3所示，质量为m的小球用水平轻弹簧系住，并用倾角为30°的光滑木板AB托住，小球恰好处于静止状态．当木板AB突然向下撤离的瞬间，小球的加速度大小为(　　)‎ 图3‎ A．0 B.g C．g D.g 答案　B 解析　撤去木板后，小球受到的重力和弹簧的拉力不变，则 由牛顿第二定律＝ma，‎ 得：a＝＝g.‎ ‎4.质量为2 kg的物体在水平推力F的作用下沿水平面做直线运动，一段时间后撤去F，其运动的vt图象如图4所示．取g＝10 m/s2，则物体与水平面间的动摩擦因数μ和水平推力F的大小分别为(　　)‎ 图4‎ A．0.2,6 N B．0.1,6 N C．0.2,8 N D．0.1,8 N 答案　A 解析　在6～10 s内物体水平方向只受滑动摩擦力作用，加速度a＝－μg，vt图象的斜率表示加速度，a＝ m/s2＝－2 m/s2，解得μ＝0.2.在0～6 s内，F－μmg＝ma′，而a′＝‎ m/s2＝1 m/s2，解得F＝6 N．选项A正确．‎ ‎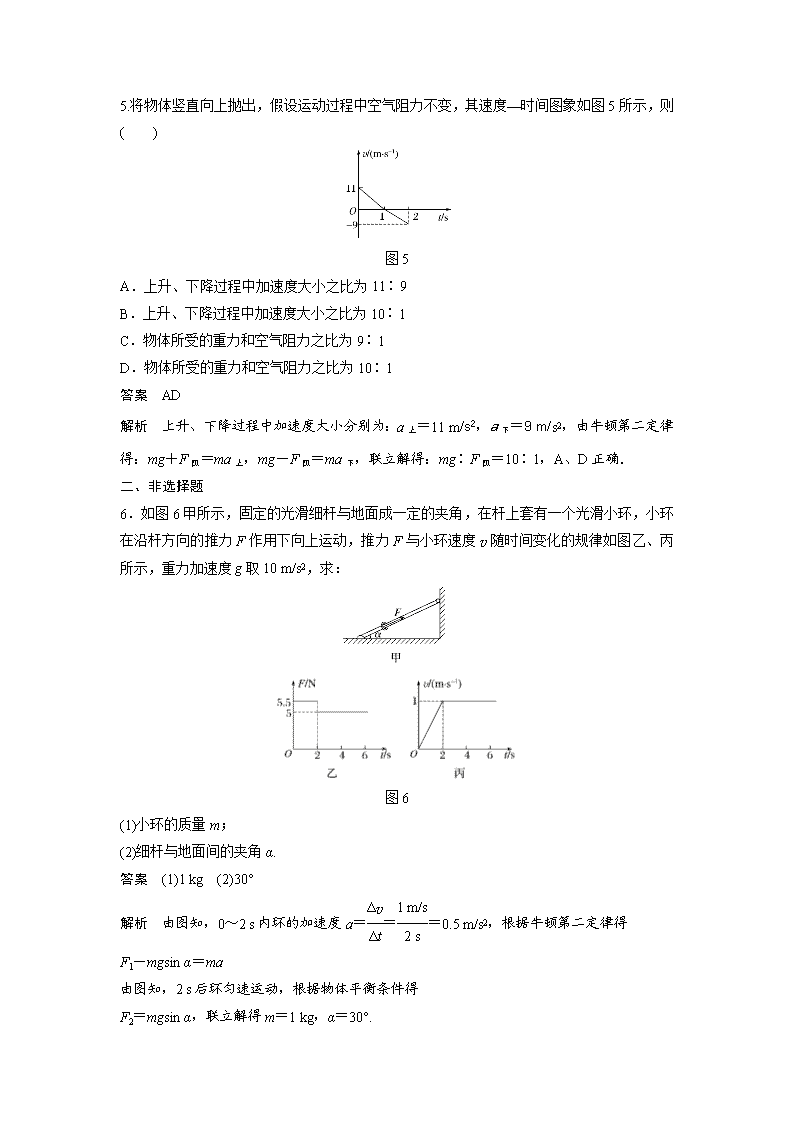5.将物体竖直向上抛出，假设运动过程中空气阻力不变，其速度—时间图象如图5所示，则(　　)‎ 图5‎ A．上升、下降过程中加速度大小之比为11∶9‎ B．上升、下降过程中加速度大小之比为10∶1‎ C．物体所受的重力和空气阻力之比为9∶1‎ D．物体所受的重力和空气阻力之比为10∶1‎ 答案　AD 解析　上升、下降过程中加速度大小分别为：a上＝11 m/s2，a下＝9 m/s2，由牛顿第二定律得：mg＋F阻＝ma上，mg－F阻＝ma下，联立解得：mg∶F阻＝10∶1，A、D正确．‎ 二、非选择题 ‎6．如图6甲所示，固定的光滑细杆与地面成一定的夹角，在杆上套有一个光滑小环，小环在沿杆方向的推力F作用下向上运动，推力F与小环速度v随时间变化的规律如图乙、丙所示，重力加速度g取10 m/s2，求：‎ 图6‎ ‎(1)小环的质量m；‎ ‎(2)细杆与地面间的夹角α.‎ 答案　(1)1 kg　(2)30°‎ 解析　由图知，0～2 s内环的加速度a＝＝＝0.5 m/s2，根据牛顿第二定律得 F1－mgsin α＝ma 由图知，2 s后环匀速运动，根据物体平衡条件得 F2＝mgsin α，联立解得m＝1 kg，α＝30°.‎ ‎7．如图7甲所示，倾角为θ＝37°的足够长斜面上，质量m＝1 kg的小物体在沿斜面向上的拉力F＝14 N作用下，由斜面底端从静止开始运动，2 s后撤去F，前2 s内物体运动的v-t 图象如图乙所示．求：(取g＝10 m/s2，sin 37°＝0.6，cos 37°＝0.8)‎ 图7‎ ‎(1)小物体与斜面间的动摩擦因数；‎ ‎(2)撤去力F后1.8 s时间内小物体的位移．‎ 答案　(1)0.5　(2)2.2 m，沿斜面向上 解析　(1)由题图乙可知，0～2 s内物体的加速度a1＝＝4 m/s2‎ 根据牛顿第二定律，F－mgsin θ－Ff＝ma1，‎ FN＝mgcos θ，而Ff＝μFN，代入数据解得μ＝0.5.‎ ‎(2)撤去F后，－mgsin θ－Ff＝ma2，得a2＝－10 m/s2，‎ 设经过t2时间减速到0，根据运动学公式0＝v1＋a2t2，‎ 解得t2＝0.8 s 在0.8 s内物体有向上运动的位移x2‎ ‎0－v＝2a2x2，得x2＝3.2 m 物体到最高点后向下运动，设加速度大小为a3，则 mgsin θ－Ff＝ma3，解得a3＝2 m/s2‎ 再经t3＝1 s物体发生位移x3，x3＝a3t＝1 m 物体在撤去F后1.8 s内的位移x＝x2－x3‎ 代入数据解得x＝2.2 m，方向沿斜面向上．‎