2013届高考物理第一轮复习备考演练试题22 7页

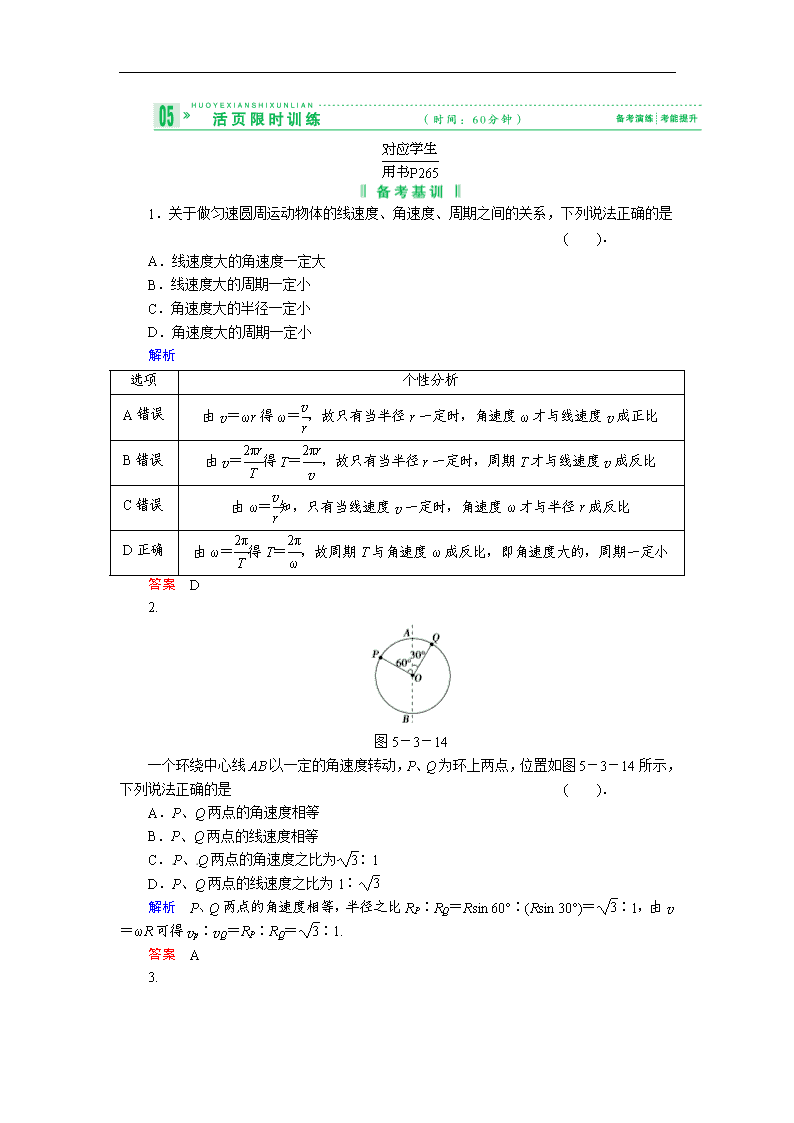
‎1．关于做匀速圆周运动物体的线速度、角速度、周期之间的关系，下列说法正确的是 ‎ (　　)．‎ A．线速度大的角速度一定大 B．线速度大的周期一定小 C．角速度大的半径一定小 D．角速度大的周期一定小 解析　‎ 选项 个性分析 A错误 由v＝ωr得ω＝，故只有当半径r一定时，角速度ω才与线速度v成正比 B错误 由v＝得T＝，故只有当半径r一定时，周期T才与线速度v成反比 C错误 由ω＝知，只有当线速度v一定时，角速度ω才与半径r成反比 D正确 由ω＝得T＝，故周期T与角速度ω成反比，即角速度大的，周期一定小 答案　D ‎2.‎ 图5－3－14‎ 一个环绕中心线AB以一定的角速度转动，P、Q为环上两点，位置如图5－3－14所示，下列说法正确的是 (　　)．‎ A．P、Q两点的角速度相等 B．P、Q两点的线速度相等 C．P、Q两点的角速度之比为∶1‎ D．P、Q两点的线速度之比为1∶ 解析　P、Q两点的角速度相等，半径之比RP∶RQ＝Rsin 60°∶(Rsin 30°)＝∶1，由v＝ωR可得vp∶vQ＝RP∶RQ＝∶1.‎ 答案　A ‎3.‎ 图5－3－15‎ 如图5－3－15所示，两个质量不同的小球用长度不等的细线拴在同一点，并在同一水平面内做匀速圆周运动，则它们的 (　　)．‎ ‎①周期相同　②线速度的大小相等　③角速度的大小相等　④向心加速度的大小相等 A．①② B．③④ ‎ C．①③ D．②④‎ 解析　设圆锥摆的高为h，则mg·＝m＝mω2r＝m2r＝ma，故v＝r ，ω＝ ，T＝2π ，a＝g.因两圆锥摆的h相同，而r不同，故两小球运动的线速度不同，角速度的大小相等，周期相同，向心加速度不同．‎ 答案　C ‎4.‎ 图5－3－16‎ ‎(2011·东北地区名校联考)如图5－3－16所示，质量为m的小球在竖直平面内的光滑圆环轨道上做圆周运动．圆环半径为R，小球经过圆环最高点时刚好不脱离圆环，则其通过最高点时 (　　)．‎ A．小球对圆环的压力大小等于mg B．小球受到的向心力等于0‎ C．小球的线速度大小等于 D．小球的向心加速度大小等于0‎ 解析　小球在最高点时刚好不脱离圆环，则圆环刚好对小球没有作用力，小球只受重力，重力竖直向下提供向心力，根据牛顿第二定律得小球的向心加速度大小为a＝＝g，再根据圆周运动规律得a＝＝g，解得v＝.(“绳”模型)‎ 答案　C ‎5．全国铁路大面积提速后，京哈、京沪、京广、胶济等提速干线的部分区段时速可达300公里，我们从济南到青岛乘“和谐号”列车就可以体验时速300公里的追风感觉．火车转弯可以看成是在水平面内做匀速圆周运动，火车速度提高会使外轨受损．为解决火车高速转弯时外轨受损这一难题，以下措施可行的是 (　　)．‎ A．适当减小内外轨的高度差 B．适当增加内外轨的高度差 C．适当减小弯道半径 D．以上说法都不可行 解析　设火车轨道平面的倾角为α时，火车转弯时内、外轨均不受损，根据牛顿第二定律有mgtan α＝m，解得v＝，所以为解决火车高速转弯时外轨受损这一难题，可行的措施是适当增加内外轨的高度差(即适当增大角α)和适当增大弯道半径r.‎ 答案　B ‎6．“天宫一号”目标飞行器经过我国科技工作者的不懈努力，终于在‎2011年9月29日晚21点16分发射升空．等待与神舟八号、九号、十号飞船对接．“天宫一号”在空中运行时，沿曲线从M点向N点飞行的过程中，速度逐渐减小，在此过程中“天宫一号”所受合力可能是下图中的(　　)．‎ 解析　‎ 答案　C ‎7．(2011·烟台模拟)关于匀速圆周运动的物体所受的向心力下列说法正确的是(　　)．‎ A．因向心力总是沿半径指向圆心，且大小不变，故向心力是一个恒力 B．因向心力指向圆心，且与线速度方向垂直，所以它不能改变线速度的大小 C．物体所受的合力不一定指向圆心 D．向心力和向心加速度的方向都是不变的 解析　做匀速圆周运动的物体所受的向心力是物体所受的合力，由于指向圆心，且与线速度垂直，不能改变线速度的大小，只能改变线速度的方向．向心力虽大小不变，但方向时刻改变，不是恒力，由此产生的向心加速度也是变化的，所以A、D、C错误，B正确．‎ 答案　B ‎8.‎ 图5－3－17‎ 如图5－3－17所示，一小球用细绳悬挂于O点，将其拉离竖直位置一个角度后释放，则小球以O点为圆心做圆周运动，运动中小球所需的向心力是(　　)．‎ A．绳的拉力 B．重力和绳的拉力的合力 C．重力和绳的拉力的合力沿绳方向的分力 D．以上说法都不对 解析　‎ 如图所示，对小球进行受力分析，它受重力和绳子拉力作用，向心力是指向圆心方向的合外力．因此，可以说是小球所受合力沿绳方向的分力，也可以是各力沿绳方向的分力的合力，C正确．‎ 答案　C ‎9.‎ 图5－3－18‎ 如图5－3－18两段长均为L的轻质线共同系住一个质量为m的小球，另一端分别固定在等高的A、B两点，A、B两点间距也为L，今使小球在竖直平面内做圆周运动，当小球到达最高点时速率为v，两段线中张力恰好均为零，若小球到达最高点时速率为2v，则此时每段线中张力大小为(　　)．‎ A.mg B．2mg ‎ C．3mg D．4mg 解析　‎ 当小球到达最高点速率为v，有mg＝m，当小球到达最高点速率为2v时，应有F＋mg＝m＝4mg，所以F＝3mg，此时最高点各力如图所示，所以FT＝mg，A正确．[来源:学§科§网Z§X§X§K]‎ 答案　A ‎10．汽车甲和汽车乙质量相等，以相等速率沿同一水平弯道做匀速圆周运动，甲车在乙车的外侧．两车沿半径方向受到的摩擦力分别为f甲和f乙．以下说法正确的是(　　)．‎ A．f甲小于f乙 B．f甲等于f乙 C．f甲大于f乙 D．f甲和f乙大小均与汽车速率无关 解析　根据题中的条件可知，两车在水平面做匀速圆周运动，则地面对车的摩擦力用来提供其做圆周运动的向心力，则F向＝f，又有向心力的表达式F向＝，因为两车的质量相同，两车运行的速率相同，因此轨道半径大的车所需的向心力小，即摩擦力小，A正确．‎ 答案　A ‎11.‎ 图5－3－19[来源:学科网]‎ 如图5－3－19所示，螺旋形光滑轨道竖直放置，P、Q为对应的轨道最高点，一个小球以一定速度沿轨道切线方向进入轨道，且能过轨道最高点P，则下列说法中正确的是(　　)．‎ A．轨道对小球做正功，小球的线速度vP>vQ B．轨道对小球不做功，小球的角速度ωP<ωQ C．小球的向心加速度aP>aQ[来源:学科网ZXXK]‎ D．轨道对小球的压力FP>FQ 解析　本题考查圆周运动和机械能守恒，中档题．轨道光滑，小球在运动的过程中只受重力和支持力，支持力时刻与运动方向垂直所以不做功，A错；那么在整个过程中只有重力做功满足机械能守恒，根据机械能守恒有vPrQ，根据ω＝，a＝，得小球在P点的角速度小于在Q点的角速度，B正确；在P点的向心加速度小于在Q点的向心加速度，C错；小球在P和Q两点的向心力由重力和支持力提供，即mg＋FN＝ma向，可得P点对小球的支持力小于Q点对小球的支持力，D错．‎ 答案　B ‎12.‎ 图5－3－20‎ 乘坐游乐园的过山车时，质量为m的人随车在竖直平面内沿圆周轨道运动(如图5－3－20所示)，下列说法正确的是(　　)．‎ A．车在最高点时，人处于倒坐状态，全靠保险带拉住，若没有保险带，人一定会掉下去 B．人在最高点时，对座位仍可能产生压力，但压力一定小于mg C．人在最低点时，处于矢重状态 D．人在最低点时，对座位的压力大于mg 解析　人在最高点如果速度较大，就会产生对座位的压力．并且压力也有可能大于mg而不致于掉落，故A、B均错；人在最低点时具有向上的加速度，因此处于超重状态，C对；在最低点满足FN＝mg＋m>mg，D对．‎ 答案　D ‎13.‎ 图5－3－21‎ 如图5－3－21所示，将完全相同的两小球A、B，用长L＝‎0.8 m的细绳悬于以v＝‎4 m/s向左匀速运动的小车顶部，两球与小车前后壁接触．由于某种原因，小车突然停止，此时悬线中张力之比FA∶FB为(g＝‎10 m/s2)(　　)．‎ A．1∶1 B．1∶2 ‎ C．1∶3 D．1∶4‎ 解析　小车突然停止，B球将做圆周运动，所以FB＝m＋mg＝‎30m；A球做水平方向减速运动，FA＝mg＝‎10 m，故此时悬线中张力之比为FA∶FB＝1∶3，C选项正确．‎ 答案　C ‎14．如图5－3－22甲所示，弯曲部分AB和CD是两个半径相等的圆弧，中间的BC段是竖直的薄壁细圆管(细圆管内径略大于小球的直径)，分别与上下圆弧轨道相切连接，BC段的长度L可作伸缩调节．下圆弧轨道与地面相切，其中D、A分别是上下圆弧轨道的最高点与最低点，整个轨道固定在竖直平面内．一小球多次以某一速度从A点水平进入轨道而从D点水平飞出．今在A、D两点各放一个压力传感器，测试小球对轨道A、D两点的压力，计算出压力差ΔF.改变BC的长度L，重复上述实验，最后绘得的ΔF－L图象如图5－3－22乙所示．(不计一切摩擦阻力，g取‎10 m/s2)‎ 图5－3－22‎ ‎(1)某一次调节后，D点的离地高度为‎0.8 m，小球从D点飞出，落地点与D点的水平距离为‎2.4 m，求小球经过D点时的速度大小；‎ ‎(2)求小球的质量和弯曲圆弧轨道的半径．[来源:学科网ZXXK]‎ 解析　(1)小球在竖直方向做自由落体运动，有：HD＝gt2，‎ 在水平方向做匀速直线运动，有：x＝vDt，‎ 得：vD＝＝＝‎6 m/s.‎ ‎(2)设轨道半径为r，A到D过程机械能守恒，有：‎ mvA2＝mvD2＋mg(2r＋L)， ①‎ 在A点：FA－mg＝m， ②‎ 在D点：FD＋mg＝m， ③‎ 由①②③式得：ΔF＝FA－FD＝6mg＋2mg，‎ 由图象纵截距得：6mg＝12 N，得m＝‎0.2 kg，‎ 当L＝‎0.5 m时，ΔF＝17 N，解得：r＝‎0.4 m．(“杆”模型)‎ 答案　(1)‎6 m/s　(2)‎0.2 kg　‎‎0.4 m