2020届二轮复习专题一第3讲力学中的曲线运动课件（64张） 64页

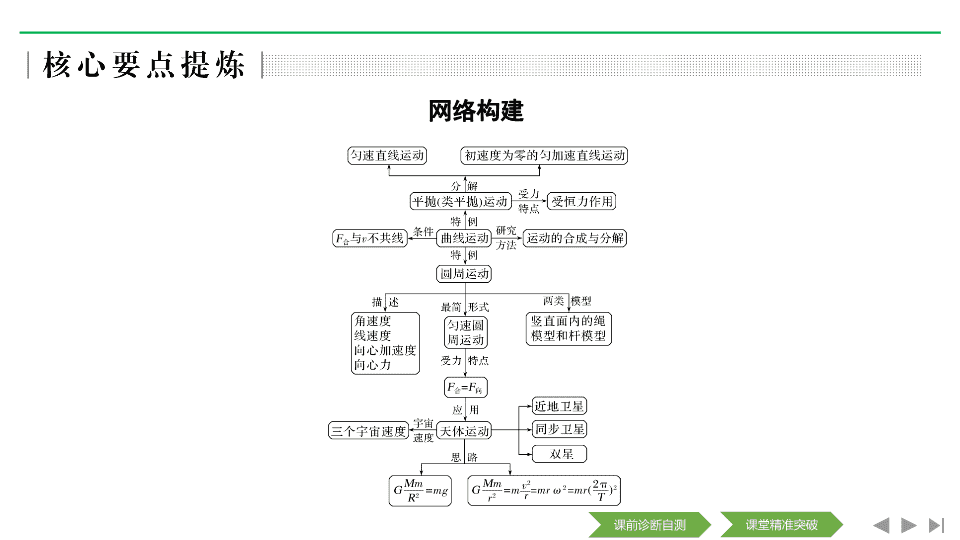
第 3 讲　力学中的曲线运动 网络构建 备考策略 1 . 必须领会的 “ 四种物理思想和三种常用方法 ” (1) 分解思想、临界极值的思想、估算的思想、模型化思想。 (2) 假设法、合成法、正交分解法。 2 . 平抛 ( 或类平抛 ) 运动的推论 (1) 任意时刻速度的反向延长线一定通过此时水平位移的中点。 (2) 设在任意时刻瞬时速度与水平方向的夹角为 θ ，位移与水平方向的夹角为 φ ，则有 tan θ ＝ 2tan φ 。 3 . 注意天体运动的三个区别 (1) 中心天体和环绕天体的区别。 (2) 自转周期和公转周期的区别。 (3) 星球半径和轨道半径的区别。 4 . 记住天体运动中的 “ 三看 ” 和 “ 三想 ” (1) 看到 “ 近地卫星 ” 想到 “ 最大绕行速度 ”“ 最小周期 ” 。 (2) 看到 “ 忽略地球自转 ” 想到 “ 万有引力等于重力 ” 。 (3) 看到 “ 同步卫星 ” 想到 “ 周期 T ＝ 24 h ” 。 运动的合成与分解及平抛运动 运动的合成与分解 图 1 (1) 从 A 点静止释放的小球，能落在第一台阶 M 1 N 1 上，则 l 至少应为多少个 h ； (2) 若小球由 P 点静止释放，经过 B 点时对轨道的压力为重力的 1.8 倍，令 ∠ BOP ＝ α ，求 α 大小 ( 已知 sin 37° ＝ 0.6 ， cos 37° ＝ 0.8) ； (3) 调整小球释放的位置，若使落在台阶 M 1 N 1 中点弹起后，恰好又落到 M 2 N 2 的中点，求从弹起到落回所经过的时间 t 及台阶宽度 l 与高度差 h 之间的关系。 (3) 小球落在台阶 M 1 N 1 时竖直速度为 在竖直方向上，选向下为正方向，设小球从 M 1 N 1 上弹起后落到 M 2 N 2 上所用的时间为 t 以 “ 体育运动 ” 中的网球为载体考查平抛运动的规律 【典例 2 】 (2019· 桐乡一中模拟 ) 如图 2 所示，是网球比赛场地图，单打区域长 MP 为 a ，宽 MN 为 b ，发球线到网的距离为 c ，一个球员在练习发球时，站在发球线的中点发球，将球打到对方左下方死角 ( 单打边线与底线的交点 ) ，若击球点的高度为 h ，网球被发出后做平抛运动 ( 球可看做质点，不计空气的阻力 ) ，重力加速度为 g 。则下列说法正确的是 ( 　　 ) 图 2 答案　 C 斜面上的平抛运动 【典例 3 】 (2019· 浙江乐清上学期高三模拟 ) ( 多选 ) 如图 3 所示，固定斜面 PO 、 QO 与水平面 MN 的夹角均为 45° ，现由 A 点分别以 v 1 、 v 2 先后沿水平方向抛出两个小球 ( 可视为质点 ) ，不计空气阻力，其中以 v 1 抛出的小球恰能垂直于 QO 落于 C 点，飞行时间为 t ，以 v 2 抛出的小球落在 PO 斜面上的 B 点，且 B 、 C 在同一水平面上，重力加速度大小为 g ，则 ( 　　 ) 图 3 解析　 落于 C 点的小球速度垂直 QO ，则分解速度，如图所示，则 v 1 ＝ gt ，水平位移 x ＝ v 1 t ＝ gt 2 ，选项 C 正确；落于 B 点的小球，则分解位移如图所示。 其中， BC 在同一平面，下落高度相同，故飞行时间都为 t ， 答案　 ACD 【典例 4 】 (2019· 浙江桐乡高级中学高三模拟 ) 甲、乙两个同学对打乒乓球，设甲同学持拍的拍面与水平方向成 α 角，乙同学持拍的拍面与水平方向成 β 角，如图 4 所示，设乒乓球击打拍面时速度与拍面垂直，且乒乓球每次击打球拍前与击打后速度大小相等，不计空气阻力，则乒乓球击打甲的球拍的速度 v 1 与乒乓球击打乙的球拍的速度 v 2 之比为 ( 　　 ) 图 4 答案　 A 1. (2019· 杭州高三模拟 ) 乒乓球发球机是一个很好的辅助练习者练球的工具。如图 5 甲所示，是乒乓球发球机的实物图，图乙是简化示意图。设乒乓球桌面 ABCD 的 AB 边长为 L 1 ， BC 边长为 L 2 ，球网 JK 位于桌面的正中间，网高为 h ；发球机简化为 EF ，其中 E 点固定在 AB 边的中点， F 点为乒乓球发射点， EF 始终保持竖直，高度为 H ( 可调 ) 。乒乓球看成质点，每次均从 F 点水平发射，发射方向可以在水平面内任意调整，不计空气阻力和周围环境对乒乓球运动的影响，若球擦网而过时不计球和网之间的相互作用，不考虑乒乓球的旋转，重力加速度大小为 g ，则下列说法正确的是 ( 　　 ) 图 5 答案　 D 2. (2019· 浙江余姚选考模拟 ) ( 多选 ) 如图 6 所示，水平面内放置一个直径 d ＝ 1 m ，高 h ＝ 1 m 的无盖薄油桶，沿油桶直径距左桶壁 s ＝ 2 m 处的正上方有一点 P ， P 点的高度 H ＝ 3 m ，从 P 点沿直径方向水平抛出一小球，不考虑小球的反弹，下列说法正确的是 ( 取 g ＝ 10 m/s 2 )( 　　 ) 图 6 答案　 ACD 3. (2019· 绍兴市期末 ) 某学生在台阶上玩玻璃弹子。他在平台最高处将一个小玻璃弹子垂直于棱角边推出，以观察弹子的落点位置。台阶的尺寸如图 7 所示，高 a ＝ 0.2 m ，宽 b ＝ 0.3 m ，不计空气阻力。 ( g 取 10 m/s 2 ) 图 7 (1) 要使弹子落在第一级台阶上，推出的速度 v 1 应满足什么条件？ (2) 若弹子被水平推出的速度 v 2 ＝ 4 m/s ，它将落在第几级台阶上？ 解析　 (1) 显然 v 1 不能太大，考虑临界状况 ( 落在尖角处 ) (2) 构造由题图中尖角所成的斜面，建立坐标系 分析知，玻璃弹子将落在第 8 级台阶上。 答案　 (1) v 1 ≤ 1.5 m/s 　 (2)8 【典例 1 】 (2019· 浙江杭州上学期高三模拟 ) 游乐园的小型 “ 摩天轮 ” 上对称站着质量均为 m 的 8 位同学。如图 8 所示， “ 摩天轮 ” 在竖直平面内逆时针匀速转动，若某时刻转到顶点 a 上的甲同学让一小重物做自由落体运动 ( 忽略重物刚掉落时水平运动的影响 ) ，并立即通知下面的同学接住，结果重物掉落时正处在 c 处 ( 如图 ) 的乙同学恰好在第一次到达最低点 b 处时接到，已知 “ 摩天轮 ” 半径为 R ，重力加速度为 g ( 人和吊篮的大小及重物的质量可忽略 ) 。求： 图 8 圆周运动问题 圆周运动的运动学及动力学问题 (1) 接住前重物下落的时间 t ； (2) 人和吊篮随 “ 摩天轮 ” 运动的线速度 v 的大小； (3) 乙同学在最低点处对地板的压力 F N 。 平抛运动与圆周运动的组合问题 【典例 2 】 (2017· 全国卷 Ⅱ ， 17) 如图 9 ，半圆形光滑轨道固定在水平地面上，半圆的直径与地面垂直，一小物块以速度 v 从轨道下端滑入轨道，并从轨道上端水平飞出，小物块落地点到轨道下端的距离与轨道半径有关，此距离最大时，对应的轨道半径为 ( 重力加速度大小为 g )( 　　 ) 图 9 解析　 物块由最低点到最高点的过程，由机械能守恒定律得 物块做平抛运动时，落地点到轨道下端的距离 x ＝ v 1 t ， 答案　 B (1) 解决圆周运动问题要注意以下几点 ① 要进行受力分析，明确向心力的来源，确定圆心以及半径。 ② 列出正确的动力学方程 (2) 竖直平面内圆周运动的最高点和最低点的速度通常利用动能定理来建立联系，然后结合牛顿第二定律进行动力学分析。 　　　　 1. (2019· 浙江乐清选考模拟 ) ( 多选 ) 北京时间 2017 年 9 月 7 日，全运会在天津举办，山东队 28 岁的张成龙以 14.733 分在男子单杠决赛中获得第一名。假设张成龙训练时做 “ 单臂大回环 ” 的高难度动作时，用一只手抓住单杠，伸展身体，以单杠为轴做圆周运动。如图 10 甲所示，张成龙运动到最高点时，用力传感器测得张成龙与单杠间弹力大小为 F ，用速度传感器记录他在最高点的速度 ( 指他的重心的线速度 ) 大小为 v ，得到 F － v 2 图象如图乙所示。 g 取 10 m/s 2 ，则下列说法中正确的是 ( 　　 ) 图 10 A. 张成龙的质量为 65 kg B. 张成龙的重心到单杠的距离为 0.9 m C. 当张成龙在最高点的速度为 4 m/s 时，张成龙受单杠的弹力方向向上 D. 在完成 “ 单臂大回环 ” 的过程中，张成龙运动到最低点时，单臂最少要承受 3 250 N 的力 答案　 ABD 2. (2019· 浙江东阳中学高三上学期模拟 ) 如图 11 所示是磁带录音机的磁带盒的示意图， A 、 B 为缠绕磁带的两个轮子，其半径均为 r 。在放音结束时，磁带全部绕到了 B 轮上，磁带的外缘半径为 R ，且 R ＝ 3 r 。现在进行倒带，使磁带绕到 A 轮上。倒带时 A 轮是主动轮，其角速度是恒定的， B 轮是从动轮。经测定磁带全部绕到 A 轮上需要的时间为 t 。则从开始倒带到 A 、 B 两轮的角速度相等所需要的时间 ( 　　 ) 图 11 答案　 B 3. (2019· 浙江温州质检 ) ( 多选 ) 质量为 m 的小球由轻绳 a 和 b 分别系于一轻质细杆的 A 点和 B 点，如图 12 所示， a 绳与水平方向成 θ 角， b 绳沿水平方向且长为 l ，当轻杆绕轴 AB 以角速度 ω 匀速转动时， a 、 b 两绳均伸直，小球在水平面内做匀速圆周运动，则下列说法正确的是 ( 　　 ) 图 12 答案　 AD 4. (2019· 浙江舟山质检 ) 如图 13 所示是对质量为 m ＝ 0.1 kg 的某型号玩具小车性能进行测试的装置，它是由固定长度为 L ＝ 1.5 m 的粗糙直轨道 AB 、半径为 R ＝ 0.2 m 的光滑圆形轨道 BCB ′ 以及长度可调的粗糙直轨道 B ′ D 三部分平滑连接而成 ( BB ′ 略有错开 ) ，整个装置置于距地面足够高的水平平台上，轨道末端 D 始终与平台右端重合；为了保护小车安全，在距平台右端 x ＝ 0.9 m 处竖立一堵竖直泡沫墙 EP 。已知小车在 AB 、 B ′ D 上运动时所受阻力恒为车重的 0.2 倍，测试时小车从 A 点以恒定功率向 B 运动，到达 B 点时恰好达到最大速度，然后进入圆形轨道同时关闭小车动力。某次测试测得小车在通过圆形轨道最高点 C 时对轨道压力大小为 3.0 N ， g 取 10 m/s 2 。试求： 图 13 (1) 小车在通过 C 点时的速度大小； (2) 小车在 AB 段运动时的功率和运动时间； (3) 保持其他物理量不变，应调节 B ′ D 的长度为多大，小车才能以最小动能撞击泡沫墙 EP ？最小动能为多少？ 解析　 (1) 由牛顿第三定律知小车在圆形轨道最高点时，轨道对小车的作用力 F ＝ 3.0 N ，在最高点有 图 14 万有引力与天体的运动 开普勒三定律与万有引力定律的应用 答案　 A 【典例 2 】 (2019· 稽阳联谊学校联考 ) 国产科幻片《流浪地球》的成功上演，掀起了天体热。小明同学课外查阅太阳系行星的一些资料。太阳系各行星几乎在同一平面内沿同一方向绕太阳做圆周运动。当地球恰好运行到某地外行星和太阳之间，且三者几乎排成一条直线的现象，天文学称为 “ 行星冲日 ” 。据报道， 2014 年各行星冲日时间分别是： 1 月 6 日木星冲日； 4 月 9 日火星冲日； 5 月 11 日土星冲日； 8 月 29 日海王星冲日； 10 月 8 日天王星冲日。已知地球及各地外行星绕太阳运动的轨道半径如下表所示，则下列判断中正确的是 ( 　　 ) 轨道半径 (AU) 地球 火星 木星 土星 天王星 海王星 1.0 1.5 5.2 9.5 19 30 A. 各地外行星每年都会出现冲日现象 B. 在 2015 年内一定会出现木星冲日 C. 天王星相邻两次冲日的时间间隔为土星的一半 D. 地外行星中，海王星相邻两次冲日的时间间隔最长 答案　 B 天体质量、密度的估算 【典例 3 】 (2019· 桐乡一中高三年级周考 ) 2018 年 2 月，我国 500 m 口径射电望远镜 ( 天眼 ) 发现毫秒脉冲星 “ J0318 ＋ 0253 ” ，其自转周期 T ＝ 5.19 ms 。假设星体为质量均匀分布的球体，已知万有引力常量为 6.67 × 10 － 11 N·m 2 /kg 2 。以周期 T 稳定自转的星体的密度最小值约为 ( 　　 ) 图 15 A.5 × 10 9 kg/m 3 B.5 × 10 12 kg/m 3 C.5 × 10 15 kg/m 3 D.5 × 10 18 kg/m 3 答案　 C 卫星运行参量的分析 答案　 BC 卫星的变轨与对接 【典例 5 】 “ 嫦娥五号 ” 作为我国登月计划中第三期工程的 “ 主打星 ” ，登月后又从月球起飞，并以 “ 跳跃式返回技术 ” 成功返回地面，完成探月第三期工程的重大跨越带回月球样品。 “ 跳跃式返回技术 ” 是指航天器在关闭发动机后进入大气层，依靠大气升力再次冲出大气层，降低速度后进入大气层。如图 16 所示，虚线为大气层的边界，已知地球半径为 R ， d 点与地心距离为 r ，地球表面重力加速度为 g 。下列说法正确的是 ( 　　 ) 图 16 答案　 D 1 . 分析卫星轨道半径与运行参数关系应注意 卫星轨道半径越大，同一卫星所受万有引力越小，其线速度、角速度、向心加速度越小，周期越大；动能越小，势能越大，机械能越大。 2 . 天体运动与几何关系相结合问题 (1) 多星模型中分析天体的运行轨道半径与星体间距的关系。 (2) 求解传播时间、挡光时间时通常需作出轨迹圆的切线，分析边角关系。 　　　　 1. (2019· 浙江永康选考模拟 ) 如图 17 所示是嫦娥三号奔月过程中某阶段的运动示意图，嫦娥三号沿椭圆轨道 Ⅰ 运动到近月点 P 处变轨进入圆轨道 Ⅱ ，嫦娥三号在圆轨道 Ⅱ 做圆周运动的轨道半径为 r ，周期为 T ，已知引力常量为 G ，下列说法中正确的是 ( 　　 ) 图 17 A. 由题中 ( 含图中 ) 信息可求得月球的质量 B. 由题中 ( 含图中 ) 信息可求得月球第一宇宙速度 C. 嫦娥三号在 P 处变轨时必须点火加速 D. 嫦娥三号沿椭圆轨道 Ⅰ 运动到 P 处时的加速度大于沿圆轨道 Ⅱ 运动到 P 处时的加速度 答案　 A 2. (2019·4 月浙江选考， 7) 某颗北斗导航卫星属于地球静止轨道卫星 ( 即卫星相对于地面静止 ) 。则此卫星的 ( 　　 ) 图 18 A. 线速度大于第一宇宙速度 B. 周期小于同步卫星的周期 C. 角速度大于月球绕地球运行的角速度 D. 向心加速度大于地面的重力加速度 答案　 C 3. (2019· 浙江宁波重点中学高三联考 ) 2017 年 11 月 5 日我国在西昌卫星发射中心用长征三号乙运载火箭，以 “ 一箭双星 ” 方式成功发射了第 24 、 25 颗北斗导航卫星，开启了北斗卫星导航系统全球组网的新时代。北斗导航系统由 5 颗静止轨道卫星 ( 即卫星相对地面的位置保持不变 ) 和 30 颗非静止轨道卫星组成，其中北斗 G5 为地球静止轨道卫星，轨道高度约为 36 000 km ；北斗 M3 为中圆地球轨道卫星，轨道高度约为 21 500 km ，已知地球半径为 6 400 km ，则下列说法中正确的是 ( 　　 ) A. 北斗 G5 绕地球运转周期为 24 h B. 北斗 G5 绕地球运转的线速度大于 7.9 km/s C. 北斗 M3 绕地球运转的角速度小于北斗 G5 的角速度 D. 北斗 M3 绕地球运转的向心加速度小于北斗 G5 的向心加速度 答案　 A 4. (2019· 浙江金华选考模拟 ) ( 多选 ) 2017 年 4 月，我国第一艘货运飞船天舟一号顺利升空，随后与天宫二号对接。假设天舟一号从 B 点发射经过椭圆轨道运动到天宫二号所在的圆轨道上完成对接，如图 19 所示。已知天宫二号的轨道半径为 r ，天舟一号沿椭圆轨道运动的周期为 T ， A 、 B 两点分别为椭圆轨道的远地点和近地点，地球半径为 R ，引力常量为 G 。则下列说法正确的是 ( 　　 ) 图 19 A. 天宫二号的运行速度小于 7.9 km/s B. 天舟一号的发射速度大于 11.2 km/s C. 根据题中信息可以求出地球的质量 D. 天舟一号在 A 点的运行速度大于天宫二号在 A 点的运行速度 答案　 AC 热点模型构建 —— 常考的圆周运动模型 竖直平面的圆周运动 “ 绳、杆 ” 模型   绳模型 杆模型 常见类型 均是没有支撑的小球 均是有支撑的小球 【典例】 (2019· 宁波市新高考适应性考试 ) 如图 20 所示，竖直面内用光滑钢管弯成的 “9” 字形固定轨道与水平桌面的右端相接， “9” 字全高 H ＝ 0.8 m ， “9” 字上半部分四分之三圆弧半径为 R ＝ 0.2 m ，钢管的内径大小忽略不计。桌面左端固定轻质弹簧，开始弹簧处于锁定状态，其右端处于 A 位置，此时弹簧具有的弹性势能为 E p ＝ 2.16 J ，将质量 m ＝ 0.1 kg 的可看作质点的小球放在 A 位置与弹簧相接触，解除弹簧锁定后，小球从 A 被弹出后经过 B 点进入 “9” 字形轨道最后从 D 点水平抛出， AB 间水平距离为 L ＝ 1.2 m 小球与桌面间的动摩擦因数为 μ ＝ 0.3 ，重力加速度 g ＝ 10 m/s 2 ，不计空气阻力，试求： 图 20 (1) 弹簧解除锁定后，小球到 B 点时的速度大小； (2) 小球运动到轨道最高点 C 时对轨道的作用力； (3) 若小球从 “9” 字形轨道 D 点水平抛出后，第一次与地面碰撞前速度方向与水平地面倾角 θ ＝ 45° ，每一次与地面碰撞过程中小球水平速度分量保持不变，小球弹起来的竖直速度分量减小为碰撞前的一半，求小球第一次弹起后距地面的高度。 解析　 (1) 弹簧解除锁定后，由动能定理得 由牛顿第三定律，压力等于支持力，方向竖直向上。 答案　 (1)6 m/s 　 (2)9 N 　竖直向上　 (3)0.35 m