【物理】2020届一轮复习人教版探究弹簧形变与弹力的关系课时作业 2页

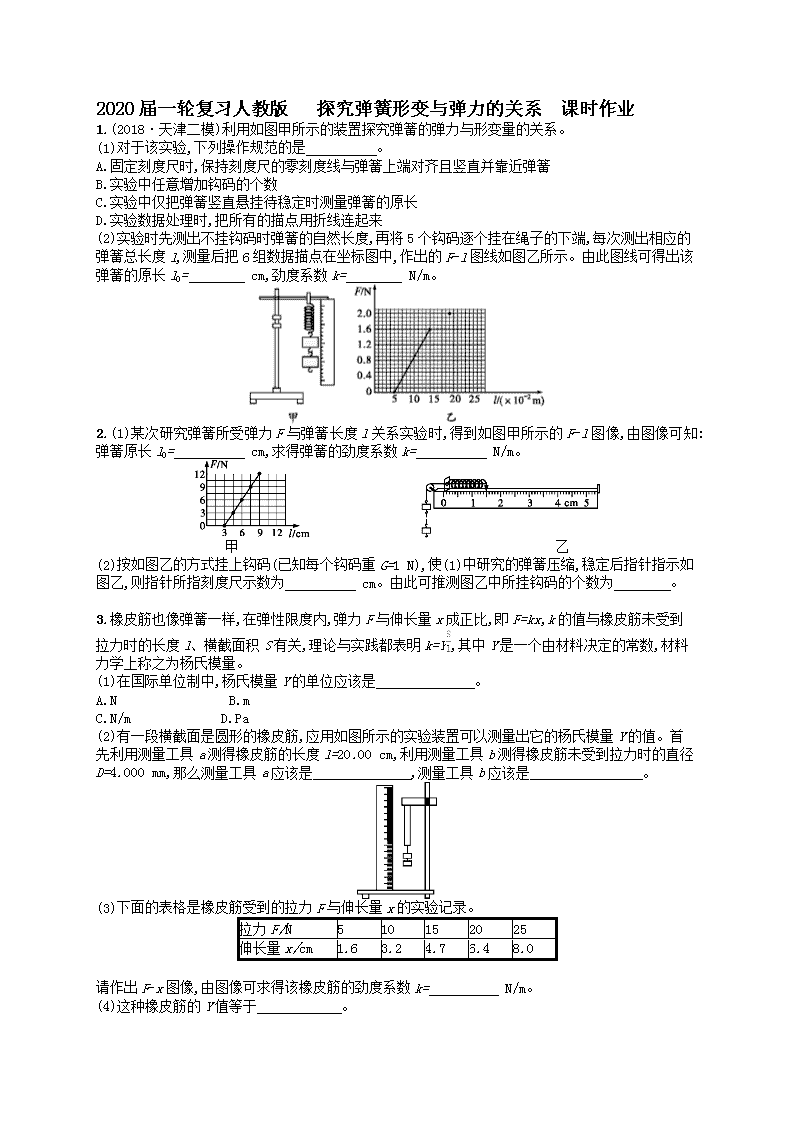
‎2020届一轮复习人教版 探究弹簧形变与弹力的关系 课时作业 ‎1.(2018·天津二模)利用如图甲所示的装置探究弹簧的弹力与形变量的关系。‎ ‎(1)对于该实验,下列操作规范的是　　　　　。 ‎ A.固定刻度尺时,保持刻度尺的零刻度线与弹簧上端对齐且竖直并靠近弹簧 B.实验中任意增加钩码的个数 C.实验中仅把弹簧竖直悬挂待稳定时测量弹簧的原长 D.实验数据处理时,把所有的描点用折线连起来 ‎(2)实验时先测出不挂钩码时弹簧的自然长度,再将5个钩码逐个挂在绳子的下端,每次测出相应的弹簧总长度l,测量后把6组数据描点在坐标图中,作出的F-l图线如图乙所示。由此图线可得出该弹簧的原长l0=　　　　 cm,劲度系数k=　　　　 N/m。 ‎ ‎2.(1)某次研究弹簧所受弹力F与弹簧长度l关系实验时,得到如图甲所示的F-l图像,由图像可知:弹簧原长l0=　　　　　 cm,求得弹簧的劲度系数k=　　　　　 N/m。 ‎ ‎ ‎ 甲 乙 ‎(2)按如图乙的方式挂上钩码(已知每个钩码重G=1 N),使(1)中研究的弹簧压缩,稳定后指针指示如图乙,则指针所指刻度尺示数为　　　　　 cm。由此可推测图乙中所挂钩码的个数为　　　　。 ‎ ‎3.橡皮筋也像弹簧一样,在弹性限度内,弹力F与伸长量x成正比,即F=kx,k的值与橡皮筋未受到拉力时的长度l、横截面积S有关,理论与实践都表明k=Y,其中Y是一个由材料决定的常数,材料力学上称之为杨氏模量。‎ ‎(1)在国际单位制中,杨氏模量Y的单位应该是　　　　　　　。 ‎ A.N　　　　　　　　B.m C.N/m D.Pa ‎(2)有一段横截面是圆形的橡皮筋,应用如图所示的实验装置可以测量出它的杨氏模量Y的值。首先利用测量工具a测得橡皮筋的长度l=20.00 cm,利用测量工具b测得橡皮筋未受到拉力时的直径D=4.000 mm,那么测量工具a应该是　　　　　　　,测量工具b应该是　　　　　　　　。 ‎ ‎(3)下面的表格是橡皮筋受到的拉力F与伸长量x的实验记录。‎ 拉力F/N ‎5‎ ‎10‎ ‎15‎ ‎20‎ ‎25‎ 伸长量x/cm ‎1.6‎ ‎3.2‎ ‎4.7‎ ‎6.4‎ ‎8.0‎ 请作出F-x图像,由图像可求得该橡皮筋的劲度系数k=　　　　　 N/m。 ‎ ‎(4)这种橡皮筋的Y值等于　　　　　　。 ‎ ‎8　探究弹簧形变与弹力的关系 ‎1.解析(1)固定刻度尺时,保持刻度尺的零刻度线与弹簧上端对齐且竖直并靠近弹簧,故A正确;实验过程应使弹簧始终在弹性限度内,实验中不能任意增加钩码的个数,以防止超过弹簧的劲度系数,故B错误;为防止弹簧自重对实验的影响,实验中仅把弹簧竖直悬挂待稳定时测量弹簧的原长,故C正确;实验数据处理时,应根据实验数据在坐标系内描出对应点,然后作出图像,图像应是直线而不是折线,故D错误。‎ ‎(2)由图示图像可知,F=0N时l=0.05m=5cm,则弹簧的原长为5cm,弹簧的劲度系数:k==20N/m。‎ 答案(1)AC　(2)5　20‎ ‎2.解析(1)由胡克定律F=k(l-l0),结合题图甲中数据得l0=3.0cm,k=200N/m。‎ ‎(2)由题图乙知指针所示刻度为1.50cm,由F=k(l0-l),可求得此时弹力为F=3N,故所挂钩码的个数为3。‎ 答案(1)3.0　200　(2)1.50　3‎ ‎3.解析(1)在弹性限度内,弹力F与伸长量x成正比,F=kx,由题意可知k=,则F=kx=Y·x,解得杨氏模量Y=,各物理量取国际单位得杨氏模量的单位是N/m2=Pa,选项D正确。‎ ‎(2)根据精度判断可知a为毫米刻度尺,b为螺旋测微器。‎ ‎(3)根据表格数据,描点、连线,可得F-x图像如图所示。根据斜率的物理意义表示劲度系数k,可知k=≈312.5N/m。‎ ‎(4)根据Y=求得,Y≈4.98×106Pa。‎ 答案(1)D　(2)毫米刻度尺　螺旋测微器　(3)见解析图　312.5　(4)4.98×106 Pa