河南省新乡市2017届高三（上）模拟物理试卷（解析版） 17页

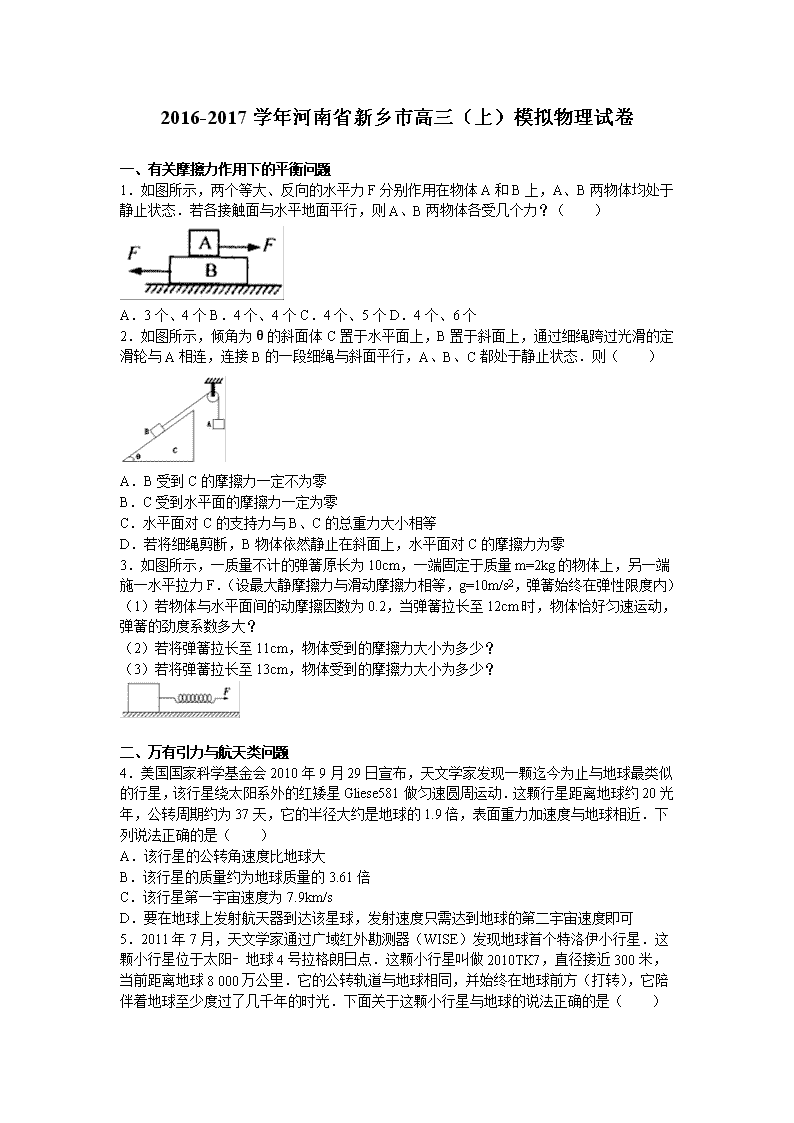
‎2016-2017学年河南省新乡市高三（上）模拟物理试卷 ‎　‎ 一、有关摩擦力作用下的平衡问题 ‎1．如图所示，两个等大、反向的水平力F分别作用在物体A和B上，A、B两物体均处于静止状态．若各接触面与水平地面平行，则A、B两物体各受几个力？（　　）‎ A．3个、4个B．4个、4个C．4个、5个D．4个、6个 ‎2．如图所示，倾角为θ的斜面体C置于水平面上，B置于斜面上，通过细绳跨过光滑的定滑轮与A相连，连接B的一段细绳与斜面平行，A、B、C都处于静止状态．则（　　）‎ A．B受到C的摩擦力一定不为零 B．C受到水平面的摩擦力一定为零 C．水平面对C的支持力与B、C的总重力大小相等 D．若将细绳剪断，B物体依然静止在斜面上，水平面对C的摩擦力为零 ‎3．如图所示，一质量不计的弹簧原长为10cm，一端固定于质量m=2kg的物体上，另一端施一水平拉力F．（设最大静摩擦力与滑动摩擦力相等，g=10m/s2，弹簧始终在弹性限度内）‎ ‎（1）若物体与水平面间的动摩擦因数为0.2，当弹簧拉长至12cm时，物体恰好匀速运动，弹簧的劲度系数多大？‎ ‎（2）若将弹簧拉长至11cm，物体受到的摩擦力大小为多少？‎ ‎（3）若将弹簧拉长至13cm，物体受到的摩擦力大小为多少？‎ ‎　‎ 二、万有引力与航天类问题 ‎4．美国国家科学基金会2010年9月29日宣布，天文学家发现一颗迄今为止与地球最类似的行星，该行星绕太阳系外的红矮星Gliese581做匀速圆周运动．这颗行星距离地球约20光年，公转周期约为37天，它的半径大约是地球的1.9倍，表面重力加速度与地球相近．下列说法正确的是（　　）‎ A．该行星的公转角速度比地球大 B．该行星的质量约为地球质量的3.61倍 C．该行星第一宇宙速度为7.9km/s D．要在地球上发射航天器到达该星球，发射速度只需达到地球的第二宇宙速度即可 ‎5．2011年7月，天文学家通过广域红外勘测器（WISE）发现地球首个特洛伊小行星．这颗小行星位于太阳﹣地球4号拉格朗日点．这颗小行星叫做2010TK7，直径接近300米，当前距离地球8 000万公里．它的公转轨道与地球相同，并始终在地球前方（打转），它陪伴着地球至少度过了几千年的时光．下面关于这颗小行星与地球的说法正确的是（　　）‎ A．绕太阳运动的向心加速度大小相等 B．受到太阳的万有引力大小相等 C．绕太阳运动的周期相等 D．在小行星运动一个周期过程中万有引力做正功 ‎6．（多）气象卫星可以测量气象数据，分为两类．我国先后自行成功研制和发射了“风云Ⅰ号”和“风云Ⅱ号”两颗气象卫星，“风云Ⅰ号”卫星轨道与赤道平面垂直并且通过两极，称为“极地圆轨道”，每12h巡视地球一周．“风云Ⅱ号”气象卫星轨道平面在赤道平面内，称为“地球同步轨道”，每24h巡视地球一周，则“风云Ⅰ号”卫星比“风云Ⅱ号”卫星（　　）‎ A．线速度大B．发射速度小C．万有引力小D．向心加速度大 ‎　‎ 三、传送带类问题 ‎7．如图所示，物体沿弧形轨道滑下后进入足够长的水平传送带，传送带以图示方向匀速运转，则传送带对物体做功情况可能是（　　）‎ A．始终不做功B．先做负功后做正功 C．先做正功后不做功D．先做负功后不做功 ‎8．在一水平向右匀速传输的传送带的左端A点，每隔T的时间，轻放上一个相同的工件，已知工件与传送带间动摩擦因素为μ，工件质量均为m，经测量，发现后面那些已经和传送带达到相同速度的工件之间的距离为x，下列判断正确的有（　　）‎ A．传送带的速度为 B．传送带的速度为2‎ C．每个工件与传送带间因摩擦而产生的热量为 D．在一段较长的时间t内，传送带因为传送工件而将多消耗的能量为 ‎9．一传送带装置示意图，其中传送带经过AB区域时是水平的，经过BC区域时变为圆弧形（圆弧由光滑模板形成，未画出），经过CD区域时是倾斜的，AB和CD都与BC相切．现将大量的质量均为m的小货箱一个一个在A处放到传送带上，放置时初速度为零，经传送带运送到D处，D和A的高度差为h．稳定工作时传送带速度不变，CD段上各箱等距排列，相邻两箱的距离为L．每个箱子在A处投放后，在到达B之前已经相对于传送带静止，且以后也不再滑动（忽略经BC段的微小滑动）．已知在一段相当长的时间T内，共运送小货箱的数目N个．这装置由电动机带动，传送带与轮子间无相对滑动，不计轮轴处的摩擦．求电动机的平均功率．‎ ‎　‎ 四、带电粒子在电场中的加速 ‎10．如图所示，A、B是一对中间有小孔的金属板，两小孔的连线与金属板面相垂直，两极板间的距离为L，两极板间加上低频交流电压，A板电势为零，B板电势为U=Uocosωt，现有一电子在t=0时刻从A板上的小孔进入电场，设初速度和重力的影响均可忽略不计，则电子在两极板间可能（　　）‎ A．以AB间的某一点为平衡位置来回振动 B．时而向B板运动，时而向A板运动，但最后穿出B板 C．一直向B板运动，最后穿出B板，如果ω小于某个值ωo，L小于某个值Lo D．一直向B板运动，最后穿出B板，而不论ω、L为何值 ‎11．如图1所示，两平行金属板竖直放置，左极板接地，中间有小孔．右极板电势随时间变化的规律如图2所示．电子原来静止在左极板小孔处．下列说法中正确的是（　　）‎ A．从t=0时刻释放电子，电子将始终向右运动，直到打到右极板上 B．从t=0时刻释放电子，电子可能在两板间振动 C．从t=时刻释放电子，电子可能在两板间振动，也可能打到右极板上 D．从t=时刻释放电子，电子必将打到左极板上 ‎12．如图甲所示，A、B两块金属板水平放置，相距为d=0.6cm，两板间加有一周期性变化的电压，当B板接地（φB=0）时，A板电势φA，随时间变化的情况如图乙所示．现有一带负电的微粒在t=0时刻从B板中央小孔射入电场，若该带电徽粒受到的电场力为重力的两倍，且射入电场时初速度可忽略不计．求：‎ ‎（1）在0～和～T这两段时间内微粒的加速度大小和方向；‎ ‎（2）要使该微粒不与A板相碰，所加电压的周期最长为多少（g=10m/s2）．‎ ‎　‎ 五、动量与能量结合 ‎13．质量为M的小车置于水平面上．小车的上表面由圆弧和平面组成，车的右端固定有一不计质量的弹簧，圆弧AB部分光滑，半径为R，平面BC部分粗糙，长为l，C点右方的平面光滑．滑块质量为m，从圆弧最高处A无初速下滑（如图），与弹簧相接触并压缩弹簧，最后又返回到B相对于车静止．求：‎ ‎（1）BC部分的动摩擦因数μ；‎ ‎（2）弹簧具有的最大弹性势能；‎ ‎（3）当滑块与弹簧刚分离时滑块和小车的速度大小．‎ ‎14．如图所示，光滑水平面上放置质量均为M=2kg的甲．乙两辆小车，两车之间通过一感应开关相连（当滑块滑过感应开关时，两车自动分离）．其中甲车上表面光滑，乙车上表面与滑块P之间的动摩擦因数μ=0.5．一根通过细线拴着而被压缩的轻质弹簧固定在甲车的左端，质量为m=1kg的滑块P（可视为质点）与弹簧的右端接触但不相连，此时弹簧储存的弹性势能E0=10J，弹簧原长小于甲车长度，整个系统处于静止．现剪断细线，求：‎ ‎（i）滑块P刚滑上乙车时的速度大小；‎ ‎（ii）滑块P滑上乙车后最终未滑离乙车，P在乙车上滑行的距离为多大？‎ ‎15．如图所示是某游乐场过山车的娱乐装置原理图，弧形轨道末端与一个半径为R的光滑圆轨道平滑连接，两辆质量均为m的相同小车（大小可忽略），中间夹住一轻弹簧后连接在一起，两车从光滑弧形轨道上的某一高度由静止滑下，当两车刚滑入圆环最低点时连接两车的挂钩突然断开，弹簧将两车弹开，其中后车刚好停下，前车沿圆环轨道运动恰能越过圆弧轨道最高点，求：‎ ‎（1）前车被弹出时的速度；‎ ‎（2）前车被弹出的过程中弹簧释放的弹性势能；‎ ‎（3）两车从静止下滑到最低点的高度h．‎ ‎　‎ ‎2016-2017学年河南省新乡市高三（上）模拟物理试卷 参考答案与试题解析 ‎　‎ 一、有关摩擦力作用下的平衡问题 ‎1．如图所示，两个等大、反向的水平力F分别作用在物体A和B上，A、B两物体均处于静止状态．若各接触面与水平地面平行，则A、B两物体各受几个力？（　　）‎ A．3个、4个B．4个、4个C．4个、5个D．4个、6个 ‎【考点】力的合成与分解的运用；共点力平衡的条件及其应用．‎ ‎【分析】首先运用整体法得出地面与物体间没有摩擦力的作用，然后分别对AB进行受力分析即可得出物体受到几个力．‎ ‎【解答】解：对物体AB进行整体受力分析 水平方向：两个等大、反向的水平力F正好处于平衡，所以物体AB不受地面的摩擦力．‎ 对A物体进行受力分析：‎ 物体A在四个力的作用下处于平衡状态．故A受4个力．‎ 对物体B进行受力分析：‎ 物体B还受到物体A的弹力，所以物体B受5个力的作用．‎ 故选：C ‎　‎ ‎2．如图所示，倾角为θ的斜面体C置于水平面上，B置于斜面上，通过细绳跨过光滑的定滑轮与A相连，连接B的一段细绳与斜面平行，A、B、C都处于静止状态．则（　　）‎ A．B受到C的摩擦力一定不为零 B．C受到水平面的摩擦力一定为零 C．水平面对C的支持力与B、C的总重力大小相等 D．若将细绳剪断，B物体依然静止在斜面上，水平面对C的摩擦力为零 ‎【考点】共点力平衡的条件及其应用；静摩擦力和最大静摩擦力；力的合成与分解的运用．‎ ‎【分析】充分利用整体法和隔离体法对物体进行受力分析，结合摩擦力产生的条件，可判断各接触面是否存在摩擦力；把BC看做一个整体进行受力分析，可判定地面的支持力和二者重力的关系．‎ ‎【解答】解：A、当B受到绳子的拉力与B的重力在斜面上的分力大小相等，即mBgsinθ=mAg时，B在斜面上没有运动趋势，此时BC间没有摩擦力．选项A错误．‎ B、把BC当做一个整体进行受力分析，可知绳子的拉力在水平方向上的分量不为零，整体有向右的运动趋势，所以C受到地面的摩擦力不会为零．选项B错误．‎ C、把BC当做一个整体进行受力分析，在竖直方向上有：N+mAgsinθ=（mB+mC）g 绳子的拉力在竖直方向上的分量mAgsinθ不为零，所以水平面对C的支持力与B、C的总重力大小不相等．选项C错误．‎ D、若将细绳剪断，B物体依然静止在斜面上，以BC为整体进行受力分析，受重力和地面的支持力作用，在水平方向没有力作用，所以水平面对C的摩擦力为零．选项D正确．‎ 故选：D．‎ ‎　‎ ‎3．如图所示，一质量不计的弹簧原长为10cm，一端固定于质量m=2kg的物体上，另一端施一水平拉力F．（设最大静摩擦力与滑动摩擦力相等，g=10m/s2，弹簧始终在弹性限度内）‎ ‎（1）若物体与水平面间的动摩擦因数为0.2，当弹簧拉长至12cm时，物体恰好匀速运动，弹簧的劲度系数多大？‎ ‎（2）若将弹簧拉长至11cm，物体受到的摩擦力大小为多少？‎ ‎（3）若将弹簧拉长至13cm，物体受到的摩擦力大小为多少？‎ ‎【考点】共点力平衡的条件及其应用；滑动摩擦力；物体的弹性和弹力．‎ ‎【分析】（1）物体匀速运动时，弹簧的拉力与滑动摩擦力平衡，由平衡条件和胡克定律求出弹簧的劲度系数．‎ ‎（2）若将弹簧拉长到11cm时，弹簧的拉力小于最大静摩擦力，物体仍静止，由平衡条件求解物体所受到的静摩擦力大小．‎ ‎（2）若将弹簧拉长到13cm时，物体将加速前进，此时所受到的是滑动摩擦力，由平衡条件求解．‎ ‎【解答】解：（1）物体匀速运动时，根据平衡条件，有：‎ k（x﹣x0）=μmg 则：‎ k==N/m=200 N/m．‎ ‎（2）弹力：‎ F1=k（x1﹣x0）=200×（0.11﹣0.10）N=2 N 最大静摩擦力可看做等于滑动摩擦力，故：‎ Ffm=0.2×2×10 N=4 N 物体没动，故所受静摩擦力：‎ Ff1=F1=2 N．‎ ‎（3）弹力：‎ F2=k（x2﹣x0）=200×（0.13﹣0.10）N=6 N 物体将运动，此时所受到的滑动摩擦力为：‎ Ff2=μFN=μmg=0.2×2×10 N=4 N．‎ 答：（1）当弹簧长度为12cm时，物体恰好匀速运动，弹簧的劲度系数200N/m．‎ ‎（2）若将弹簧拉长到11cm时，物体所受到的摩擦力大小为2N．‎ ‎（3）若将弹簧拉长到13cm时，物体所受的摩擦力大小为4N．‎ ‎　‎ 二、万有引力与航天类问题 ‎4．美国国家科学基金会2010年9月29日宣布，天文学家发现一颗迄今为止与地球最类似的行星，该行星绕太阳系外的红矮星Gliese581做匀速圆周运动．这颗行星距离地球约20光年，公转周期约为37天，它的半径大约是地球的1.9倍，表面重力加速度与地球相近．下列说法正确的是（　　）‎ A．该行星的公转角速度比地球大 B．该行星的质量约为地球质量的3.61倍 C．该行星第一宇宙速度为7.9km/s D．要在地球上发射航天器到达该星球，发射速度只需达到地球的第二宇宙速度即可 ‎【考点】人造卫星的加速度、周期和轨道的关系；万有引力定律及其应用．‎ ‎【分析】根据万有引力提供向心力，得出轨道半径与周期的关系，得出地球的公转半径与该行星的公转半径关系，从而得出角速度的大小关系．根据万有引力等于重力，得出它们的质量关系．以及根据重力提供向心力求出第一宇宙速度的大小．‎ ‎【解答】解：A、根据，得，ω=，知地球的周期大于行星的周期，知地球的轨道半径大于行星的轨道半径，所以行星的角速度大于地球的角速度．故A正确．‎ B、根据，得M=，因为行星表面重力加速度与地球相近，半径大约是地球的1.9倍，则质量约为地球质量的3.61倍．故B正确．‎ C、根据mg=m，得v=，因为半径是地球的1.9倍，则第一宇宙速度是地球第一宇宙速度的倍．故C错误．‎ D、发射的速度达到地球的第二宇宙速度，将脱离地球的引力，绕太阳运行．故D错误．‎ 故选AB．‎ ‎　‎ ‎5．2011年7月，天文学家通过广域红外勘测器（WISE）发现地球首个特洛伊小行星．这颗小行星位于太阳﹣地球4号拉格朗日点．这颗小行星叫做2010TK7，直径接近300米，当前距离地球8 000万公里．它的公转轨道与地球相同，并始终在地球前方（打转），它陪伴着地球至少度过了几千年的时光．下面关于这颗小行星与地球的说法正确的是（　　）‎ A．绕太阳运动的向心加速度大小相等 B．受到太阳的万有引力大小相等 C．绕太阳运动的周期相等 D．在小行星运动一个周期过程中万有引力做正功 ‎【考点】万有引力定律及其应用．‎ ‎【分析】小行星绕太阳圆周运动的向心力由万有引力提供，根据小行星的轨道半径和地球的周期分析求解．‎ ‎【解答】解：A、小行星与地球围绕太阳公转，公转轨道与地球相同，根据，解得，其中M为太阳的质量，公转轨道半径相同，所以绕太阳运动的向心加速度大小相等，故A正确；‎ B、根据万有引力定律，小行星与地球质量不一定相等，所以受到太阳的万有引力大小不一定大小相等，故B错误；‎ C、小行星和地球均绕太阳公转，根据开普勒第三定律有，，知绕太阳运动运动的周期相等，故C正确；‎ D、小行星运动一个周期过程中，万有引力不做功，故D错误；‎ 故选：AC ‎　‎ ‎6．（多）气象卫星可以测量气象数据，分为两类．我国先后自行成功研制和发射了“风云Ⅰ号”和“风云Ⅱ号”两颗气象卫星，“风云Ⅰ号”卫星轨道与赤道平面垂直并且通过两极，称为“极地圆轨道”，每12h巡视地球一周．“风云Ⅱ号”气象卫星轨道平面在赤道平面内，称为“地球同步轨道”，每24h巡视地球一周，则“风云Ⅰ号”卫星比“风云Ⅱ号”卫星（　　）‎ A．线速度大B．发射速度小C．万有引力小D．向心加速度大 ‎【考点】人造卫星的加速度、周期和轨道的关系．‎ ‎【分析】风云Ⅱ号卫星为地球同步轨道卫星，周期为24h，卫星运行时万有引力提供向心力，可得线速度、万有引力和向心加速度与轨道半径的关系式，再进行分析．‎ ‎【解答】解：A、由卫星所受万有引力提供向心力，得：‎ F==m=ma v=，可知轨道半径越大，线速度越小，所以“风云Ⅰ号”卫星线速度大，故A正确；‎ B、由题意，“风云Ⅰ号”卫星比“风云Ⅱ号”卫星运行周期小，借助于开普勒定律可知，“风云Ⅰ号”卫星的轨道半径小，要向更高轨道发射卫星需要克服重力做更多的功，故高轨道卫星比低轨道的卫星需要更大的发射速度，所以可知“风云Ⅰ号”卫星发射速度小，故B正确．‎ C、万有引力F=，因为两卫星质量关系不清楚，不能判断万有引力的大小，故C错误．‎ D、加速度a=，可知“风云Ⅰ号”卫星向心加速度大，故D正确．‎ 故选：ABD ‎　‎ 三、传送带类问题 ‎7．如图所示，物体沿弧形轨道滑下后进入足够长的水平传送带，传送带以图示方向匀速运转，则传送带对物体做功情况可能是（　　）‎ A．始终不做功B．先做负功后做正功 C．先做正功后不做功D．先做负功后不做功 ‎【考点】功的计算．‎ ‎【分析】当物体到达传送带上时，物体的速度可能大于、等于和小于传送带的速度，分三种情况讨论即可得出结论．‎ ‎【解答】解：A、当物体到达传送带上时，如果物体的速度恰好和传送带的速度相等，那么物体和传送带将一起在水平面上运动，它们之间没有摩擦力的作用，所以传送带对物体始终不做功，所以A可能．‎ B、若物体速度大，则受向后的摩擦力，做负功．直至速度一致为止，摩擦力消失，不做功，不会出现再做正功的情况，所以B错误．‎ C、若物体速度小，则受向前的摩擦力，做正功．到速度一致时，摩擦力又变为零，不做功，所以C正确．‎ D、若物体速度大，则受向后的摩擦力，做负功．直至速度一致为止，摩擦力消失，不做功，所以D正确．‎ 故选：ACD ‎　‎ ‎8．在一水平向右匀速传输的传送带的左端A点，每隔T的时间，轻放上一个相同的工件，已知工件与传送带间动摩擦因素为μ，工件质量均为m，经测量，发现后面那些已经和传送带达到相同速度的工件之间的距离为x，下列判断正确的有（　　）‎ A．传送带的速度为 B．传送带的速度为2‎ C．每个工件与传送带间因摩擦而产生的热量为 D．在一段较长的时间t内，传送带因为传送工件而将多消耗的能量为 ‎【考点】牛顿第二定律；物理模型的特点及作用；功能关系．‎ ‎【分析】工件在传送带上先做匀加速直线运动，然后做匀速直线运动，每个工件滑上传送带后运动的规律相同，通过x=vT求出传送带的速度；根据工件和传送带之间的相对路程大小，求出摩擦产生的热量；根据能量守恒知，多消耗的能量一部分转化为工件的动能，一部分转化为摩擦产生的内能．‎ ‎【解答】解：A、工件在传送带上先做匀加速直线运动，然后做匀速直线运动，每个工件滑上传送带后运动的规律相同，可知x=vT，解得传送带的速度v=．故A正确．‎ B、设每个工件匀加速运动的位移为s，根据牛顿第二定律得，工件的加速度为μg，则传送带的速度，根据题目条件无法得出s与x的关系．故B错误．‎ C、工件与传送带相对滑动的路程为： =，‎ 则摩擦产生的热量为：Q=．故C错误．‎ D、根据能量守恒得，传送带因传送一个工件多消耗的能量E==，在时间t内，传送工件的个数n=，则多消耗的能量．故D正确．‎ 故选：AD．‎ ‎　‎ ‎9．一传送带装置示意图，其中传送带经过AB区域时是水平的，经过BC区域时变为圆弧形（圆弧由光滑模板形成，未画出），经过CD区域时是倾斜的，AB和CD都与BC相切．现将大量的质量均为m的小货箱一个一个在A处放到传送带上，放置时初速度为零，经传送带运送到D处，D和A的高度差为h．稳定工作时传送带速度不变，CD段上各箱等距排列，相邻两箱的距离为L．每个箱子在A处投放后，在到达B之前已经相对于传送带静止，且以后也不再滑动（忽略经BC段的微小滑动）．已知在一段相当长的时间T内，共运送小货箱的数目N个．这装置由电动机带动，传送带与轮子间无相对滑动，不计轮轴处的摩擦．求电动机的平均功率．‎ ‎【考点】功能关系；匀变速直线运动的公式；滑动摩擦力；功率、平均功率和瞬时功率．‎ ‎【分析】‎ 要求电动机的平均功率，需要知道在T时间内运送小货箱电动机所做的功，而电动机所做的功一是转化为小货箱的动能，二是转化为小货箱的重力势能，三是由于小货箱和传送带发生相对运动而产生的内能；由于每个小货箱都是从静止开始运动并且最后和传送带的速度相同，故每个小货箱获得的动能相同．又由于每个小货箱都是从底部运送到顶部，故每个小货箱增加的重力势能相同，同样产生的热量相同，故需要求出每个小货箱在加速的过程中产生的热量．而热量等于摩擦力与相对位移的乘积，故需要求解相对位移．‎ ‎【解答】解：以地面为参考系（下同），设传送带的运动速度为v0，在水平段运输的过程中，小货箱先在滑动摩擦力作用下做匀加速直线运动，其末速度等于传送带的速度，设这段时间内小货箱通过的位移为s，所用的时间为t，加速度为a，则对小货箱有 s=at2 ①‎ v0=at ②‎ 在这段时间内，传送带运动的路程为 s0=v0t ③‎ 由以上各式得 s0=2s ④‎ 用f表示小货箱与传送带之间的滑动摩擦力，则传送带对小货箱做功为 W1=fs=m ⑤‎ 传送带克服小箱对它的摩擦力做功 W0=fs0=2×m ⑥‎ 两者之差就是克服摩擦力做功发出的热量 Q=m ⑦‎ 可见，在小货箱加速运动过程中，小货箱获得的动能与系统因相对运动产生的热量相等．‎ T时间内，电动机输出的功为 W=T ⑧‎ 此功用于增加小货箱的动能、重力势能以及克服摩擦力产生热量，即 W=Nm+Nmgh+NQ ⑨‎ 已知相邻两小箱的距离为L，所以在T时间内运送的小货箱的个数N，‎ 则V0T=NL 　 ⑩‎ 联立⑦⑧⑨⑩式，得 ‎= [+gh]．‎ ‎　‎ 四、带电粒子在电场中的加速 ‎10．如图所示，A、B是一对中间有小孔的金属板，两小孔的连线与金属板面相垂直，两极板间的距离为L，两极板间加上低频交流电压，A板电势为零，B板电势为U=Uocosωt，现有一电子在t=0时刻从A板上的小孔进入电场，设初速度和重力的影响均可忽略不计，则电子在两极板间可能（　　）‎ A．以AB间的某一点为平衡位置来回振动 B．时而向B板运动，时而向A板运动，但最后穿出B板 C．一直向B板运动，最后穿出B板，如果ω小于某个值ωo，L小于某个值Lo D．一直向B板运动，最后穿出B板，而不论ω、L为何值 ‎【考点】带电粒子在匀强电场中的运动．‎ ‎【分析】两极板间加上低频交流电压，A板电势为零，B板电势为U=Uocosωt，B板电势周期性的变化，分过程研究，找出电场线的方向，‎ 根据牛顿第二定律确定电子受力方向和运动情况．‎ ‎【解答】解：A、如果两极板距离L足够大．‎ 在 0﹣，A板电势为零，B板电势为U=Uocosωt＞0，电场方向向左，使电子受力向右，电子向右加速运动，在时刻，电子速度最大，（T是交流电周期）‎ 在﹣，A板电势为零，B板电势为U=Uocosωt＜0，电场方向向右，使电子受力向左，电子向右减速运动，‎ 在﹣T，A板电势为零，B板电势为U=Uocosωt＜0，电场方向向右，使电子受力向左，电子开始向左做加速运动，在时刻，电子速度最大，‎ 在 T﹣T，A板电势为零，B板电势为U=Uocosωt＞0，电场方向向左，使电子受力向右，电子向左减速运动，在 T 时刻，电子速度减为0．‎ 以后重复上面所述的重复性运动，所以电子在两极AB间的某一点为平衡位置来回振动．故A正确，B错误 C、如果两极板距离L不是很大，那么电子可能在 0﹣内，一直加速运动并到达B板而穿出，‎ 也可能在﹣内，在正在减速时到达B板而穿出，故C正确，D错误． ‎ 故选：AC．‎ ‎　‎ ‎11．如图1所示，两平行金属板竖直放置，左极板接地，中间有小孔．右极板电势随时间变化的规律如图2所示．电子原来静止在左极板小孔处．下列说法中正确的是（　　）‎ A．从t=0时刻释放电子，电子将始终向右运动，直到打到右极板上 B．从t=0时刻释放电子，电子可能在两板间振动 C．从t=时刻释放电子，电子可能在两板间振动，也可能打到右极板上 D．从t=时刻释放电子，电子必将打到左极板上 ‎【考点】匀强电场中电势差和电场强度的关系．‎ ‎【分析】分析电子的受力情况，来分析电子的运动情况，若一直向右运动，可以打在右板，若电子时而向右运动，时而向左运动，根据位移关系，分析电子的运动情况 ‎【解答】解：分析电子在一个周期内的运动情况．‎ A、B从t=0时刻释放电子，前内，电子受到的电场力向右，电子向右做匀加速直线运动；后内，电子受到向左的电场力作用，电子向右做匀减速直线运动；接着周而复始，所以电子一直向右做单向的直线运动，直到打在右板上．故A正确，B错误．‎ C、从t=时刻释放电子，在﹣内，电子向右做匀加速直线运动；在﹣内，电子受到的电场力向左，电子继续向右做匀减速直线运动，时刻速度为零；在﹣T内电子受到向左的电场力，向左做初速度为零的匀加速直线运动，在T﹣内电子受到向右的电场力，向左做匀减速运动，在时刻速度减为零；接着重复．若两板距离足够大时，电子在两板间振动．故C正确．‎ D、用同样的方法分析从t=T时刻释放电子的运动情况，电子先向右运动，后向左运动，由于一个周期内向左运动的位移大于向右运动的位移，电子最终从左极板的小孔离开电场．也可能电子在向右过程中就碰到右极板，故D正确．‎ 故选：ACD ‎　‎ ‎12．如图甲所示，A、B两块金属板水平放置，相距为d=0.6cm，两板间加有一周期性变化的电压，当B板接地（φB=0）时，A板电势φA，随时间变化的情况如图乙所示．现有一带负电的微粒在t=0时刻从B板中央小孔射入电场，若该带电徽粒受到的电场力为重力的两倍，且射入电场时初速度可忽略不计．求：‎ ‎（1）在0～和～T这两段时间内微粒的加速度大小和方向；‎ ‎（2）要使该微粒不与A板相碰，所加电压的周期最长为多少（g=10m/s2）．‎ ‎【考点】带电粒子在匀强电场中的运动；牛顿第二定律．‎ ‎【分析】（1）根据牛顿第二定律求出加速度的大小和方向．‎ ‎（2）前半周期粒子向上匀加速运动，后半周期先向上做匀减速运动，后向下加速运动，根据牛顿第二定律和运动学公式求得微粒在一个周期内的总位移，再进行分析计算．‎ ‎【解答】解：（1）设电场力大小为F，则F=2mg，对于t=0时刻射入的微粒，在前半个周期内，有 ‎ F﹣mg=ma1‎ 又由题意，F=2mg 解得，a1=g，方向向上．‎ 后半个周期的加速度a2满足 ‎ F+mg=ma2‎ 得 a2=3g，方向向下．‎ ‎（2）前半周期上升的高度h1==‎ 前半周期微粒的末速度为v1=‎ 后半周期先向上做匀减速运动，设减速运动时间t1，则3gt1=，则得．‎ 此段时间内上升的高度 h2===‎ 则上升的总高度为H=h1+h2=‎ 后半周期的﹣t1=时间内，微粒向下加速运动，下降的高度H3==．‎ 上述计算表明，微粒在一个周期内的总位移为零，只要在上升过程中不与A板相碰即可，则H≤d，即≤d 所加电压的周期最长为Tm==6×10﹣2s 答：‎ ‎（1）在0～和～T这两段时间内微粒的加速度大小和方向分别为：g，方向向上和3g，方向向下；‎ ‎（2））要使该微粒不与A板相碰，所加电压的周期最长为6×10﹣2s．‎ ‎　‎ 五、动量与能量结合 ‎13．质量为M的小车置于水平面上．小车的上表面由圆弧和平面组成，车的右端固定有一不计质量的弹簧，圆弧AB部分光滑，半径为R，平面BC部分粗糙，长为l，C点右方的平面光滑．滑块质量为m，从圆弧最高处A无初速下滑（如图），与弹簧相接触并压缩弹簧，最后又返回到B相对于车静止．求：‎ ‎（1）BC部分的动摩擦因数μ；‎ ‎（2）弹簧具有的最大弹性势能；‎ ‎（3）当滑块与弹簧刚分离时滑块和小车的速度大小．‎ ‎【考点】动量守恒定律；牛顿第二定律；功能关系．‎ ‎【分析】（1）滑块与小车初始状态为静止，末状态滑块相对小车静止，即两者共速且速度为0，据能量守恒求解 ‎（2）弹簧压缩到最大形变量时，滑块与小车又一次共速，且速度均为0，据能量守恒求解．‎ ‎（3）弹簧与滑块分离的时候，弹簧的弹性能为0，据能量守恒和系统动量守恒求解．‎ ‎【解答】解：（1）滑块与小车初始状态为静止，末状态滑块相对小车静止，即两者共速且速度为0，‎ 据能量守恒：‎ mgR=μmg•2l，‎ ‎∴‎ ‎（2）弹簧压缩到最大形变量时，滑块与小车又一次共速，且速度均为0，此时据能量守恒，‎ 弹簧的弹性势能 ‎（3）弹簧与滑块分离的时候，弹簧的弹性能为0，设此时滑块速度为v1，小车速度为v2据能量守恒有：‎ ‎ 又因为系统动量守恒，有：mv1﹣Mv2=0‎ 解得：‎ 答：（1）BC部分的动摩擦因数；‎ ‎（2）弹簧具有的最大弹性势能是；‎ ‎（3）当滑块与弹簧刚分离时滑块和小车的速度大小分别是，．‎ ‎　‎ ‎14．如图所示，光滑水平面上放置质量均为M=2kg的甲．乙两辆小车，两车之间通过一感应开关相连（当滑块滑过感应开关时，两车自动分离）．其中甲车上表面光滑，乙车上表面与滑块P之间的动摩擦因数μ=0.5．一根通过细线拴着而被压缩的轻质弹簧固定在甲车的左端，质量为m=1kg的滑块P（可视为质点）与弹簧的右端接触但不相连，此时弹簧储存的弹性势能E0=10J，弹簧原长小于甲车长度，整个系统处于静止．现剪断细线，求：‎ ‎（i）滑块P刚滑上乙车时的速度大小；‎ ‎（ii）滑块P滑上乙车后最终未滑离乙车，P在乙车上滑行的距离为多大？‎ ‎【考点】动量守恒定律；机械能守恒定律．‎ ‎【分析】（i）由动量守恒定律与能量守恒定律可以求出滑块的速度；‎ ‎（ii）以滑块与小车乙组成的系统为研究对象，应用动量守恒定律与能量守恒定律可以小车的长度．‎ ‎【解答】解：（i）设滑块P刚滑上乙车时的速度为v1，此时两车的速度为v2，‎ 以两车与滑块组成的系统为研究对象，以向右为正方向，‎ 由动量守恒定律得：mv1﹣2Mv2=0，‎ 由能量守恒定律得：E0=，‎ 解得：v1=4m/s；‎ ‎（ii）设滑块P和小车乙达到的共同速度为v，滑块P在乙车上滑行的距离为L，‎ 以滑块P和小车乙组成的系统为研究对象，以向右为正方向，‎ 由动量守恒守恒定律得：mv1﹣Mv2=（m+M）v，‎ 由能量守恒定律得：μmgL=+﹣，‎ 解得：L=m；‎ 答：（i）滑块P刚滑上乙车时的速度大小为4m/s；‎ ‎（ii）滑块P滑上乙车后最终未滑离乙车，P在乙车上滑行的距离为多m．‎ ‎　‎ ‎15．如图所示是某游乐场过山车的娱乐装置原理图，弧形轨道末端与一个半径为R的光滑圆轨道平滑连接，两辆质量均为m的相同小车（大小可忽略），中间夹住一轻弹簧后连接在一起，两车从光滑弧形轨道上的某一高度由静止滑下，当两车刚滑入圆环最低点时连接两车的挂钩突然断开，弹簧将两车弹开，其中后车刚好停下，前车沿圆环轨道运动恰能越过圆弧轨道最高点，求：‎ ‎（1）前车被弹出时的速度；‎ ‎（2）前车被弹出的过程中弹簧释放的弹性势能；‎ ‎（3）两车从静止下滑到最低点的高度h．‎ ‎【考点】动量守恒定律；机械能守恒定律．‎ ‎【分析】（1）前车沿圆环轨道运动恰能越过圆弧轨道最高点，根据牛顿第二定律求出最高点速度，根据机械能守恒列出等式求解 ‎（2）由动量守恒定律求出两车分离前速度，根据系统机械能守恒求解 ‎（3）两车从h高处运动到最低处机械能守恒列出等式求解．‎ ‎【解答】解：（1）设前车在最高点速度为v2，依题意有（1）‎ 设前车在最低位置与后车分离后速度为v1，根据机械能守恒得 ‎（2）‎ 由（1）（2）得：v1=‎ ‎（2）设两车分离前速度为v0，‎ 由动量守恒定律2mv0=mv1‎ 得 设分离前弹簧弹性势能Ep，根据系统机械能守恒得 ‎（3）两车从h高处运动到最低处机械能守恒 答：（1）前车被弹出时的速度是；‎ ‎（2）前车被弹出的过程中弹簧释放的弹性势能是；‎ ‎（3）两车从静止下滑到最低点的高度是．‎ ‎　‎ ‎2016年12月2日