陕西省西安八十三中2016届高三上学期第一次段考物理试卷 28页

‎2015-2016学年陕西省西安八十三中高三（上）第一次段考物理试卷 ‎　‎ 一、选择题：本题共16小题，每小题3分，共48分．在每小题给出的四个选项中，第1～9题只有一项符合题目要求，第10～16题有多选符合题目要求．全部选对的得3分，选对但不全的得2分，有选错的得0分．‎ ‎1．下列说法中正确的是（　　）‎ A．“北京时间10点整”和“一节课40min”指的都是时间 B．在某次铅球比赛中，某运动员以18.62米的成绩获得金牌，这里记录的成绩是比赛中铅球经过的路程 C．瞬时速度可理解为时间趋于零时的平均速度 D．物体运动的加速度越来越大，则速度一定也越来越大 ‎2．如图所示，甲、乙、丙、丁分别代表四辆车由同一地点同时开始沿同一方向运动的位移﹣﹣时间图象和速度﹣﹣时间图象，则下列说法正确的是（　　）‎ A．甲车做曲线运动，乙车做直线运动 B．0～t1时间内，甲车的平均速度大于乙车的平均速度 C．在t2时刻丁车在丙车的前面 D．0～t2时间内，丙车做匀变速直线运动，丁车做加速度增加的加速运动 ‎3．一辆汽车以10m/s的速度沿平直公路匀速运动，司机发现前方有障碍物立即减速，以0.2m/s2的加速度做匀减速运动，减速后一分钟内汽车的位移为（　　）‎ A．240m B．250m C．260m D．90m ‎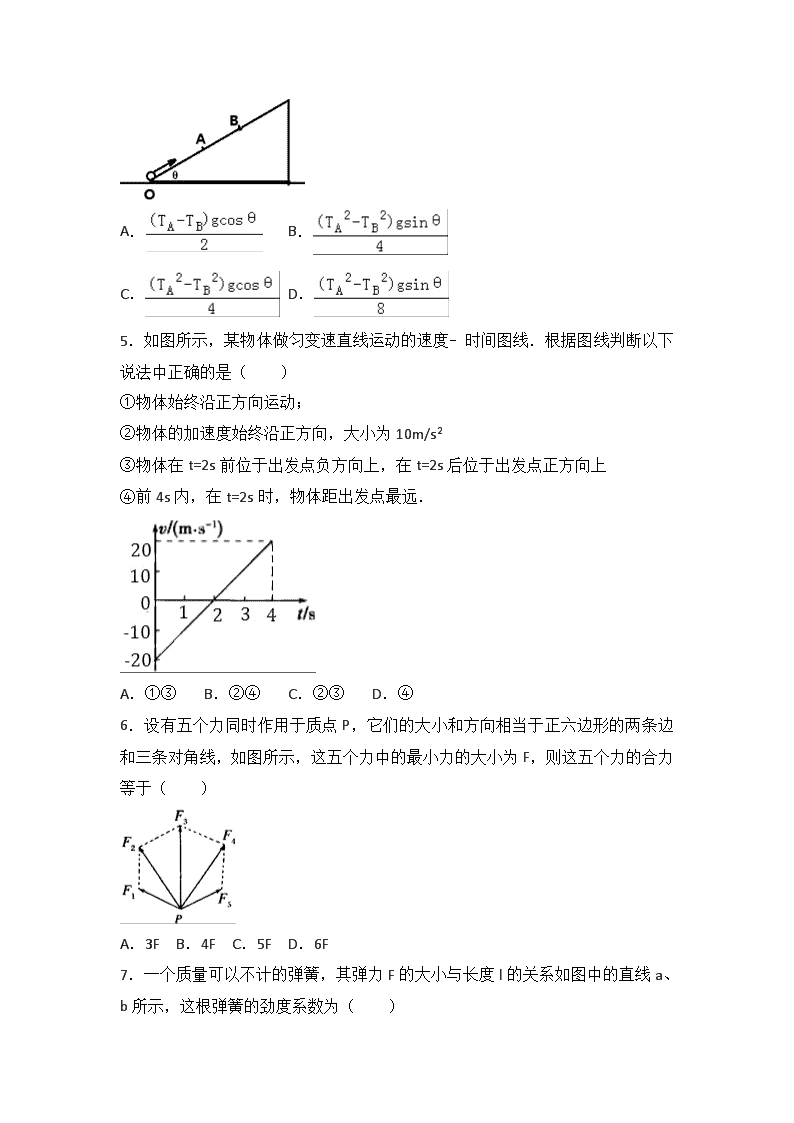4．如图所示，一个小球从倾角为θ的光滑斜面底端O以一定速度冲上斜面．已知小球两次经过一个较低点A的时间间隔为TA，两次经过较高点B的时间间隔为TB，重力加速度为g，则A、B两点间的距离为（　　）‎ A． B．‎ C． D．‎ ‎5．如图所示，某物体做匀变速直线运动的速度﹣时间图线．根据图线判断以下说法中正确的是（　　）‎ ‎①物体始终沿正方向运动； ‎ ‎②物体的加速度始终沿正方向，大小为10m/s2‎ ‎③物体在t=2s前位于出发点负方向上，在t=2s后位于出发点正方向上 ‎④前4s内，在t=2s时，物体距出发点最远．‎ A．①③ B．②④ C．②③ D．④‎ ‎6．设有五个力同时作用于质点P，它们的大小和方向相当于正六边形的两条边和三条对角线，如图所示，这五个力中的最小力的大小为F，则这五个力的合力等于（　　）‎ A．3F B．4F C．5F D．6F ‎7．一个质量可以不计的弹簧，其弹力F的大小与长度l的关系如图中的直线a、b所示，这根弹簧的劲度系数为（　　）‎ A．1250N/m B．625N/m C．2500N/m D．833N/m ‎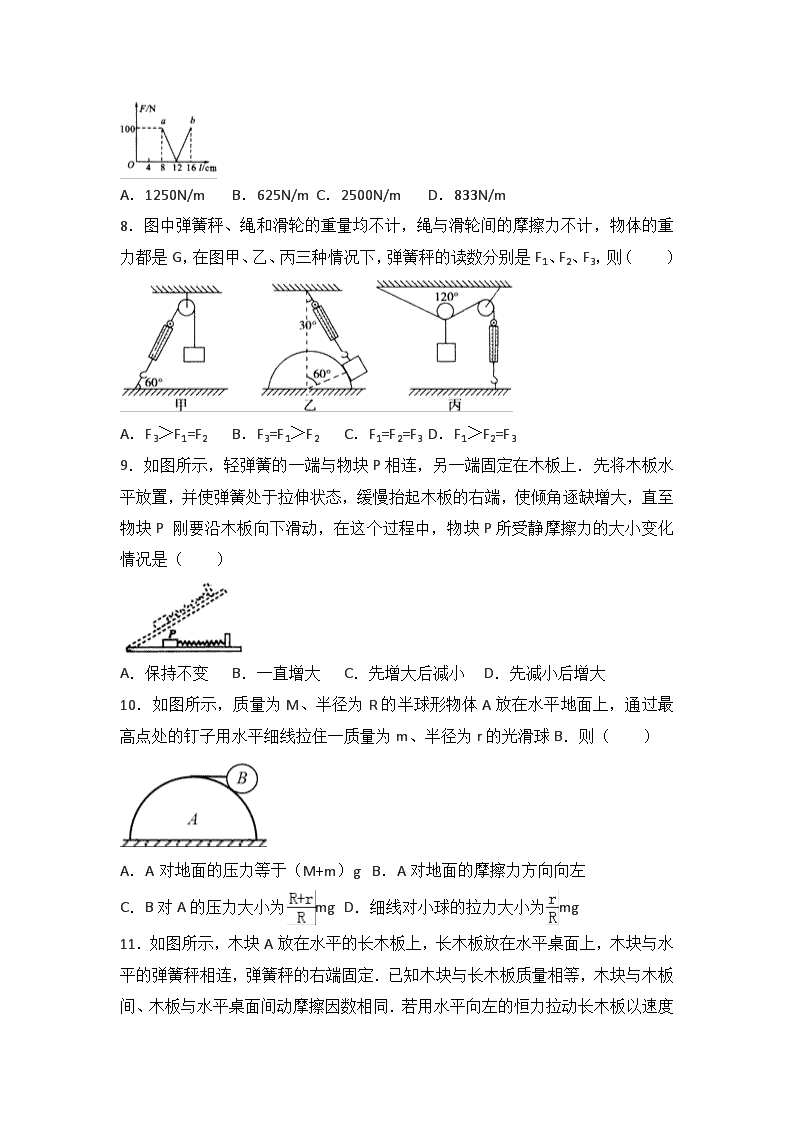8．图中弹簧秤、绳和滑轮的重量均不计，绳与滑轮间的摩擦力不计，物体的重力都是G，在图甲、乙、丙三种情况下，弹簧秤的读数分别是F1、F2、F3，则（　　）‎ A．F3＞F1=F2 B．F3=F1＞F2 C．F1=F2=F3 D．F1＞F2=F3‎ ‎9．如图所示，轻弹簧的一端与物块P相连，另一端固定在木板上．先将木板水平放置，并使弹簧处于拉伸状态，缓慢抬起木板的右端，使倾角逐缺增大，直至物块P 刚要沿木板向下滑动，在这个过程中，物块P所受静摩擦力的大小变化情况是（　　）‎ A．保持不变 B．一直增大 C．先增大后减小 D．先减小后增大 ‎10．如图所示，质量为M、半径为R的半球形物体A放在水平地面上，通过最高点处的钉子用水平细线拉住一质量为m、半径为r的光滑球B．则（　　）‎ A．A对地面的压力等于（M+m）g B．A对地面的摩擦力方向向左 C．B对A的压力大小为mg D．细线对小球的拉力大小为mg ‎11．如图所示，木块A放在水平的长木板上，长木板放在水平桌面上，木块与水平的弹簧秤相连，弹簧秤的右端固定．已知木块与长木板质量相等，木块与木板间、木板与水平桌面间动摩擦因数相同．若用水平向左的恒力拉动长木板以速度v匀速运动时，弹簧秤的示数为FT，则（　　）‎ A．木块A受到的静摩擦力等于FT B．木块A受到的滑动摩擦力等于FT C．若用恒力以2v的速度匀速向左拉动长木板，弹簧秤的示数为2FT D．若用恒力以2v的速度匀速向左拉动长木板，该恒力大小为3FT ‎12．如图甲所示，在粗糙水平面上静置一个截面为等腰三角形的斜劈A，其质量为M，两个底角均为30°．两个完全相同的、质量均为m的小物块p和q恰好能沿两侧匀速下滑．若现在对两物块同时各施加一平行于斜劈侧面的力F1、F2，且F1＜F2，如图乙所示，则在p和q下滑的过程中，下列说法正确的是（　　）‎ A．斜劈A仍保持静止 B．斜劈A受到地面向右的摩擦力作用 C．斜劈A对地面的压力小于（M+2m）g D．斜劈A对地面的压力大于（M+2m）g ‎13．如图所示，将两个质量均为m的小球a、b用细线相连悬挂于O点，两绳可承受的最大张力为3.5mg．先用力F拉住小球a，使整个装置处于平衡状态，并保持悬线Oa与竖直方向的夹角为θ=30°不变，则F的大小可能为（　　）‎ A． mg B．mg C． mg D．3mg ‎14．在平直公路上，汽车以10m/s的速度匀速驶向路口，当行驶至距路口停车线20m处时，还有3s绿灯就要熄灭．而该汽车在绿灯熄灭时刚好停在停车线处，则汽车运动的速度﹣时间图象可能是图中的（　　）‎ A． B． C． D．‎ ‎15．一物体做匀加速直线运动，在 2s 内通过的位移为 6m，在紧接着的 1s 内通过的位移也为 6m．则物体运动的初速度v0和加速度a的大小（　　）‎ A．v0=1m/s B．v0=2m/s C．a=1m/s2 D．a=2m/s2‎ ‎16．某司机在检测汽车性能过程中，得到汽车减速过程中的位移s与速度v的关系曲线如图所示，并得出位移s与速度v的函数关系式为s=m﹣nv2，其中m、n为常数．重力加速度的大小g取10m/s2．则以下判断正确的是（　　）‎ A．汽车在此过程中做匀变速直线运动 B．汽车的末速度为20m/s C．由题中所给已知条件可确定m、n的大小 D．汽车对司机作用力的大小与司机重力大小的比值为 ‎　‎ 二、实验题：本题共2小题，共12分 ‎17．如图所示是某同学在做匀变速直线运动实验中获得的一条纸带，打点计时器电源频率为50Hz，A、B、C、D是纸带上四个计数点，每两个相邻计数点间有四个点没有画出．从图中读出A、B两点间距x=　　cm；B点对应的速度是　　m/s；物体运动的加速度是　　m/s2．（计算结果保留二位有效数字）．‎ ‎18．橡皮筋也像弹簧一样，在弹性限度内，伸长量x与弹力F成正比，即F=kx，k的值与橡皮筋未受到拉力时的长度L、横截面积S有关，理论与实践都表明k=Y ‎，其中Y是一个由材料决定的常数，材料力学上称之为杨氏模量．‎ ‎（1）在国际单位制中，杨氏模量Y的单位应该是　　‎ A．N B．m C．N/m D．Pa ‎（2）有一段横截面是圆形的橡皮筋，应用如图所示的实验装置可以测量出它的杨氏模量Y的值．首先利用测量工具a测得橡皮筋的长度L=20.00cm，利用测量工具b测得橡皮筋未受到拉力时的直径D=4.000mm，那么测量工具a应该是　　，测量工具b应该是　　．‎ ‎（3）下面的表格是橡皮筋受到的拉力F与伸长量x的实验记录．‎ 拉力F/N ‎5‎ ‎10‎ ‎15‎ ‎20‎ ‎25‎ 伸长量x/cm ‎1.6‎ ‎3.2‎ ‎4.7‎ ‎6.4‎ ‎8.0‎ 可求得该橡皮筋的劲度系数k=　　N/m．‎ ‎（4）这种橡皮筋的Y值等于　　．‎ ‎　‎ 三、计算题：本题共4小题，共40分．要求写出必要的文字说明、主要方程式和重要演算步骤，有数值计算的要明确写出数值和单位，只有最终结果的不得分．‎ ‎19．如图所示，用一根轻质、光滑且不可伸长的绳子晾晒衣服，绳长L，绳子的两端分别固定在间距为d的两根竖直杆上（已知L＞d），衣服及衣服撑的总质量为m，重力加速度为g，当利用衣服撑把衣服挂到此绳子上静止后，求此时绳子的张力大小．‎ ‎20．如图所示，质量为m的物体，放在一固定斜面上，当斜面倾角为θ=30°时恰能沿斜面匀速下滑．重力加速度为g．‎ ‎（1）物体与斜面间的动摩擦因数μ；‎ ‎（2）现对物体施加一大小为F的水平向右恒力，使物体可沿斜面匀速向上滑行．求F的大小（用m、g、θ表示）．（要求画出受力分析图）‎ ‎（3）设最大静摩擦力等于滑动摩擦力，当斜面倾角增大并超过某一临界角θ0时，不论水平恒力F多大，都不能使物体沿斜面向上滑行．求这一临界角θ0的大小．‎ ‎21．据英国《每日邮报》报道，英国触式橄榄球球员赫普顿斯托尔在伦敦成功挑战地铁速度．他从“市长官邸站”下车，在下一地铁站“坎农街站”在车门快关上前成功跑回同一节车厢．‎ 已知西安地铁一号线某两站间距离约为x=600m，地铁列车每次停站时间（从车门打开到关闭的时间）为ta=45s，列车加速和减速的加速度大小均为a=1m/s2，运行过程的最大速度为vm=54km/h．假设列车运行过程中只做匀变速和匀速运动，两站之间的地铁轨道和地面道路都是平直的且长度相同，出站和进站最短共需用时tb=70s． 若有人想在这两个地铁车站间挑战地铁速度，他在地面道路上奔跑的平均速度至少多大？‎ ‎22．甲、乙两车在平直公路上比赛，某一时刻，乙车在甲车前方L1=11m处，乙车速度v乙=60m/s，甲车速度v甲=50m/s，此时乙车离终点线尚有L2=600m，如图所示．若甲车做匀加速运动，加速度a=2m/s2，乙车速度不变，不计车长．‎ ‎（1）经过多长时间甲、乙两车间距离最大，最大距离是多少？‎ ‎（2）到达终点时甲车能否超过乙车？‎ ‎　‎ ‎2015-2016学年陕西省西安八十三中高三（上）第一次段考物理试卷 参考答案与试题解析 ‎　‎ 一、选择题：本题共16小题，每小题3分，共48分．在每小题给出的四个选项中，第1～9题只有一项符合题目要求，第10～16题有多选符合题目要求．全部选对的得3分，选对但不全的得2分，有选错的得0分．‎ ‎1．下列说法中正确的是（　　）‎ A．“北京时间10点整”和“一节课40min”指的都是时间 B．在某次铅球比赛中，某运动员以18.62米的成绩获得金牌，这里记录的成绩是比赛中铅球经过的路程 C．瞬时速度可理解为时间趋于零时的平均速度 D．物体运动的加速度越来越大，则速度一定也越来越大 ‎【考点】时间与时刻；位移与路程；加速度．‎ ‎【分析】路程是物体运动轨迹的长度，位移是从初位置到末位置的有向线段，当时间趋向于零时，平均速度等于瞬时速度，时间是指时间的长度，在时间轴上对应时间段，时刻是指时间点，在时间轴上对应的是一个点．‎ ‎【解答】解：A、北京时间10点整在时间轴上对应的是一个点，所以是时刻，一节课40min在时间轴上对应的是一个线段，表示时间，故A错误；‎ B、铅球比赛中，铅球的运动轨迹是曲线，成绩是测量初末位置的水平方向距离，所以记录的成绩是比赛中铅球的水平位移，故B错误；‎ C、根据可知，当时间趋向于零时，平均速度等于瞬时速度，故C正确；‎ D、当加速度与速度方向相反时，加速度增大，速度越来越小，故D错误．‎ 故选：C ‎　‎ ‎2．如图所示，甲、乙、丙、丁分别代表四辆车由同一地点同时开始沿同一方向运动的位移﹣﹣时间图象和速度﹣﹣时间图象，则下列说法正确的是（　　）‎ A．甲车做曲线运动，乙车做直线运动 B．0～t1时间内，甲车的平均速度大于乙车的平均速度 C．在t2时刻丁车在丙车的前面 D．0～t2时间内，丙车做匀变速直线运动，丁车做加速度增加的加速运动 ‎【考点】匀变速直线运动的图像；匀变速直线运动的速度与时间的关系．‎ ‎【分析】在位移﹣时间图象中，倾斜的直线表示物体做匀速直线运动，图线切线的斜率表示速度，图象的交点表示位移相等，平均速度等于位移除以时间；‎ 在速度﹣时间图象中，倾斜的直线表示物体做匀变速直线运动，图线的斜率表示加速度，图象与时间轴围成的面积表示位移．‎ ‎【解答】解：‎ A、由位移时间图线切线的斜率表示速度，由图象可知：乙做匀速直线运动，甲做减速直线运动，故A错误；‎ B、在t1时刻两车的位移相等，又都是单向直线运动，所用时间相等，所以两车平均速度相等，故B错误；‎ C、由速度图象与时间轴围成的面积表示位移可知：在t2时刻丁的位移大于丙的位移，而两车又是从同一地点向同一方向做直线运动，所以在t2时刻丁车在丙车的前面，故C正确；‎ D、0～t2时间内，丙车都做匀变速直线运动，丁车做加速度减小的变加速直线运动，故D错误．‎ 故选：C ‎　‎ ‎3．一辆汽车以10m/s的速度沿平直公路匀速运动，司机发现前方有障碍物立即减速，以0.2m/s2的加速度做匀减速运动，减速后一分钟内汽车的位移为（　　）‎ A．240m B．250m C．260m D．90m ‎【考点】匀变速直线运动的位移与时间的关系．‎ ‎【分析】根据匀变速直线运动的速度时间公式求出汽车速度减为零的时间，判断汽车是否停止，再结合位移公式求出减速后一分钟内汽车的位移．‎ ‎【解答】解：汽车速度减为零的时间t=，‎ 则减速1分钟内的位移等于50s内的位移，即x=．故B正确，A、C、D错误．‎ 故选：B．‎ ‎　‎ ‎4．如图所示，一个小球从倾角为θ的光滑斜面底端O以一定速度冲上斜面．已知小球两次经过一个较低点A的时间间隔为TA，两次经过较高点B的时间间隔为TB，重力加速度为g，则A、B两点间的距离为（　　）‎ A． B．‎ C． D．‎ ‎【考点】匀变速直线运动规律的综合运用．‎ ‎【分析】根据牛顿第二定律求出小球在斜面上的加速度大小，根据小球上滑和下滑的对称性得出从最高点到A点的时间和最高点到B的时间，结合位移时间公式求出A、B两点间的距离．‎ ‎【解答】解：根据牛顿第二定律得，小球的加速度a=，‎ 小球两次经过一个较低点A的时间间隔为TA，根据对称性知，在最高点返回到A点的时间，在最高点返回到B点的时间，‎ 则A、B两点间的距离==‎ ‎．‎ 故选：D．‎ ‎　‎ ‎5．如图所示，某物体做匀变速直线运动的速度﹣时间图线．根据图线判断以下说法中正确的是（　　）‎ ‎①物体始终沿正方向运动； ‎ ‎②物体的加速度始终沿正方向，大小为10m/s2‎ ‎③物体在t=2s前位于出发点负方向上，在t=2s后位于出发点正方向上 ‎④前4s内，在t=2s时，物体距出发点最远．‎ A．①③ B．②④ C．②③ D．④‎ ‎【考点】匀变速直线运动的图像；匀变速直线运动的速度与时间的关系．‎ ‎【分析】物体在前2s内沿负方向运动，后2s内沿正方向运动，速度方向相反．速度图象的斜率表示加速度，t=2s前与t=2s后相比，直线的斜率相同，加速度相同．在t=4s时，物体离出发点的位移最小，为零．‎ ‎【解答】解：①速度的正负表示物体的运动方向，则知物体在前2s内沿负方向运动，后2s内沿正方向运动．故①错误．‎ ‎②根据图象的斜率表示加速度，可知物体的加速度始终沿正方向，大小为 a===10m/s2．故②正确．‎ ‎③、④t=0时物体位于原点，前2s物体沿负方向运动，t=2s时离出发点最远，后沿正方向运动，t=4s时回到出发点，故0﹣4s内物体一直位于出发点负方向，故③错误 ④正确．‎ 故选：B ‎　‎ ‎6．设有五个力同时作用于质点P，它们的大小和方向相当于正六边形的两条边和三条对角线，如图所示，这五个力中的最小力的大小为F，则这五个力的合力等于（　　）‎ A．3F B．4F C．5F D．6F ‎【考点】力的合成．‎ ‎【分析】多个力合成时可以先合成任意两个力，再把这两个力的合力与第三个力相合成，只到把所有的力都合成进去，即可求得最后的合力．‎ ‎【解答】解：如图所示，F1与F4的合力与F3同向；同时F2与F5的合力也与F3同向；故分别将F1与F5合成，F2与F4合成，两个合力与F3在同一直线上；根据平行四边形定则，F1和F4的合力为F3，F2和F5的合力为F3，所以五个力的合力等于3F3，因为F1=F，根据几何关系知，F3=2F，所以五个力的合力大小为6F，方向沿F3方向．‎ 故选D．‎ ‎　‎ ‎7．一个质量可以不计的弹簧，其弹力F的大小与长度l的关系如图中的直线a、b所示，这根弹簧的劲度系数为（　　）‎ A．1250N/m B．625N/m C．2500N/m D．833N/m ‎【考点】胡克定律．‎ ‎【分析】‎ 由图中的弹力为零可得到弹簧的原长，进而由a或b的对应坐标可得劲度系数．‎ ‎【解答】解：由图知当l=12cm时，F=0，故弹黄原长l0=12cm．‎ 而由图知l=16cm，知弹簧形变量为△x=l﹣l0=4cm时，此时F=100N，由胡克定律可得：‎ 故C正确．‎ 故选：C．‎ ‎　‎ ‎8．图中弹簧秤、绳和滑轮的重量均不计，绳与滑轮间的摩擦力不计，物体的重力都是G，在图甲、乙、丙三种情况下，弹簧秤的读数分别是F1、F2、F3，则（　　）‎ A．F3＞F1=F2 B．F3=F1＞F2 C．F1=F2=F3 D．F1＞F2=F3‎ ‎【考点】共点力平衡的条件及其应用；力的合成与分解的运用．‎ ‎【分析】弹簧称的读数等于弹簧受到的拉力．甲图、乙图分别以物体为研究对象由平衡条件求解．丙图以动滑轮为研究对象分析受力情况，根据平衡条件求解．‎ ‎【解答】解：甲图：物体静止，弹簧的拉力F1=mg；‎ ‎ 乙图：对物体为研究对象，作出力图如图．‎ 由平衡条件得 ‎ F2=Gsin60°==0.866mg 丙图：以动滑轮为研究对象，受力如图．由几何知识得F3=mg．故F3=F1＞F2‎ 故选B ‎　‎ ‎9．如图所示，轻弹簧的一端与物块P相连，另一端固定在木板上．先将木板水平放置，并使弹簧处于拉伸状态，缓慢抬起木板的右端，使倾角逐缺增大，直至物块P 刚要沿木板向下滑动，在这个过程中，物块P所受静摩擦力的大小变化情况是（　　）‎ A．保持不变 B．一直增大 C．先增大后减小 D．先减小后增大 ‎【考点】共点力平衡的条件及其应用；力的合成与分解的运用；胡克定律．‎ ‎【分析】由题，缓慢抬起木板的右端，使倾角逐渐增大的过程中，物块P的重力沿木板向下的分力先小于弹簧的弹力，后大于弹簧的弹力，根据平衡条件分析物块P所受静摩擦力的大小变化情况．‎ ‎【解答】解：设物块的重力为G，木板与水平面的夹角为θ，弹簧的弹力大小为F，静摩擦力大小为f．‎ 由题，缓慢抬起木板的右端，使倾角逐渐增大，直至物块P刚要沿木板向下滑动的过程中，弹簧的拉力不变，物块P的重力沿木板向下的分力先小于弹簧的弹力，后大于弹簧的弹力，物块P所受的静摩擦力方向先木板向下，后沿木板向上．‎ 当物块P的重力沿木板向下的分力小于弹簧的弹力时，则有Gsinθ+f=F，θ增大时，F不变，f减小；‎ 当物块P的重力沿木板向下的分力大于等于弹簧的弹力时，则有Gsinθ=f+F，θ增大时，F不变，f增大；‎ 所以物块P所受静摩擦力的大小先减小后增大．‎ 故选：D．‎ ‎　‎ ‎10．如图所示，质量为M、半径为R的半球形物体A放在水平地面上，通过最高点处的钉子用水平细线拉住一质量为m、半径为r的光滑球B．则（　　）‎ A．A对地面的压力等于（M+m）g B．A对地面的摩擦力方向向左 C．B对A的压力大小为mg D．细线对小球的拉力大小为mg ‎【考点】共点力平衡的条件及其应用；力的合成与分解的运用．‎ ‎【分析】先对整体受力分析，然后根据共点力平衡条件分析AB选项，再隔离B物体受力分析后根据平衡条件分析CD选项．‎ ‎【解答】解：AB、对AB整体受力分析，受重力和支持力，相对地面无相对滑动趋势，故不受摩擦力，根据平衡条件，支持力等于整体的重力，为（M+m）g；根据牛顿第三定律，整体对地面的压力与地面对整体的支持力是相互作用力，大小相等，故对地面的压力等于（M+m）g，故A正确，B错误；‎ CD、对小球受力分析，如图所示：‎ 根据平衡条件，有：F=，T=mgtanθ 其中cosθ=，tanθ=，‎ 故：F=，T=mg 故C正确，D错误；‎ 故选：AC．‎ ‎　‎ ‎11．如图所示，木块A放在水平的长木板上，长木板放在水平桌面上，木块与水平的弹簧秤相连，弹簧秤的右端固定．已知木块与长木板质量相等，木块与木板间、木板与水平桌面间动摩擦因数相同．若用水平向左的恒力拉动长木板以速度v匀速运动时，弹簧秤的示数为FT，则（　　）‎ A．木块A受到的静摩擦力等于FT B．木块A受到的滑动摩擦力等于FT C．若用恒力以2v的速度匀速向左拉动长木板，弹簧秤的示数为2FT D．若用恒力以2v的速度匀速向左拉动长木板，该恒力大小为3FT ‎【考点】物体的弹性和弹力；摩擦力的判断与计算．‎ ‎【分析】当长木板B匀速运动时，A保持静止．以A为研究对象，根据平衡条件研究B对A的滑动摩擦力的大小．根据滑动摩擦力公式f=μFN，可知滑动摩擦力大小与动摩擦因数和压力成正比，与物体的速度大小无关．‎ ‎【解答】解：A、稳定时，A保持静止．A水平方向受到弹簧的拉力和B对A的滑动摩擦力，由平衡条件得到，木块A受到的滑动摩擦力的大小等于弹簧的拉力FT．故A错误，B正确；‎ C、若长木板B以2v的速度匀速运动时，AB间动摩擦因数不变，A对B的压力不变，则木块A受到的滑动摩擦力的大小不变，仍等于FT，则弹簧秤的示数为FT，故C错误；‎ D、木板做匀速运动，受力平衡，对木板受力分析，水平方向受到拉力F，A对木板向右的滑动摩擦力FT以及地面对木板向右的滑动摩擦力f，因为木块与长木板质量相等，动摩擦因数相同，则f=2FT，‎ 根据平衡条件得：F=3FT，故D正确．‎ 故选：BD ‎　‎ ‎12．如图甲所示，在粗糙水平面上静置一个截面为等腰三角形的斜劈A，其质量为M，两个底角均为30°．两个完全相同的、质量均为m的小物块p和q恰好能沿两侧匀速下滑．若现在对两物块同时各施加一平行于斜劈侧面的力F1、F2，且F1＜F2，如图乙所示，则在p和q下滑的过程中，下列说法正确的是（　　）‎ A．斜劈A仍保持静止 B．斜劈A受到地面向右的摩擦力作用 C．斜劈A对地面的压力小于（M+2m）g D．斜劈A对地面的压力大于（M+2m）g ‎【考点】摩擦力的判断与计算；物体的弹性和弹力．‎ ‎【分析】甲图中，三个物体都处于平衡状态，故可以对三个物体的整体受力分析，根据平衡条件判断整体与地面间的弹力和摩擦力情况；在图乙中，物体P、q对斜劈的压力和摩擦力不变，故斜劈受力情况不变 ‎【解答】解：甲图中，三个物体都处于平衡状态，故可以对三个物体的整体受力分析，受重力和支持力，故支持力为（M+2m）g，没有摩擦力；‎ 在图乙中，物体P、q对斜劈的压力和摩擦力大小不变，故斜劈受力情况不变，故斜劈A仍保持静止，斜劈A对地面的压力大小等于（M+2m）g，与地面间没有摩擦力；‎ 故选：A ‎　‎ ‎13．如图所示，将两个质量均为m的小球a、b用细线相连悬挂于O点，两绳可承受的最大张力为3.5mg．先用力F拉住小球a，使整个装置处于平衡状态，并保持悬线Oa与竖直方向的夹角为θ=30°不变，则F的大小可能为（　　）‎ A． mg B．mg C． mg D．3mg ‎【考点】共点力平衡的条件及其应用；物体的弹性和弹力．‎ ‎【分析】对两个球整体受力分析，受重力、拉力F和细线的拉力T，根据平衡条件并结合合成法作图分析得到拉力的范围即可．‎ ‎【解答】解：对小球a、b整体受力分析，如图所示：‎ 当拉力F的方向改变时，重力不变，拉力T的方向不改变，结合三角形定则作图，如图所示：‎ 当拉力T=3.5mg时，拉力F最小，结合余弦定理，有：‎ Fmax=≈2mg 当拉力F垂直细线oa时，拉力最小，为：‎ Fmin=（2mg）sin30°=mg A、mg＜Fmin，故A错误；‎ B、mg=Fmin，故B正确；‎ C、Fmax＞mg＞Fmin，故C正确；‎ D、3mg＞Fmax，故D错误；‎ 故选：BC ‎　‎ ‎14．在平直公路上，汽车以10m/s的速度匀速驶向路口，当行驶至距路口停车线20m处时，还有3s绿灯就要熄灭．而该汽车在绿灯熄灭时刚好停在停车线处，则汽车运动的速度﹣时间图象可能是图中的（　　）‎ A． B． C． D．‎ ‎【考点】匀变速直线运动的图像；匀变速直线运动的速度与时间的关系．‎ ‎【分析】此题应先根据V﹣t图象所围成的面积表示位移，来计算或估算位移的大小．‎ ‎【解答】解：A、由图形面积表示位移知SA=（×3）m=15m，故A错误；‎ B、由图面积可知SB＞15m，故B正确；‎ C、由图形面积表示位移：SC=（10×1+×2）=20m，故C正确；‎ D、SD=（10×0.5+×2.5）m=17.5m，故D错误；‎ 故选：B、C．‎ ‎　‎ ‎15．一物体做匀加速直线运动，在 2s 内通过的位移为 6m，在紧接着的 1s 内通过的位移也为 6m．则物体运动的初速度v0和加速度a的大小（　　）‎ A．v0=1m/s B．v0=2m/s C．a=1m/s2 D．a=2m/s2‎ ‎【考点】匀变速直线运动的位移与时间的关系；匀变速直线运动规律的综合运用．‎ ‎【分析】根据匀变速直线运动的公式，根据前2s内的位移为6m，列出表达式，含有v0和a两个未知量，再根据前3s内的位移为12m，再列出表达式，也含有v0和a两个未知量，联立方程组求解，得出初速度和加速度a．‎ ‎【解答】解：设物体的初速度为v0，通过第一段位移x时，由匀变速直线运动的位移公式得：‎ ‎…①‎ 通过两段位移2x时，由匀变速直线运动的位移公式得：‎ ‎2x=…②‎ 联立解得：a=…③‎ 代入数据：v0=1m/s，a=2m/s2．‎ 故选：AD ‎　‎ ‎16．某司机在检测汽车性能过程中，得到汽车减速过程中的位移s与速度v的关系曲线如图所示，并得出位移s与速度v的函数关系式为s=m﹣nv2，其中m、n为常数．重力加速度的大小g取10m/s2．则以下判断正确的是（　　）‎ A．汽车在此过程中做匀变速直线运动 B．汽车的末速度为20m/s C．由题中所给已知条件可确定m、n的大小 D．汽车对司机作用力的大小与司机重力大小的比值为 ‎【考点】牛顿第二定律．‎ ‎【分析】根据速度与位移的函数关系确定汽车的运动规律，汽车做匀减速运动，末速度为零，根据速度位移公式，结合位移与速度的函数表达式求出m和n．根据牛顿加速度的大小分析作用力与重力的大小比值．‎ ‎【解答】解：A、由位移与速度的函数关系式可知，汽车在此过程中做匀变速直线运动，故A正确；‎ B、汽车做匀减速直线运动，汽车末速度为0，故B错误；‎ C、把坐标轴上的（0，25m）和（72km/h，0），单位换算后代入v2=2as，可求m=25，n=，故C正确；‎ D、加速度，可知合力大小与重力大小的比值为4：5，而作用力的大小与合力大小不等，故D错误．‎ 故选：AC．‎ ‎　‎ 二、实验题：本题共2小题，共12分 ‎17．如图所示是某同学在做匀变速直线运动实验中获得的一条纸带，打点计时器电源频率为50Hz，A、B、C、D是纸带上四个计数点，每两个相邻计数点间有四个点没有画出．从图中读出A、B两点间距x=　0.70　cm；B点对应的速度是　0.080　m/s；物体运动的加速度是　0.20　m/s2．（计算结果保留二位有效数字）．‎ ‎【考点】探究小车速度随时间变化的规律．‎ ‎【分析】根据某段时间内的平均速度等于中间时刻的瞬时速度求出B点的速度，根据连续相等时间内的位移之差是一恒量求出物体运动的加速度．‎ ‎【解答】解：由图可知，A、B两点间的距离x=0.70cm，B点的瞬时速度=0.080m/s．‎ 因为连续相等时间内的位移之差△x=0.20cm，根据△x=aT2得，加速度a=．‎ 故答案为：0.70，0.080，0.20，‎ ‎　‎ ‎18．橡皮筋也像弹簧一样，在弹性限度内，伸长量x与弹力F成正比，即F=kx，k的值与橡皮筋未受到拉力时的长度L、横截面积S有关，理论与实践都表明k=Y，其中Y是一个由材料决定的常数，材料力学上称之为杨氏模量．‎ ‎（1）在国际单位制中，杨氏模量Y的单位应该是　D　‎ A．N B．m C．N/m D．Pa ‎（2）有一段横截面是圆形的橡皮筋，应用如图所示的实验装置可以测量出它的杨氏模量Y的值．首先利用测量工具a测得橡皮筋的长度L=20.00cm，利用测量工具b测得橡皮筋未受到拉力时的直径D=4.000mm，那么测量工具a应该是　毫米刻度尺　，测量工具b应该是　螺旋测微器　．‎ ‎（3）下面的表格是橡皮筋受到的拉力F与伸长量x的实验记录．‎ 拉力F/N ‎5‎ ‎10‎ ‎15‎ ‎20‎ ‎25‎ 伸长量x/cm ‎1.6‎ ‎3.2‎ ‎4.7‎ ‎6.4‎ ‎8.0‎ 可求得该橡皮筋的劲度系数k=　3.1×102　N/m．‎ ‎（4）这种橡皮筋的Y值等于　5×106 Pa　．‎ ‎【考点】探究弹力和弹簧伸长的关系．‎ ‎【分析】根据表达式k=Y推导出Y的单位．‎ 根据所要测量的长度大小选择适合的仪器．‎ 根据记录的数据，分别在坐标上找出对应的点，连线即可；‎ 根据胡克定律写出F与x的方程即可正确解答．‎ ‎【解答】解：（1）根据表达式k=Y得：‎ Y=‎ 已知K的单位是N/m，L的单位m，S的单位是m2，‎ 所以Y的单位是N/m2，也就是Pa 故选D．‎ ‎（2）测得橡皮筋的长度L用毫米刻度尺．测量工具橡皮筋未受到拉力时的直径用螺旋测微器．‎ ‎（3）由描点法作出图象如图所示；‎ 根据F=kx可知，图象的斜率大小等于劲度系数大小，由图象求出劲度系数为k=3.1×102　N/m．‎ ‎（4）根据表示出Y Y===5.0×106Pa．‎ 故答案：（1）D；（2）毫米刻度尺，螺旋测微器；（3）图象见解析图，3.1×102；（4）5×106 Pa ‎　‎ 三、计算题：本题共4小题，共40分．要求写出必要的文字说明、主要方程式和重要演算步骤，有数值计算的要明确写出数值和单位，只有最终结果的不得分．‎ ‎19．如图所示，用一根轻质、光滑且不可伸长的绳子晾晒衣服，绳长L，绳子的两端分别固定在间距为d的两根竖直杆上（已知L＞d），衣服及衣服撑的总质量为m，重力加速度为g，当利用衣服撑把衣服挂到此绳子上静止后，求此时绳子的张力大小．‎ ‎【考点】共点力平衡的条件及其应用；物体的弹性和弹力．‎ ‎【分析】对挂钩受力分析，根据平衡条件结合几何关系列式求解．根据三力平衡条件可知，两绳子的拉力T的合力F与mg等值反向．‎ ‎【解答】解：设绳子与水平方向的夹角为θ，则由数学知识可得：‎ cosθ=‎ sinθ=‎ 根据平衡条件，有：‎ ‎2Tsinθ=mg 解得：‎ T=‎ 答：此时绳子的张力大小为．‎ ‎　‎ ‎20．如图所示，质量为m的物体，放在一固定斜面上，当斜面倾角为θ=30°时恰能沿斜面匀速下滑．重力加速度为g．‎ ‎（1）物体与斜面间的动摩擦因数μ；‎ ‎（2）现对物体施加一大小为F的水平向右恒力，使物体可沿斜面匀速向上滑行．求F的大小（用m、g、θ表示）．（要求画出受力分析图）‎ ‎（3）设最大静摩擦力等于滑动摩擦力，当斜面倾角增大并超过某一临界角θ0时，不论水平恒力F多大，都不能使物体沿斜面向上滑行．求这一临界角θ0的大小．‎ ‎【考点】牛顿第二定律；物体的弹性和弹力．‎ ‎【分析】（1）匀速下滑，根据共点力平衡求得摩擦因数；‎ ‎（2）匀速上滑，根据共点力平衡求得推力；‎ ‎（3）本题两次平衡问题，运用平衡条件分析研究两次，实质上滑动摩擦力大小没有变化，但方向相反 ‎【解答】解：（1）物体匀速下滑，根据共点力平衡可知：mgsinθ=μmgcosθ ‎ 解得：μ=tanθ=‎ ‎（2）物体沿斜面匀速上升时，根据平衡条件有：‎ Fcosθ=mgsinθ+f FN=Fsinθ+mgcosθ f=μFN 联立解得：F=‎ ‎（3）依题意，不论水平恒力F多大，都不能使物体沿斜面向上滑行，即：‎ F=中，F→∝‎ 故应有 cosθ0﹣μsinθ0=0，则 可知 θ0=60°‎ 答：（1）物体与斜面间的动摩擦因数μ为；‎ ‎（2）F的大小为 ‎（3）这一临界角θ0的大小为60°‎ ‎　‎ ‎21．据英国《每日邮报》报道，英国触式橄榄球球员赫普顿斯托尔在伦敦成功挑战地铁速度．他从“市长官邸站”下车，在下一地铁站“坎农街站”在车门快关上前成功跑回同一节车厢．‎ 已知西安地铁一号线某两站间距离约为x=600m，地铁列车每次停站时间（从车门打开到关闭的时间）为ta=45s，列车加速和减速的加速度大小均为a=1m/s2，运行过程的最大速度为vm=54km/h．假设列车运行过程中只做匀变速和匀速运动，两站之间的地铁轨道和地面道路都是平直的且长度相同，出站和进站最短共需用时tb=70s． 若有人想在这两个地铁车站间挑战地铁速度，他在地面道路上奔跑的平均速度至少多大？‎ ‎【考点】匀变速直线运动的位移与时间的关系；匀变速直线运动的速度与时间的关系．‎ ‎【分析】根据速度时间公式求出加速和减速的时间，然后减去题目告知的出站进站时间，由速度位移公式求出加速和减速过程的位移，即可得到匀速运动的位移，求得匀速运动的时间，即可得到总时间，从而求出奔跑的平均速度．‎ ‎【解答】解：列车运行过程的最大速度为：vm=54km/h=15m/s 列车从静止加速到最大速度过程所用时间为：t1==s=15s ‎ 运动的位移为：x1==112.5m 根据对称性可知，列车从最大速度减速到0的时间为：t2=t1=15s，‎ 位移为：x2=x1=112.5m 可见，列车以最大速度匀速运动的时间为：t3==25s 挑战者在地面道路奔跑的最长时间为：t=2ta+t1+t2+t3﹣tb=75s 最小平均速度为： ===8m/s 答：他在地面道路上奔跑的平均速度至少是8m/s．‎ ‎　‎ ‎22．甲、乙两车在平直公路上比赛，某一时刻，乙车在甲车前方L1=11m处，乙车速度v乙=60m/s，甲车速度v甲=50m/s，此时乙车离终点线尚有L2=600m，如图所示．若甲车做匀加速运动，加速度a=2m/s2，乙车速度不变，不计车长．‎ ‎（1）经过多长时间甲、乙两车间距离最大，最大距离是多少？‎ ‎（2）到达终点时甲车能否超过乙车？‎ ‎【考点】匀变速直线运动的位移与时间的关系；匀变速直线运动的速度与时间的关系．‎ ‎【分析】（1）抓住两车相距最大时的临界条件：两车速度相等展开计算即可；‎ ‎（2）分析甲车追上乙车时，两车位移关系，求出相遇时的时间，再求出乙车到达终点的时间，比较即可求解．‎ ‎【解答】解：（1）当甲、乙两车速度相等时，两车间距离最大，即v甲+at1=v乙，‎ 得t1==s=5s；‎ 甲车位移x甲=v甲 t1+at2=275 m，‎ 乙车位移x乙=v乙 t1=60×5 m=300 m，‎ 此时两车间距离△x=x乙+L1﹣x甲=36 m ‎（2）甲车追上乙车时，位移关系为 x甲′=x乙′+L1，‎ 甲车位移x甲′=v甲 t2+at22，‎ 乙车位移x乙′=v乙 t2，‎ 将x甲′、x乙代入位移关系，得 v甲t2+at2=v乙t2+L1，‎ 代入数据t2=11s，‎ 实际乙车到达终点的时间为t3=，‎ 所以到达终点时甲车不能超过乙车．‎ 答：（1）经过5s甲、乙两车间距离最大，最大距离是36 m；‎ ‎（2）到达终点时甲车不能超过乙车．‎ ‎　‎ ‎2017年3月15日