2019年高考数学考纲解读与热点难点突破专题14空间中的平行与垂直（热点难点突破）理（含解析） 10页

空间中的平行与垂直 ‎1.四棱锥PABCD的三视图如图所示，四棱锥PABCD的五个顶点都在一个球面上，E，F分别是棱AB，CD的中点，直线EF被球面所截得的线段长为2，则该球的表面积为(　　)‎ A．12π B．24π C．36π D．48π 答案　A ‎2．已知a，b，m，n是四条不同的直线，其中a，b是异面直线，则下列命题正确的个数为(　　)‎ ‎①若m⊥a，m⊥b，n⊥a，n⊥b，则m∥n ‎②若m∥a，n∥b，则m，n是异面直线 ‎③若m与a，b都相交，n与a，b都相交，则m，n是异面直线 A．0 B．1‎ C．2 D．3‎ 解析　显然①正确．②中m，n可能异面，可能相交，∴②不正确．③中m，n可能异面，可能相交，∴③不正确．‎ 答案　B ‎3．已知l，m，n是空间中的三条直线，命题p：若m⊥l，n⊥l，则m∥n；命题q：若直线l，m，n两两相交，则直线l，m，n共面，则下列命题为真命题的是(　　)‎ A．p∧q B．p∨q C．p∨(非q) D．(非p)∧q 10‎ 解析　命题p中，m，n可能平行，还可能相交或异面，所以命题p为假命题；命题q中，当三条直线交于三个不同的点时，三条直线一定共面，当三条直线交于一点时，三条直线不一定共面，所以命题q也为假命题．所以非p和非q都为真命题，故p∨(非q)为真命题．‎ 答案　C ‎4．设α，β是两个不同的平面，l是一条直线，以下命题：‎ ‎①若l⊥α，α⊥β，则l∥β；②若l∥α，α∥β，则l∥β；‎ ‎③若l⊥α，α∥β，则l⊥β；④若l∥α，α⊥β，则l⊥β.‎ 其中正确命题的个数是(　　)‎ A．1 B．2‎ C．3 D．4‎ 解析　对于①，可能l⊂β，对于②，可能l⊂β；对于④，l∥β，l⊂β，l与β相交都有可能．综上可知①②④为假命题．由面面平行的性质定理易知命题③正确，故选A. 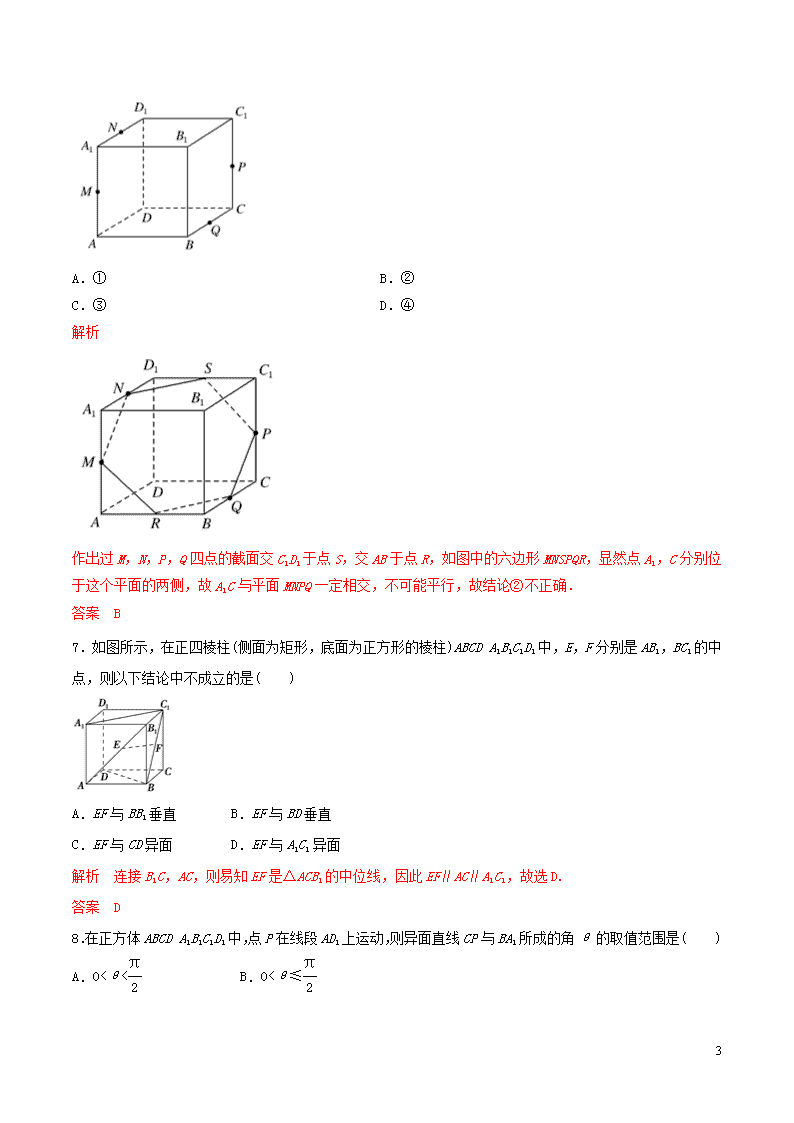‎ 答案　A ‎5.如图，正方体ABCD－A1B‎1C1D1中，E是棱B‎1C1的中点，动点P在底面ABCD内，且PA1＝A1E，则点P运动形成的图形是(　　)‎ A．线段 B．圆弧 C．椭圆的一部分 D．抛物线的一部分 解析　由PA1＝A1E知点P应落在以A1为球心，A1E长为半径的球面上．又知动点P在底面ABCD内，所以点P的轨迹是底面ABCD与球面形成的交线，故为圆弧，所以选B.‎ 答案　B ‎6.如图所示，在正方体ABCD－A1B‎1C1D1中，M，N，P，Q分别是AA1，A1D1，CC1，BC的中点，给出以下四个结论：①A‎1C⊥MN；②A‎1C∥平面MNPQ；③A‎1C与PM相交；④NC与PM异面．其中不正确的结论是(　　)‎ 10‎ ‎ ‎ A．① B．②‎ C．③ D．④‎ 解析　‎ 作出过M，N，P，Q四点的截面交C1D1于点S，交AB于点R，如图中的六边形MNSPQR，显然点A1，C分别位于这个平面的两侧，故A‎1C与平面MNPQ一定相交，不可能平行，故结论②不正确． ‎ 答案　B ‎7．如图所示，在正四棱柱(侧面为矩形，底面为正方形的棱柱)ABCDA1B1C1D1中，E，F分别是AB1，BC1的中点，则以下结论中不成立的是(　　)‎ A．EF与BB1垂直 B．EF与BD垂直 C．EF与CD异面 D．EF与A1C1异面 解析　连接B1C，AC，则易知EF是△ACB1的中位线，因此EF∥AC∥A1C1，故选D.‎ 答案　D ‎8．在正方体ABCDA1B1C1D1中，点P在线段AD1上运动，则异面直线CP与BA1所成的角θ的取值范围是(　　)‎ A．0<θ< B．0<θ≤ 10‎ C．0≤θ≤ D．0<θ≤ 解析　当P在D1处时，CP与BA1所成角为0；‎ 当P在A处时，CP与BA1所成角为，∴0<θ≤.‎ 答案　D ‎9．设m，n是两条不同的直线，α，β，γ是三个不同的平面，给出下列四个命题：‎ ‎①m⊥α，n∥α，则m⊥n；②若α⊥γ，β⊥γ，则α∥β；③若α∥β，β∥γ，m⊥α，则m⊥γ；④若α∩γ＝m，β∩γ＝n，m∥n，则α∥β.‎ 其中正确命题的序号是(　　)‎ A．①和③ B．②和③ C．③和④ D．①和④‎ 解析　②中平面α，β可能相交；④平面α，β可能相交，故选A.‎ 答案　A ‎10． a、b、c为三条不重合的直线，α、β、γ为三个不重合的平面，现给出六个命题：‎ ‎①⇒a∥b；②⇒a∥b；‎ ‎③⇒α∥β；④⇒α∥β；‎ ‎⑤⇒α∥a；⑥⇒a∥α.‎ 其中正确的命题是(　　)‎ A．①②③ B．①④⑤ C．①④ D．①③④‎ 解析　①④正确．②错，a、b可能相交或异面．③错，α与β可能相交．⑤⑥错，a可能在α内．‎ 答案　C ‎11.正三棱锥的高为1，底面边长为2，内有一个球与它的四个面都相切(如图)．求：‎ ‎ (1)这个正三棱锥的表面积；‎ 10‎ ‎(2)这个正三棱锥内切球的表面积与体积．‎ 解　(1)底面正三角形中心到一边的距离为××2＝， ‎ 则正棱锥侧面的斜高为＝.‎ ‎∴S侧＝3××2×＝9.‎ ‎∴S表＝S侧＋S底＝9＋××(2)2‎ ‎＝9＋6.‎ ‎(2)设正三棱锥PABC的内切球球心为O，连接OP，OA，OB，OC，而O点到三棱锥的四个面的距离都为球的半径r.‎ ‎∴VPABC＝VOPAB＋VOPBC＋VOPAC＋VOABC ‎＝S侧·r＋S△ABC·r＝S表·r ‎＝(3＋2)r.‎ 又VPABC＝×××(2)2×1＝2，‎ ‎∴(3＋2)r＝2，‎ 得r＝＝＝－2.‎ ‎∴S内切球＝4π(－2)2＝(40－16)π.‎ V内切球＝π(－2)3＝(9－22)π.‎ ‎12．如图所示，在边长为5＋的正方形ABCD中，以A为圆心画一个扇形，以O为圆心画一个圆，M，N，K为切点，以扇形为圆锥的侧面，以圆O为圆锥底面，围成一个圆锥，求圆锥的表面积与体积．‎ 解　设圆锥的母线长为l，底面半径为r，高为h，‎ 由已知条件得 解得r＝，l＝4.所以S＝πrl＋πr2＝10π，h＝＝，‎ V＝πr2h＝.‎ 10‎ ‎13.在空间四边形ABCD中，已知AD＝1，BC＝，且AD⊥BC，对角线BD＝，AC＝，求AC和BD所成的角．‎ 解　如图，分别取AD，CD，AB，BD的中点E，F，G，H，连接EF，FH，HG，GE，GF.‎ 由三角形的中位线定理知，EF∥AC，‎ 且EF＝，GE∥BD，且GE＝.‎ GE和EF所成的锐角(或直角)就是AC和BD所成的角．‎ 同理，GH＝，HF＝，GH∥AD，HF∥BC.‎ 又AD⊥BC，∴∠GHF＝90°， ‎ ‎∴GF2＝GH2＋HF2＝1.‎ 在△EFG中，EG2＋EF2＝1＝GF2，‎ ‎∴∠GEF＝90°，即AC和BD所成的角为90°.‎ ‎14．已知空间四边形ABCD中，E，H分别是边AB，AD的中点，F，G分别是边BC，CD的中点．‎ ‎(1)求证：BC与AD是异面直线；‎ ‎(2)求证：EG与FH相交．‎ 证明　(1)假设BC与AD共面．‎ 不妨设它们所共平面为α，则B，C，A，D∈α.‎ ‎∴四边形ABCD为平面图形，‎ 这与四边形ABCD为空间四边形相矛盾，‎ ‎∴BC与AD是异面直线．‎ ‎(2)如图，连接AC，BD，‎ 则EF∥AC，HG∥AC，‎ ‎∴EF∥HG.同理，EH∥FG，‎ 则EFGH为平行四边形．‎ 又EG，FH是▱EFGH的对角线，‎ ‎∴EG与HF相交．‎ ‎15．如图，圆O为三棱锥P－ABC的底面ABC的外接圆，AC是圆O的直径，PA⊥BC，点M是线段PA的中点．‎ 10‎ ‎ (1)求证：BC⊥PB；‎ ‎(2)设PA⊥AC，PA＝AC＝2，AB＝1，求三棱锥P－MBC的体积；‎ ‎(3)在△ABC内是否存在点N，使得MN∥平面PBC？请证明你的结论．‎ ‎(1)证明　如图，因为AC是圆O的直径，所以BC⊥AB，‎ 因为BC⊥PA，又PA、AB⊂平面PAB，且PA∩AB＝A，‎ 所以BC⊥平面PAB，又PB⊂平面PAB，所以BC⊥PB，‎ ‎(2)解　如图，在Rt△ABC中，AC＝2，AB＝1，‎ 所以BC＝，‎ 因此S△ABC＝，‎ 因为PA⊥BC，PA⊥AC，BC∩AC＝C，‎ 所以PA⊥平面ABC，‎ 所以，VP－MBC＝VP－ABC－VM－ABC＝··2－··1＝.‎ ‎(3)解　如图，取AB的中点D，连接OD、MD、OM，则N为线段OD(除端点O、D外)上任意一点即可，理由如下：‎ 因为M、O、D分别是PA、AC、AB的中点，所以MD∥PB，MO∥PC.因为，MD⊄平面PBC，PB⊂平面PBC，‎ 所以MD∥平面PBC，同理可得，MO∥平面PBC.‎ 因为MD、MO⊂平面MDO，MD∩MO＝M，‎ 所以平面MDO∥平面PBC，‎ 因为MN⊂平面MDO，故MN∥平面PBC.‎ ‎16.如图，已知四棱锥P－ABCD，底面ABCD是等腰梯形，且AB∥CD，O是AB中点，PO⊥平面ABCD，PO＝CD＝DA＝AB＝4，M是PA中点．‎ 10‎ ‎(1)证明：平面PBC∥平面ODM；‎ ‎(2)求点A到平面PCD的距离．‎ 解　(1)证明：由题意，CD∥BO，CD＝BO，‎ ‎∴四边形OBCD为平行四边形，∴BC∥OD.‎ 又∵AO＝OB，AM＝MP，∴OM∥PB.‎ 又OM⊄平面PBC，PB⊂平面PBC，‎ ‎∴OM∥平面PBC.‎ 同量，OD∥平面PBC，又OM∩OD＝O，‎ ‎∴平面PBC∥平面ODM.‎ ‎(2)取CD的中点N，连接ON，PN，则ON，PN分别为△ACD，△PCD的高．‎ 由PO＝CD＝DA＝AB＝4.‎ 可得PN＝2，ON＝2.‎ 设点A到平面PCD的距离为d.‎ ‎∵V三棱锥A－PCD＝V三棱锥P－ACD，‎ 即××4×2×d＝××4×2×4，‎ ‎∴d＝.‎ ‎17.如图，在三棱柱ABC－A1B‎1C1中，侧棱垂直于底面，AB⊥BC，AA1＝AC＝2，BC＝1，E，F分别是A‎1C1，BC的中点．‎ 10‎ ‎(1)求证：平面ABE⊥平面B1BCC1；‎ ‎(2)求证：C‎1F∥平面ABE；‎ ‎(3)求三棱锥E－ABC的体积．‎ 解　‎ 因为AC∥A‎1C1，且AC＝A‎1C1，‎ 所以FG∥EC1，且FG＝EC1.‎ 所以四边形FGEC1为平行四边形．‎ 所以C‎1F∥EG.‎ 又因为EG⊂平面ABE，C‎1F⊄平面ABE，‎ 所以C‎1F∥平面ABE.‎ 10‎ ‎(3)因为AA1＝AC＝2，BC＝1，AB⊥BC，‎ 所以AB＝＝.‎ 所以三棱锥E－ABC的体积 V＝S△ABC·AA1＝×××1×2＝. ‎ 10‎