2019届二轮复习第4课力的合成与分解课件（32张）（全国通用） 32页

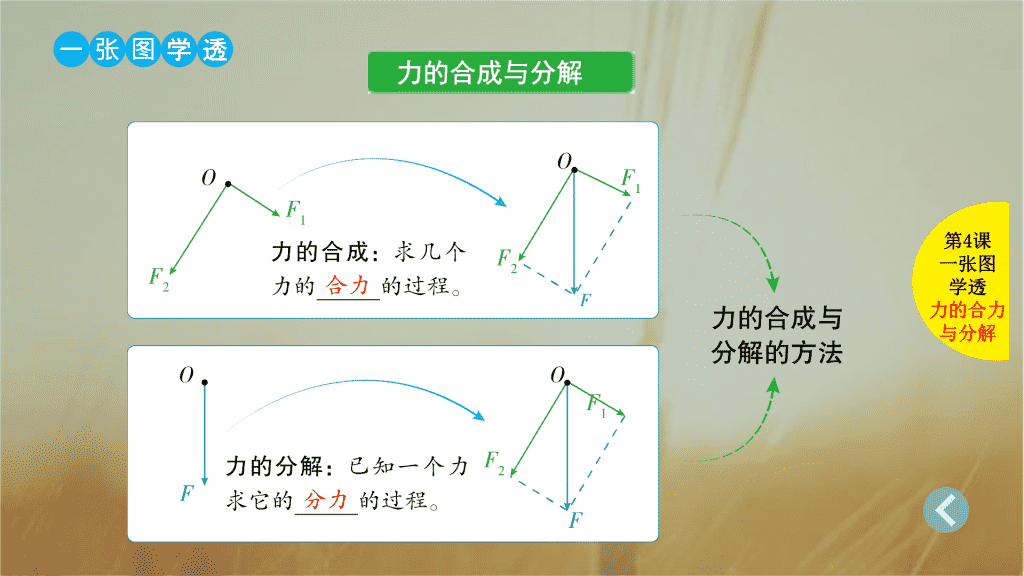
第 4 课 力的合成 与分解 普查 讲 4 一张图学透 两组 题讲透 第 （ 2 ） 题 第 （ 4 ） 题 目录 第 （ 1 ） 题 第 （ 3 ） 题 第 （ 5 ） 题 合力、分力 力的合成与分解 第 4 课 一张图 学透 合力、 分力 一 张 图 学 透 合力、分力 一 张 图 学 透 力的合成与分解 第 4 课 一张图 学透 力的合力 与分解 一 张 图 学 透 第 4 课 一张图 学透 力的合力 与分解 力的合成与分解 第 4 课 第 （ 1 ） 题 P19 ( 1 ) 三 个共面的共点力大小分别是 F 1 、 F 2 、 F 3 ，关于它们的合力 F 的大小，下列说法中正确的是 ( ) A. 无论 F 1 、 F 2 、 F 3 如何取值， F 大小的取值范围一定是 0≤ F ≤ F 1 ＋ F 2 ＋ F 3 B. F 至少比 F 1 、 F 2 、 F 3 中的某一个大 C. 若 F 1 ∶ F 2 ∶ F 3 ＝ 3∶6∶8 ，只要适当调整它们之间的夹角，一定能使合力 F 为 0 D. 若不能通过平移使三个力组成三角形，则它们的合力 F 一定不为 0 两 组 题 讲 透 解析 ： 三个共点力的合力的最小值能否为零 , 取决于任何一个力是否都在其余两个力的合力范围内 , 由于三个力大小未知 , 所以三个力的合力的最小值不一定为 0, 故 A 项错误。合力不一定大于分力 , 故 B 项错误。当三个力的大小分别为 3 a 、 6 a 、 8 a 时 , 其中任何一个力都在其余两个力的合力范围内 , 故 C 项正确。当三个力共线时 , 它们不能通过平移组成三角形 , 但是它们的合力可能为 0, 故 D 项错误。 两 组 题 讲 透 第 4 课 第 （ 1 ） 题 P19 两 组 题 讲 透 ( 1 ) 三 个共面的共点力大小分别是 F 1 、 F 2 、 F 3 ，关于它们的合力 F 的大小，下列说法中正确的是 ( ) A. 无论 F 1 、 F 2 、 F 3 如何取值， F 大小的取值范围一定是 0≤ F ≤ F 1 ＋ F 2 ＋ F 3 B. F 至少比 F 1 、 F 2 、 F 3 中的某一个大 C. 若 F 1 ∶ F 2 ∶ F 3 ＝ 3∶6∶8 ，只要适当调整它们之间的夹角，一定能使合力 F 为 0 D. 若不能通过平移使三个力组成三角形，则它们的合力 F 一定不为 0 C 第 4 课 第 （ 1 ） 题 P19 两 组 题 讲 透 图示 小积累 力的合成中合力与分力的大小 第 4 课 小积累 P19 两 组 题 讲 透 图示 小积累 力的合成中合力与分力的大小 第 4 课 小积累 P19 两 组 题 讲 透 图示 小积累 第 4 课 小积累 P19 力的合成中合力与分力的大小 两 组 题 讲 透 图示 小积累 第 4 课 小积累 P19 力的合成中合力与分力的大小 两 组 题 讲 透 图示 小积累 第 4 课 小积累 P19 力的合成中合力与分力的大小 第 4 课 第 （ 2 ） 题 P19 两 组 题 讲 透 ( 2 ) 如 图，用两根等长轻绳将木板悬挂在竖直木桩上等高的两点，制成一简易秋千。某次维修时将两轻绳各剪去一小段，但仍保持等长且悬挂点不变。木板静止时， F 1 表示木板所受合力的大小， F 2 表示单根轻绳对木板拉力的大小，则维修后 ( ) A. F 1 不变， F 2 变大 B. F 1 不变， F 2 变小 C. F 1 变大， F 2 变大 D. F 1 变小， F 2 变小 木板静止时受重力和两绳拉力平衡，故合力为 0 ，即 F 1 =0 。如图所示，由正弦定理 得 ， 解得 F 2 = 。 由题可知，剪短绳子， θ 变大，故 F 2 变大，故 A 项正确 。 两 组 题 讲 透 解析 ： 第 4 课 第 （ 2 ） 题 P19 两 组 题 讲 透 ( 2 ) 如 图，用两根等长轻绳将木板悬挂在竖直木桩上等高的两点，制成一简易秋千。某次维修时将两轻绳各剪去一小段，但仍保持等长且悬挂点不变。木板静止时， F 1 表示木板所受合力的大小， F 2 表示单根轻绳对木板拉力的大小，则维修后 ( ) A. F 1 不变， F 2 变大 B. F 1 不变， F 2 变小 C. F 1 变大， F 2 变大 D. F 1 变小， F 2 变小 A 第 4 课 第 （ 2 ） 题 P19 两 组 题 讲 透 利用力的合成解决实际问题时的一般思路 第 4 课 方法便笺 P19 两 组 题 讲 透 利用力的合成解决实际问题时的一般思路 第 4 课 方法便笺 P19 第 4 课 第 （ 3 ） 题 P19 ( 3 ) 已知 两个共点力的合力为 50 N ，分力 F 1 的方向与合力 F 的方向成 30° 角，分力 F 2 的大小为 30 N ，则 ( ) A. F 1 的大小是唯一 的 B. F 2 的方向是唯一的 C. F 2 有两个可能的 方向 D. F 2 可取任意方向 两 组 题 讲 透 由 F 1 、 F 2 和 F 的矢量三角形并结合几何关系可以看出 , 当 F 2 = F 20 =25 N 时 , F 1 的大小是唯一的。 F 2 的 方向也是唯一的。因 F 2 =30 N> F 20 =25 N, 所以 F 1 的大小有两个 , 即 F 1 ′ 和 F 1 ″, F 2 的 方向也有两个 , 即 F 2 ′ 的方向和 F 2 ″ 的方向 , 故 C 项正确。 解析 ： 两 组 题 讲 透 第 4 课 第 （ 3 ） 题 P19 两 组 题 讲 透 ( 3 ) 已知 两个共点力的合力为 50 N ，分力 F 1 的方向与合力 F 的方向成 30° 角，分力 F 2 的大小为 30 N ，则 ( ) A. F 1 的大小是唯一 的 B. F 2 的方向是唯一的 C. F 2 有两个可能的 方向 D. F 2 可取任意方向 C 第 4 课 第 （ 3 ） 题 P19 两 组 题 讲 透 讨论分力的方向和大小 已知合力 F 的大小、方向，一个分力 F 2 的大小，求另一个分力 F 1 的大小 ( 与合力 F 的夹角 为 θ ) ，则可能出现以下几种情况 ( 图中圆的半径等于 F 2 的大小 ) 。 第 4 课 方法便笺 P19 两 组 题 讲 透 讨论分力的方向和大小 第 4 课 方法便笺 P19 ( 4 ) 重力 为 G 的物体静止在倾角为 α 的固定斜面上 , 现对物体施加一个与斜面垂直的压力 F, 如图所示 , 求物体对斜面的压力和摩擦力的大小。 两 组 题 讲 透 第 4 课 第 （ 4 ） 题 P20 将物体所受的力正交分解在垂直斜面方向与平行斜面方向 , 如图所 示 平行斜面方向 , 物体所受的摩擦力 大小 f = G sin α 垂直斜面方向 , 物体所受的支持力 大小 F N = F + G cos α 由牛顿第三定律得物体对斜面的压力 大小 F N ′= F N = F + G cos α ，物体对斜面的摩擦力 大小 f ′= f = G sin α 解析 ： 两 组 题 讲 透 答案 : F + G cos α ； G sin α 第 4 课 第 （ 4 ） 题 P20 两 组 题 讲 透 图示 第 4 课 小积累 P20 (5)( 多选 ) 如 图所示，用轻绳 OA 、 OB 和 OC 将重为 G 的重物悬挂在水平天花板和竖直墙壁之间处于静止状态， AO 绳 水平， OB 绳 与竖直方向的夹角为 θ 。则 AO 绳 的拉力 F A 、 OB 绳 的拉力 F B 的大小与 G 之间的关系为 ( ) A. F A ＝ G tan θ B. F A ＝ C. F B ＝ D. F B ＝ G cos θ 两 组 题 讲 透 第 4 课 第 （ 5 ） 题 P20 法一 ( 力的作用效果分解法 ) 以结点 O 为研究对象，绳子 OC 的 拉力 F C 等于重物重力 G 。将 F C 沿 AO 和 BO 方向分解 , 两个分力分别为 F A ′ 、 F B ′ , 如图 (a) 所示 , 可 得 =tan θ , =cos θ , 又 F A ′ = F A , F B ′ = F B , 所以 F A = G tan θ , F B = , 故 A 项、 C 项均正确 。 两 组 题 讲 透 解析 ： 第 4 课 第 （ 5 ） 题 P20 法 二 ( 正交分解法 ) 结点 O 受到三个力作用 F A 、 F B 、 F C , 如图 (b) 所示。 由水平方向受力平衡和竖直方向受 力平衡 , 列 方程 得 F B cos θ = F C = G , F B sin θ = F A ，解得 F A = G tan θ , F B = ， 故 A 项、 C 项均正确。 两 组 题 讲 透 解析 ： 第 4 课 第 （ 5 ） 题 P20 两 组 题 讲 透 (5)( 多选 ) 如 图所示，用轻绳 OA 、 OB 和 OC 将重为 G 的重物悬挂在水平天花板和竖直墙壁之间处于静止状态， AO 绳 水平， OB 绳 与竖直方向的夹角为 θ 。则 AO 绳 的拉力 F A 、 OB 绳 的拉力 F B 的大小与 G 之间的关系为 ( ) A. F A ＝ G tan θ B. F A ＝ C. F B ＝ D. F B ＝ G cos θ AC 第 4 课 第 （ 5 ） 题 P20 两 组 题 讲 透 利用力的分解解决问题的一般思路 第 4 课 方法便笺 P20 两 组 题 讲 透 利用力的分解解决问题的一般思路 第 4 课 方法便笺 P20 两 组 题 讲 透 利用力的分解解决问题的一般思路 第 4 课 方法便笺 P20