【物理】2020高考二轮复习专题练专题5动量定理动量守恒定律（解析版） 13页

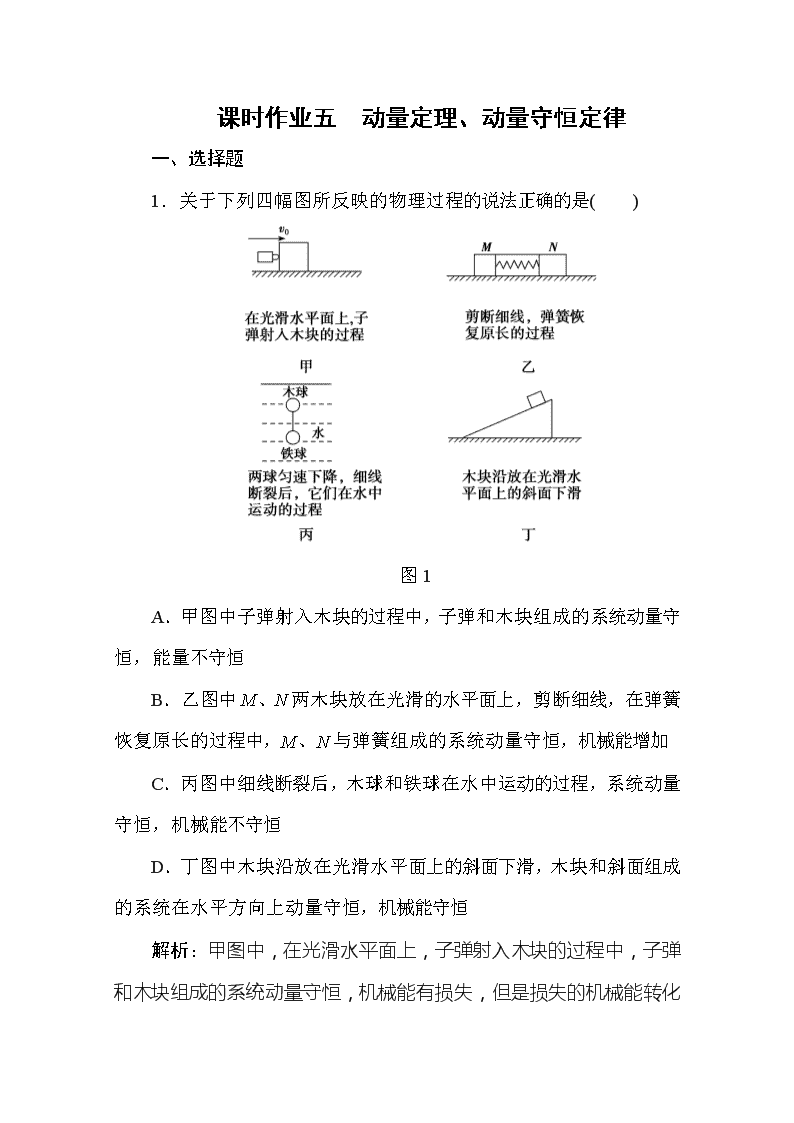
课时作业五　动量定理、动量守恒定律 一、选择题 ‎1．关于下列四幅图所反映的物理过程的说法正确的是(　　)‎ 图1‎ A．甲图中子弹射入木块的过程中，子弹和木块组成的系统动量守恒，能量不守恒 B．乙图中M、N两木块放在光滑的水平面上，剪断细线，在弹簧恢复原长的过程中，M、N与弹簧组成的系统动量守恒，机械能增加 C．丙图中细线断裂后，木球和铁球在水中运动的过程，系统动量守恒，机械能不守恒 D．丁图中木块沿放在光滑水平面上的斜面下滑，木块和斜面组成的系统在水平方向上动量守恒，机械能守恒 解析：甲图中，在光滑水平面上，子弹射入木块的过程中，子弹和木块组成的系统动量守恒 ‎，机械能有损失，但是损失的机械能转化为内能，能量仍守恒，A错误；乙图中，剪断细线，在弹簧恢复原长的过程中，M、N与弹簧组成的系统动量守恒，弹簧的弹性势能转化为木块的动能，系统机械能守恒，B错误；丙图中，木球和铁球组成的系统匀速下降，说明两球所受水的浮力等于两球自身的重力，细线断裂后两球在水中运动的过程中，所受合外力为零，系统动量守恒，由于水的浮力对两球做功，两球组成的系统机械能不守恒，选项C正确；丁图中，木块沿放在光滑水平面上的斜面下滑，木块和斜面组成的系统在水平方向上不受外力，水平方向上动量守恒，由于斜面可能不光滑，所以机械能可能有损失，D错误．‎ 答案：C ‎2．(2019年河南高三质检)甲、乙两个质量都是M的小车静置在光滑水平地面上．质量为m的人站在甲车上并以速度v(对地)跳上乙车，接着仍以对地的速率v反跳回甲车．对于这一过程，下列说法中正确的是(　　)‎ A．最后甲、乙两车的速率相等 B．最后甲、乙两车的速率之比v甲∶v乙＝M∶(m＋M)‎ C．人从甲车跳到乙车时对甲的冲量为I1，从乙车跳回甲车时对乙车的冲量为I2，应是I1＝I2‎ D．人从甲车跳到乙车时对甲的冲量为I1，从乙车跳回甲车时对乙车的冲量为I2，应是I1>I2‎ 解析：以人与甲车组成的系统为研究对象，以人的速度方向为正方向，由动量守恒定律得，人跳离甲车时，mv－Mv1＝0，‎ 以乙车与人组成的系统为研究对象，以人的速度方向为正方向，由动量守恒定律得，人跳上乙车时，mv＝(m＋M)v2，人跳离乙车时，－(m＋M)v2＝－Mv乙＋mv，以人与甲车组成的系统为研究对象，以人的速度方向为正方向，由动量守恒定律得，人反跳回甲车时，mv＋Mv1＝(m＋M)v甲，解得＝，故A错误，B正确；由动量定理得，对甲车I1＝Mv1＝mv，对乙车I2＝Mv乙－Mv2＝2mv－>mv，即I1·3m·v2，选项D错误．‎ 答案：A ‎4．2017年7月9日，斯诺克世界杯在江苏无锡落下帷幕，由丁俊晖和梁文博组成的中国A队在决赛中1比3落后的不利形势下成功逆转，最终以4比3击败英格兰队，帮助中国斯诺克台球队获得了世界杯三连冠，如图2为丁俊晖正在准备击球．设在丁俊晖这一杆中，白色球(主球)和花色球碰撞前、后都在同一直线上运动，碰前白色球的动量为pA＝5 kg·m/s，花色球静止，白色球A与花色球B发生碰撞后，花色球B的动量变为pB′＝4 kg·m/s，则两球质量mA与mB间的关系可能是(　　)‎ 图2‎ A．mB＝mA B．mB＝mA C．mB＝mA D．mB＝6mA 解析：由动量守恒定律得pA＋pB＝pA′＋pB′，解得pA′＝1 kg·m/s，根据碰撞过程中总动能不增加，则有≥＋，代入数据解得mB≥mA，碰后两球同向运动，白色球A的速度不大于花色球B的速度，则≤，解得mB≤4mA，综上可得mA≤mB≤4mA，选项A正确．‎ 答案：A ‎5．如图3所示，在光滑的水平面上，质量m1的小球A以速率v0向右运动．在小球的前方O点处有一质量为m2的小球B处于静止状态，Q点处为一竖直的墙壁．小球A与小球B发生弹性正碰后小球A与小球B均向右运动．小球B与墙壁碰撞后原速率返回并与小球A在P点相遇，PQ＝2PO，则两小球质量之比m1∶m2为(　　)‎ 图3‎ A．7∶5 B．1∶3‎ C．2∶1 D．5∶3‎ 解析：设A、B两个小球碰撞后的速度分别为v1、v2，由动量守恒定律有m1v0＝m1v1＋m2v2，发生弹性碰撞，不损失动能，故根据能量守恒定律有m1v02＝m1v12＋m2v22，两个小球碰撞后到再次相遇，其速率不变，由运动学规律有v1∶v2＝PO∶(PO＋2PQ)＝PO∶(PO＋4PO)＝1∶5，联立三式可得m1∶m2＝5∶3，D正确．‎ 答案：D ‎6．(多选)如图4所示，小车AB放在光滑水平面上，A端固定一个轻弹簧，B端粘有油泥，AB总质量为M，质量为m的木块C放在小车上，用细绳连接于小车的A端并使弹簧压缩，开始时AB和C都静止．当突然烧断细绳时，C被释放，使C离开弹簧向B端冲去，并跟B端油泥粘在一起，忽略一切摩擦，以下说法正确的是(　　)‎ 图4‎ A．弹簧伸长过程中C向右运动，同时AB也向右运动 B．C与B碰前，C与AB的速率之比为M∶m C．C与油泥粘在一起后，AB立即停止运动 D．C与油泥粘在一起后，AB继续向右运动 解析：小车、物块和弹簧组成的系统动量守恒，开始总动量为零，在弹簧伸长的过程中，C向右运动，则小车向左运动，故A错误．规定向右为正方向，在C与B碰前，根据动量守恒定律得，0＝mvC－Mv，解得vC∶v＝M∶m，故B正确；因为小车、物块和弹簧组成的系统动量守恒，开始总动量为零，当C与油泥粘在一起时，总动量仍然为零，则小车停止运动，故C正确，D错误．‎ 答案：BC ‎7．(多选)A、B两球沿一直线运动并发生正碰，如图5所示为两球碰撞前、后的位移随时间变化的图象，a、b分别为A、B两球碰前的位移随时间变化的图象，c为碰撞后两球共同运动的位移随时间变化的图象．若A球质量是m＝2 kg，则由图判断下列结论正确的是(　　)‎ 图5‎ A．碰撞前、后A球的动量变化量为4 kg·m/s B．碰撞时A球对B球所施的冲量为－4 N·s C．A、B两球碰撞前的总动量为3 kg·m/s D．碰撞中A、B两球组成的系统损失的动能为10 J 解析：根据图象可知，碰前A球的速度vA＝－3 m/s，碰前B球的速度vB＝2 m/s，碰后A、B两球共同的速度v＝－1 m/s，故碰撞前、后A球的动量变化量为ΔpA＝mv－mvA＝4 kg·m/s，选项A正确；A球的动量变化量为4 kg·m/s，则B球的动量变化为－4 kg·m/s，根据动量定理，碰撞过程中A球对B球所施的冲量为－4 N·s，选项B正确；由于碰撞过程中动量守恒，有mvA＋mBvB＝(m＋mB)v，解得mB＝ kg，故碰撞过程中A、B两球组成的系统损失的动能为ΔE＝mvA2＋mBvB2－(m＋mB)v2＝10 J，选项D正确；A、B两球碰撞前的总动量为p＝mvA＋mBvB＝(m＋mB)v＝－ kg·m/s，选项C错误．‎ 答案：ABD ‎8．(2019年山西朔州情仁一中高三月考)(多选)‎ 图6‎ 如图6所示，一质量为m的物块甲以3 m/s的速度在光滑水平面上运动，有一轻弹簧固定在其左端，另一质量也为m的物块乙以4 m/s的速度与物块甲在同一直线上相向运动，则(　　)‎ A．甲、乙两物块在弹簧压缩过程中，系统动量守恒 B．当两物块相距最近时，甲物块的速率为零 C．碰撞过程中，甲物块的速率可能为1 m/s，也可能为5 m/s D．碰撞过程中，乙物块的速率可能为2 m/s，也可能为1.7 m/s 解析：甲、乙两物块(包括弹簧)组成的系统在弹簧压缩过程中，系统所受的合外力为零，系统动量守恒，故A正确；当两物块相距最近时速度相同，取碰撞前乙的速度方向为正方向，设共同速率为v，由动量守恒定律得：mv乙－mv甲＝2mv，代入数据解得：v＝0.5 m/s，故B错误；若物块甲的速率达到5 m/s，方向与原来相同，则：mv乙－mv甲＝－mv甲′＋m乙v乙′，代入数据解得：v乙′＝6 m/s.两个物体的速率都增大，动能都增大，违反了能量守恒定律．若物块甲的速率达到5 m/s，方向与原来相反，则：mv乙－mv甲＝mv甲′＋m乙v乙′，代入数据解得：v乙′＝－4 m/s，碰撞后，乙的动能不变，甲的动能增加，系统总动能增加，违反了能量守恒定律．所以物块甲的速率不可能达到5 m/s，故C错误；甲、乙组成的系统动量守恒，选取向右为正方向，由动量守恒定律得：mv乙－mv甲＝－mv甲′＋mv乙′，碰撞结束后，系统的动能守恒，则：m甲v甲2＋m乙v乙2＝m甲v′甲2＋m乙v′乙2.代入数据解得：v甲′＝4 m/s；v乙′＝－3 m/s.可知碰撞结束后，甲与乙交换速度；碰撞过程中，乙物块的速度在4 m/s～－3 m/s之间都是可以的．所以速率可能为2 m/s，也可能为1.7 m/s，故D正确．‎ 答案：AD 二、解答题 ‎9．(2018年高考·课标全国卷Ⅰ)一质量为m的烟花弹获得动能E 后，从地面竖直升空．当烟花弹上升的速度为零时，弹中火药爆炸将烟花弹炸为质量相等的两部分，两部分获得的动能之和也为E，且均沿竖直方向运动．爆炸时间极短，重力加速度大小为g，不计空气阻力和火药的质量．求：‎ ‎(1)烟花弹从地面开始上升到弹中火药爆炸所经过的时间；‎ ‎(2)爆炸后烟花弹向上运动的部分距地面的最大高度．‎ 解：(1)设烟花弹上升的初速度为v0，由题给条件有 则E＝mv02①‎ 设烟花弹从地面开始上升到火药爆炸所用的时间为t，‎ 由运动学公式有0－v0＝－gt②‎ 联立①②式得t＝ ③‎ ‎(2)设爆炸时烟花弹距地面的高度为h1，‎ 由机械能守恒定律有E＝mgh1④‎ 火药爆炸后，烟花弹上、下两部分均沿竖直方向运动，设爆炸后瞬间其速度分别为v1和v2.‎ 由题给条件和动量守恒定律有mv12＋mv22＝E⑤‎ mv1＋mv2＝0⑥‎ 由⑥式知，烟花弹两部分的速度方向相反，向上运动部分做竖直上抛运动．设爆炸后烟花弹向上运动部分继续上升的高度为h2，由机械能守恒定律有mv12＝mgh2⑦‎ 联立④⑤⑥⑦式得，烟花弹向上运动部分距地面的最大高度为h＝h1＋h2＝⑧‎ ‎10．如图7所示，质量均为m的木板AB和滑块CD紧靠在一起静置在光滑水平面上，木板AB的上表面粗糙，滑块CD的表面是光滑的四分之一圆弧，其始端D点切线水平且与木板AB上表面相平．一可视为质点的物块P质量也为m，从木板AB的右端以初速度v0滑上木板AB，过B点时的速度为，然后滑上滑块CD，最终恰好能滑到滑块CD的最高点C处．重力加速度为g.求：‎ 图7‎ ‎(1)物块滑到B点时木板的速度v的大小；‎ ‎(2)滑块CD圆弧的半径R.‎ 解：(1)对P和木板、滑块CD组成的系统，由动量守恒定律有mv0＝m＋2mv，解得v＝.‎ ‎(2)物块P由D点滑到C点的过程中，滑块CD和物块P组成的系统在水平方向动量守恒，‎ 有m＋m＝2mv共 系统能量守恒，有 mgR＝m()2＋m()2－×2mv共2‎ 解得R＝.‎ ‎11．如图8所示，质量为mA＝3 kg的小车A以v0＝4 m/s的速度沿光滑水平面匀速运动，小车左端固定的支架通过不可伸长的轻绳悬挂质量为mB＝1 kg的小球B(可看作质点)，小球距离车面h＝0.8 m．某一时刻，小车与静止在光滑水平面上的质量为mC＝1 kg的物块C发生碰撞并粘连在一起(碰撞时间可忽略)，此时轻绳突然断裂．此后，小球刚好落入小车右端固定的沙桶中(小桶的尺寸可忽略)，不计空气阻力，重力加速度g取10 m/s2.求：‎ 图8‎ ‎(1)小车系统的最终速度大小v共；‎ ‎(2)绳未断前小球与沙桶的水平距离L；‎ ‎(3)整个过程中系统损失的机械能ΔE机损．‎ 解：(1)设系统最终速度为v共，水平方向动量守恒，有(mA＋mB)v0＝(mA＋mB＋mC)v共 代入数据解得v共＝3.2 m/s ‎(2)A与C的碰撞动量守恒，mAv0＝(mA＋mC)v1‎ 解得v1＝3 m/s，设小球下落时间为t，则h＝gt2‎ 代入数据解得t＝0.4 s 所以绳未断前小球与沙桶的水平距离为L＝(v0－v1)t 代入数据解得L＝0.4 m ‎(3)由能量守恒得ΔE机损＝mBgh＋(mA＋mB)v02－(mA＋mB＋mC)v共2‎ 代入数据解得ΔE机损＝14.4 J