2020届宁德市普通高中毕业班第一次质量检查理科数学答案_7 9页

‎2020年宁德市普通高中毕业班质量检查 数学（理科）试题参考答案及评分标准 说明：‎ ‎ 一、本解答指出了每题要考查的主要知识和能力，并给出了一种或几种解法供参考，如果考生的解法与本解法不同，可根据试题的主要考查内容比照评分标准指定相应的评分细则．‎ ‎ 二、对计算题，当考生的解答在某一部分解答未改变该题的内容和难度，可视影响的程度决定后继部分的给分，但不得超过该部分正确解答应给分数的一半；如果后继部分的解答有较严重的错误，就不再给分．‎ ‎ 三、解答右端所注分数，表示考生正确做到这一步应得的累加分数．‎ ‎ 四、只给整数分数，选择题和填空题不给中间分．‎ 一、选择题：本题考查基础知识和基本运算，每小题5分，满分60分．‎ ‎　1．B 2．A 3．A 4．B 5．C 6．D ‎　7．D 8．C 9．B 10．A 11．C 12．D 二、填空题：本题考查基础知识和基本运算，每小题5分，满分20分．‎ ‎　13． 14． 15． 16． ‎ 三、解答题：本大题共6小题，满分70分，解答须写出文字说明、证明过程和演算步骤．‎ ‎17．本小题主要考查数列及数列求和等基础知识，考查运算求解能力，考查函数与方程思想、化归与转化思想等，满分12分．‎ ‎17． 解：（1）由两式相减，得：‎ ‎，……………………………… 2分 又，，………………………………3分 当时，且，‎ 故，得（舍去），‎ ‎，………………………………4分 数列为等差数列，公差为，………………………………5分 所以 ．………………………………6分 ‎ ‎（2）由（1）及题意可得，………………………………8分 所以 ‎]………………………………10分 ‎．………………………………12分 理科数学答案与评分细则 第9页 共9页 ‎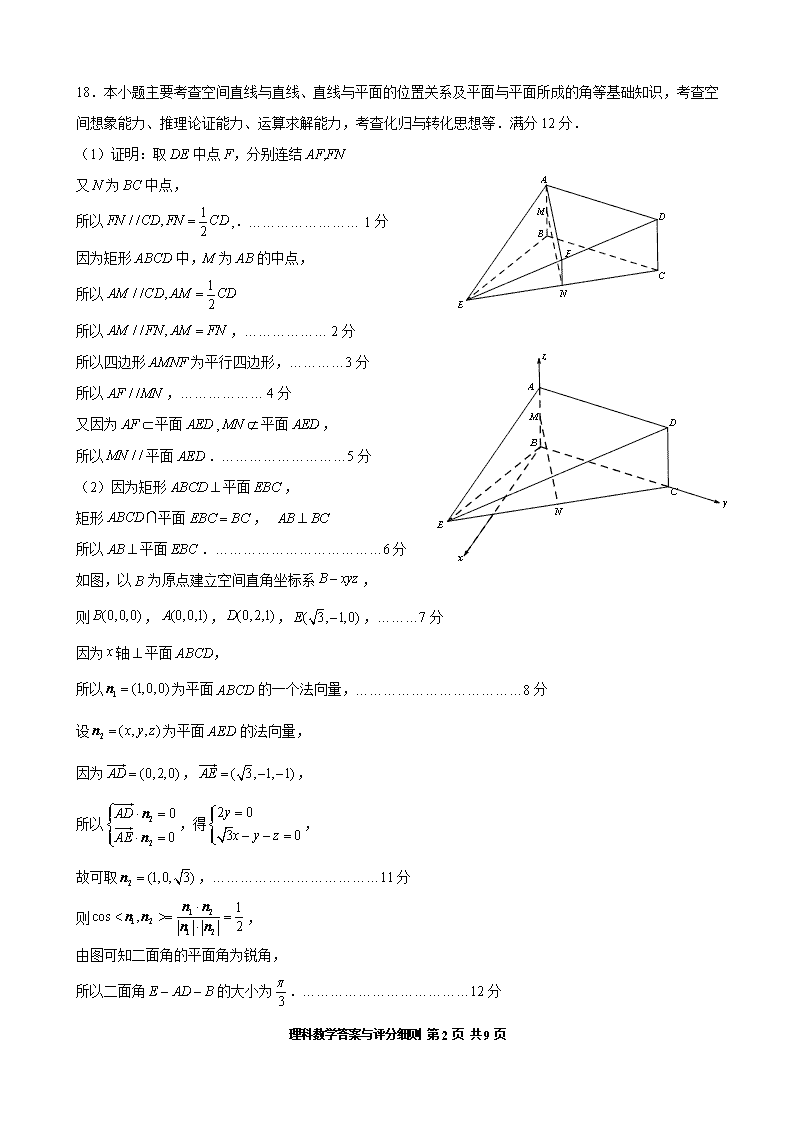18．本小题主要考查空间直线与直线、直线与平面的位置关系及平面与平面所成的角等基础知识，考查空间想象能力、推理论证能力、运算求解能力，考查化归与转化思想等．满分12分．‎ ‎（1）证明：取DE中点F，分别连结AF,FN 又N为BC中点，‎ 所以,．…………………… 1分 因为矩形ABCD中，M为AB的中点，‎ 所以 所以，……………… 2分 所以四边形AMNF为平行四边形，…………3分 所以，……………… 4分 又因为平面,平面，‎ 所以平面．………………………5分 ‎（2）因为矩形平面，‎ 矩形平面， ‎ 所以平面．………………………………6分 如图，以B为原点建立空间直角坐标系，‎ 则，，，，………7分 因为轴平面ABCD，‎ 所以为平面ABCD的一个法向量，………………………………8分 设为平面AED的法向量，‎ 因为，，‎ 所以，得，‎ 故可取，………………………………11分 则，‎ 由图可知二面角的平面角为锐角，‎ 所以二面角的大小为．………………………………12分 理科数学答案与评分细则 第9页 共9页 解法二：‎ ‎(1)取CD中点F，分别连结FM,FN．‎ 又矩形ABCD中，M为AB中点，‎ 所以， ‎ 所以四边形AMFD为平行四边形， ‎ 所以，…………… 1分 又平面,平面，‎ 所以平面．………………… 2分 因为F、N分别为CD、CE的中点．‎ 所以， ‎ 又平面,平面，‎ 所以平面．……………… 3分 又因为，‎ 所以平面平面，………………4分 又平面，‎ 所以平面．………………………………5分 ‎(2)过点E作交CB的延长线于G，过G作交DA的延长线于H，连结EH，‎ 又因为平面平面，矩形平面 所以平面ABCD．‎ 又，‎ 平面，‎ 所以即为二面角的平面角，………………………………10分 因为,，‎ 所以，………………………………11分 由图可知二面角的平面角为锐角，‎ 所以二面角的大小为．……………………12分 理科数学答案与评分细则 第9页 共9页 ‎19．本小题主要考查正弦定理、余弦定理及三角恒等变换等基础知识，考查运算求解能力，考查化归与转化思想、函数与方程思想等，考查应用意识．满分12分．‎ 解：（1）解法—：因为，由正弦定理，得……………1分 又 所以…………………………………2分 所以，…………………………………3分 因为，所以 所以，又………………………………………4分 所以.……………………………………………………5分 ‎（2）由（1）知 ‎ 根据题意得 解得. ……………………………………………………6分 在中，由正弦定理得，‎ 所以………………………………………7分 因为，所以 所以……………………………………………………………8分 因为为中点，所以………………………………9分 所以 ‎………………………………10分 因为 所以的取值范围为………………………………12分 解法二：(1)因为，由余弦定理，得……………………1分 整理得 ………………………………2分 所以，………………………………4分 理科数学答案与评分细则 第9页 共9页 又，所以………………………………5分 ‎(2)由（1）知，又，故.…………………………6分 因为为锐角三角形，‎ 所以，即………………………7分 所以………………………………8分 延长到点，使得，连结，.‎ 则四边形为平行四边形，所以，.‎ 在中，，………………………………9分 即，所以，………………………………10分 因为，所以的取值范围为.………………………………12分 ‎20．本题主要考查直线、椭圆、直线与椭圆的位置关系等基础知识，考查运算求解能力、推理论证能力，考查函数与方程思想、化归与转化思想，考查考生分析问题和解决问题的能力，满分12分．‎ 解：（1）离心率为，，………………………………1分 的周长为8，，得，………………………………3分 ‎，，………………………………4分 因此，椭圆的标准方程为．………………………………5分 ‎（2）设的内切圆半径为，， ‎ 又，，‎ 要使的内切圆面积最大，只需的值最大．………………………………6分 设，，直线，‎ 联立消去得：，‎ 易得，且，，………………………………7分 理科数学答案与评分细则 第9页 共9页 所以 ‎，………………………………8分 设，则，………………………………9分 设，，所以在上单调递增，……………10分 所以当，即时，的最大值为3，………………………………11分 此时，所以的内切圆面积最大为．………………………………12分 ‎（注：若讨论直线斜率存在或不存在，由此求得斜率不存在时面积最大值，酌情按步给分）‎ ‎21．本题主要考查导数的几何意义、导数及其应用、不等式等基础知识，考查推理论证能力、运算求解能力、创新意识等，考查函数与方程思想、化归与转化思想、分类与整合思想、数形结合思想等．满分12分．‎ 解：（1）当时，，‎ ‎，………………………………1分 由，………………………………2分 得，‎ 即，……………………………3分 解得或.………………………………4分 当时，，此时直线恰为切线，故舍去，……………………5分 所以.………………………………6分 ‎（2）当时，，‎ 设，则，………………………………7分 故函数可化为.‎ 由,可得 的单调递减区间为，单调递增区间为，‎ 所以的最小值为，。………………………………8分 理科数学答案与评分细则 第9页 共9页 此时，函数的的值域为 问题转化为当时，有解，………………………………9分 即，得。‎ 设，则，‎ 故的单调递减区间为，单调递增区间为，‎ 所以的最小值为，………………………………11分 故的最小值为．………………………………………12分 ‎22．选修；坐标系与参数方程 本小题考查直线和圆的极坐标方程、参数方程等基础知识，考查运算求解能力，考查数形结合思想、化归与转化思想等． 满分10分．‎ 解法一：（1）圆的极坐标方程为，………………………………………1分 将代入得：‎ ‎，‎ 成立，‎ 设点对应的极径分别为，‎ 所以，………………………………………3分 所以，………………………………………4分 所以点轨迹的极坐标方程为，．………………………………………5分 ‎（2）由（1）得，……………………………6分 ‎，………………………………………7分 所以，，………………………………………8分 理科数学答案与评分细则 第9页 共9页 又，所以或，………………………………………9分 即或．………………………………………10分 解法二：‎ ‎（1）因为为中点，所以于，………………………………………1分 故的轨迹是以为直径的圆（在的内部），………………………………………2分 其所在圆方程为：，………………………………………3分 即.‎ 从而点轨迹的极坐标方程为，．………………………………………5分 ‎（2）由（1）得，………………………………6分 ‎，………………………………………7分 令，因为，所以， 则，‎ 所以，所以，………………………………………8分 即，解得（舍去），所以，‎ 又，，所以或，……………………………9分 即或． ………………………………10分 ‎23．选修：不等式选讲 本小题考查绝对值不等式的解法与性质等基础知识，考查运算求解能力、推理论证能力，考查分类与整合思想、化归与转化思想等． 满分10分．‎ ‎23．解：（1）构造，‎ 在上恒成立，，………………………………………1分 又，………………………………………3分 理科数学答案与评分细则 第9页 共9页 ‎，，………………………………………4分 的最大值．………………………………………5分 ‎（2）由（1）得，故．‎ ‎ ，，‎ 或．………………………………………6分 故．………………………………………7分 当时，，‎ ‎，‎ 当且仅当，即时取“=”；………………………………………8分 当时，，‎ ‎，‎ 当且仅当，即时取“=”．………………………………………9分 所以的取值范围是．………………………………………10分 理科数学答案与评分细则 第9页 共9页