高考理数　函数的图象 40页

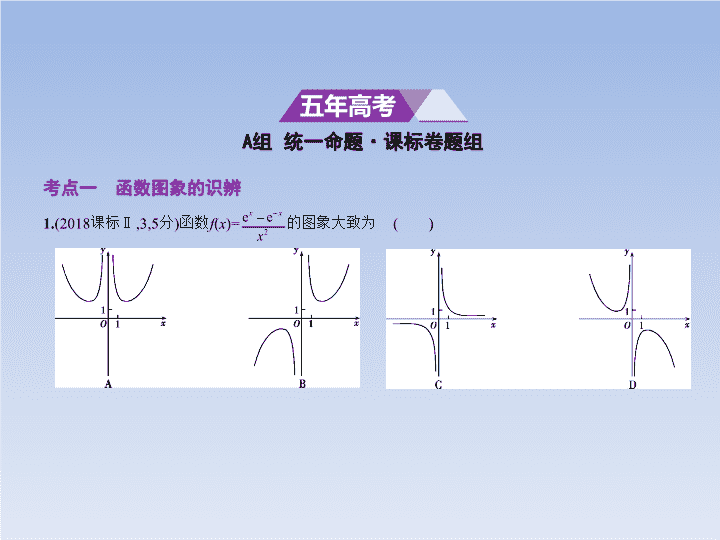
§2.5 　函数的图象 高考 理 数 ( 课标专用) A组  统一命题·课标卷题组 五年高考 考点一　函数图象的识辨 1. (2018课标Ⅱ,3,5分)函数 f ( x )=   的图象大致为   (　　) 答案      B 　本题主要考查函数的图象. 因为 f ( x )的定义域关于原点对称且 f (- x )=- f ( x ), 所以 f ( x )为奇函数,排除A选项; 由 f (2)=   >1,排除C、D选项.故选B. 方法总结 　函数图象的识辨方法 (1)由函数的定义域判断图象的左右位置,由函数的值域判断图象的上下位置; (2)由函数的单调性判断图象的变化趋势; (3)由函数的奇偶性判断图象的对称性; (4)由函数的周期性识辨图象; (5)由函数图象上的特征点排除不符合要求的图象. 2. (2018课标Ⅲ,7,5分)函数 y =- x 4 + x 2 +2的图象大致为   (　　)     答案      D 　本题考查函数图象的识辨. ∵ f ( x )=- x 4 + x 2 +2,∴ f '( x )=-4 x 3 +2 x ,令 f '( x )>0,解得 x <-   或0< x <   ,此时, f ( x )递增;令 f '( x )<0,解得-   < x <0或 x >   ,此时, f ( x )递减.由此可得 f ( x )的大致图象.故选D. 方法总结 　函数图象的识辨方法 函数图象识辨问题,通常是利用排除法解决.根据函数的定义域、值域、单调性、周期性、奇 偶性、对称性、特殊值等进行识辨. 3. (2016课标Ⅰ,7,5分)函数 y =2 x 2 -e | x | 在[-2,2]的图象大致为(　　) 答案      D 　令 f ( x )= y =2 x 2 -e | x | ,则 f (2)=8-e 2 >0,A错; f (2)=8-e 2 <1,B错,当 x >0时, f ( x )=2 x 2 -e x , f '( x )=4 x -e x , 当 x ∈   时, f '( x )<   × 4-e 0 =0,故 f ( x )在   上递减,C错.故选D. 思路分析 　先利用特值检验法排除A、B,再分析单调性排除C. 4. (2015课标Ⅱ,10,5分,0.439)如图,长方形 ABCD 的边 AB =2, BC =1, O 是 AB 的中点.点 P 沿着边 BC , CD 与 DA 运动,记∠ BOP = x .将动点 P 到 A , B 两点距离之和表示为 x 的函数 f ( x ),则 y = f ( x )的图象大致 为   (　　)          答案    B 　当点 P 与 C 、 D 重合时,易求得 PA + PB =1+   ;当点 P 为 DC 的中点时,有 OP ⊥ AB ,则 x =   ,易求得 PA + PB =2 PA =2   .显然1+   >2   ,故当 x =   时, f ( x )没有取到最大值,则C、D选项错 误.又当 x ∈   时, f ( x )=tan x +   ,不是一次函数,排除A,故选B. 思路分析 　求 P 位于特殊位置时 PA + PB 的值,分析选项中图象,利用排除法判断. 5. (2014课标Ⅰ,6,5分,0.682)如图,圆 O 的半径为1, A 是圆上的定点, P 是圆上的动点,角 x 的始边为 射线 OA ,终边为射线 OP ,过点 P 作直线 OA 的垂线,垂足为 M ,将点 M 到直线 OP 的距离表示成 x 的 函数 f ( x ),则 y = f ( x )在[0,π]上的图象大致为(　　)     答案    C 　由题图可知:当 x =   时, OP ⊥ OA ,此时 f ( x )=0,排除A、D;当 x ∈   时, OM =cos x ,设 点 M 到直线 OP 的距离为 d ,则   =sin x ,即 d = OM sin x =sin x cos x ,∴当 x ∈   时, f ( x )=sin x cos x =   sin 2 x ≤   ,排除B,故选C. 思路分析 　特殊值代入排除A,D   ,观察B、C的不同点   x ∈   时, f ( x ) max 与   的大小关系不同   ,利用函数 y = f ( x )在   上的最大值排除B. 考点二　函数图象的应用 (2016课标Ⅱ,12,5分)已知函数 f ( x )( x ∈R)满足 f (- x )=2- f ( x ),若函数 y =   与 y = f ( x )图象的交点为( x 1 , y 1 ),( x 2 , y 2 ), … ,( x m , y m ),则   ( x i + y i )=   (　　) A.0　    B. m 　    C.2 m 　    D.4 m 答案      B 　由 f (- x )=2- f ( x )可知 f ( x )的图象关于点(0,1)对称,又易知 y =   =1+   的图象关于点(0, 1)对称,所以两函数图象的交点成对出现,且每一对交点都关于点(0,1)对称,∴   ( x i + y i )=0 ×   +2 ×   = m .故选B. 思路分析 　分析出函数 y = f ( x )和 y =   的图象都关于点(0,1)对称,进而得两函数图象的交点成 对出现,且每一对交点都关于点(0,1)对称,从而得出结论. 考点一　函数图象的识辨 1. (2018浙江,5,4分)函数 y =2 | x | sin 2 x 的图象可能是   (　　)   B组  自主命题·省(区、市)卷题组 答案      D 　本小题考查函数的奇偶性,指数型函数、三角函数的值域. 因为 y =2 | x | sin 2 x 为奇函数,所以排除A,B;因为2 | x | >0,且当0< x <   时,sin 2 x >0,当   < x <π时,sin 2 x <0, 所以 x ∈   时, y >0, x ∈   时, y <0,所以排除C.故选D. 方法总结　 判断函数图象的方法 (1)利用函数的定义域、值域或函数在定义域的某个子区间上函数值的正负来判断; (2)利用函数的零点和零点个数来判断; (3)利用函数的奇偶性、单调性、周期性来判断; (4)利用函数图象的对称轴和对称中心来判断; (5)利用函数的极值和最值来判断; (6)利用函数图象上的特殊点(如函数图象与 x 轴、 y 轴的交点,图象上的最低点、最高点等)、 函数图象的渐近线来判断. 2. (2017浙江,7,5分)函数 y = f ( x )的导函数 y = f '( x )的图象如图所示,则函数 y = f ( x )的图象可能是   (　　)                   　       答案    D 　本题考查函数图象的识辨,利用导数判断函数的单调性和极值. 不妨设导函数 y = f '( x )的零点依次为 x 1 , x 2 , x 3 ,其中 x 1 <0< x 2 < x 3 ,由导函数图象可知, y = f ( x )在(- ∞ , x 1 )上 为减函数,在( x 1 , x 2 )上为增函数,在( x 2 , x 3 )上为减函数,在( x 3 ,+ ∞ )上为增函数,从而排除A,C. y = f ( x ) 在 x = x 1 , x = x 3 处取到极小值,在 x = x 2 处取到极大值,又 x 2 >0,排除B,故选D. 方法总结　 函数图象的识辨方法: 1. 利用函数图象上的特殊点 ( 如函数图象与 x 轴、 y 轴的交点 , 函数图象上的最高点、最低点等 ) 来识辨 . 2. 利用函数的定义域 , 在某个区间上的值域来识辨 . 3. 利用函数的单调性、极值 ( 常用导数来判断 ) 和函数的周期性来识辨 . 4. 利用函数的零点来识辨 . 5. 利用函数的奇偶性来识辨 , 若函数是奇 ( 或偶 ) 函数 , 则其图象关于原点 ( 或 y 轴 ) 对称 . 6. 利用函数图象的中心对称和轴对称来识辨 . 7. 利用函数图象的渐近线来识辨 . 如指数型函数、对数型函数、幂函数 ( 指数为负 ) 型函数 ( 含 反比例函数 ) 、正切型函数等 , 其图象都有渐近线 . 考点二　函数图象的应用 1. (2015北京,7,5分)如图,函数 f ( x )的图象为折线 ACB ,则不等式 f ( x ) ≥ log 2 ( x +1)的解集是   (　　)   A.{ x |-1< x ≤ 0}　    B.{ x |-1 ≤ x ≤ 1} C.{ x |-1< x ≤ 1}　    D.{ x |-1< x ≤ 2} 答案    C 　作出函数 y =log 2 ( x +1)的图象,如图所示:   其中函数 f ( x )与 y =log 2 ( x +1)的图象的交点为 D (1,1),结合图象可知 f ( x ) ≥ log 2 ( x +1)的解集为{ x |-1< x ≤ 1},故选C. 2. (2015安徽,9,5分)函数 f ( x )=   的图象如图所示,则下列结论成立的是   (　　)   A. a >0, b >0, c <0　    B. a <0, b >0, c >0 C. a <0, b >0, c <0　    D. a <0, b <0, c <0 答案    C 　函数 f ( x )的定义域为{ x | x ≠ - c },由题中图象可知- c = x P >0,即 c <0,排除B.令 f ( x )=0,可得 x =-   ,则 x N =-   ,又 x N >0,则   <0.所以 a , b 异号,排除A,D. 3. (2016山东,15,5分)已知函数 f ( x )=   其中 m >0.若存在实数 b ,使得关于 x 的方 程 f ( x )= b 有三个不同的根,则 m 的取值范围是 　　　     . 答案 　(3,+ ∞ ) 解析      f ( x )的大致图象如图所示,   要满足存在 b ∈R,使得方程 f ( x )= b 有三个不同的根,只需4 m - m 2 < m ,又 m >0,所以 m >3. C组    教师专用题组 考点一　函数图象的识辨 1.(2012课标,10,5分)已知函数 f ( x )=   ,则 y = f ( x )的图象大致为   (　　) 答案    B 　令 g ( x )=ln( x +1)- x ,则 g '( x )=   -1=   , ∴当-1< x <0时, g ' x )>0,当 x >0时, g '( x )<0,∴ g ( x ) max = g (0)=0. ∴ f ( x )<0,排除A、C,又由定义域可排除D,故选B. 评析     本题考查了函数的图象,考查了利用导数判断单调性,求值域,考查了数形结合的数学思想. 2. (2013山东,8,5分)函数 y = x cos x +sin x 的图象大致为(　　)   答案      D 　解法一:令 f ( x )= y = x cos x +sin x , ∵ f (- x )=- x ·cos x -sin x =- f ( x ),∴函数 y = x cos x +sin x 为奇函数,可排除B. 令 x cos x +sin x =0,得tan x =- x ,在同一坐标系中画出函数 y =tan x 和 y =- x 的图象如图,由图可知函数 y = x cos x +sin x 的零点有一个介于   到π之间,可排除A、C,故选D.   解法二:令 f ( x )= x cos x +sin x , 则 f (- x )=- x cos x -sin x =- f ( x ), ∴ f ( x )为奇函数, ∵奇函数的图象关于原点对称,而B中图象不关于原点对称,∴排除B; 当 x =   时, y =1,而由C中图象知当 x =   时, y ≠ 1, ∴排除C; 当 x =π时, y =-π,而A中,当 x =π时, y >0, ∴排除A,故选D . 考点二　函数图象的应用 1. (2013湖南,5,5分)函数 f ( x )=2ln x 的图象与函数 g ( x )= x 2 -4 x +5的图象的交点个数为   (　　) A.3　    B.2　    C.1　    D.0 答案    B 　在同一直角坐标系下画出函数 f ( x )=2ln x 与函数 g ( x )= x 2 -4 x +5=( x -2) 2 +1的图象,如图 所示.   ∵ f (2)=2ln 2> g (2)=1,∴ f ( x )与 g ( x )的图象的交点个数为2,故选B. 2. (2013安徽,8,5分)函数 y = f ( x )的图象如图所示,在区间[ a , b ]上可找到 n ( n ≥ 2)个不同的数 x 1 , x 2 , … , x n ,使得   =   = … =   ,则 n 的取值范围是   (　　)   A.{3,4}　    B.{2,3,4}　    C.{3,4,5}　    D.{2,3} 答案      B 　设   =   = … =   = k ,易知 y = f ( x )的图象与直线 y = kx 的交点的坐标满足上述 等式.又交点至少有两个,至多有四个,故 n 可取2,3,4. 考点一　函数图象的识辨 1.(2018山西吕梁一模,9)函数 y =e sin x (-π ≤ x ≤ π)的大致图象为(　　)   三年模拟 A组 201 6 —201 8 年 高考模拟·基础题 组 答案      D 　因为函数 y =e sin x (-π ≤ x ≤ π)为非奇非偶函数,所以排除A、C.函数的导数为 y '=e sin x ·cos x ,令 y '=0,得cos x =0,此时 x =   或 x =-   .当0< x <   时, y '>0,函数递增;当   < x <π时, y '<0,函数递减,所 以 x =   是函数 y =e sin x 的极大值点,所以选D. 2. (2018安徽淮北一模,8)函数 f ( x )=   +ln| x |的图象大致为   (　　)   答案      B 　当 x <0时,函数 f ( x )=   +ln(- x ),易知函数 f ( x )=   +ln(- x )在(- ∞ ,0)上递减,排除C,D;当 x >0 时,函数 f ( x )=   +ln x , f (2)=   +ln 2 ≠ 2,故排除A,选B. 3. (2017山西太原二模,7)函数 f ( x )=   的图象大致为   (　　)   答案    D 　函数 f ( x )=   的定义域为(- ∞ ,1) ∪ (1,+ ∞ ),且图象关于 x =1对称,排除B,C.取特殊 值,当 x =   时, f ( x )=2ln   <0,故选D. 4. (2017河南焦作二模,9)函数 f ( x )=| x |+   (其中 a ∈R)的图象不可能是   (　　)   答案      C 　当 a =0时,函数 f ( x )=| x |+   =| x |,函数的图象可以是B; 当 a =1时,函数 f ( x )=| x |+   =| x |+   ,函数的图象可以是A; 当 a =-1时,函数 f ( x )=| x |+   =| x |-   , x >0时,| x |-   =0只有一个实数根 x =1,函数的图象可以是D, 所以函数的图象不可能是C.故选C. 考点二　函数图象的应用 1. (2018湖南张家界二模,7)已知 f ( x )=   + x -   ,则 y = f ( x )的零点个数是   (　　) A.4　    B.3　    C.2　    D.1 答案      C      f ( x )=   ,令 f ( x )=0,可得2 | x | =- x 2 +3, 作出 y =2 | x | 与 y =- x 2 +3的函数图象如图所示:   由图象可知两函数图象有两个交点,故 f ( x )有2个零点.故选C. 2. (2018福建南平一模,12)已知函数 f ( x )( x ∈R)满足 f (- x )=4- f ( x ),若函数 y =   与 y = f ( x )图象的交 点为( x 1 , y 1 ),( x 2 , y 2 ), … ,( x 10 , y 10 ),则   =   (　　) A.10　    B.20　    C.-10　    D.-20 答案      D 　∵ f (- x )=4- f ( x ), ∴ f (- x )+ f ( x )=4,∴ f ( x )的图象关于点(0,2)对称,∵函数 y =   =2+   的 图象也关于点(0,2)对称,∴ x 1 + x 2 + x 3 + … + x 10 =0, y 1 + y 2 + y 3 + … + y 10 =5 × 4=20,则   =-20.故选D. 3. (2018河北保定一模,11)定义在R上的偶函数 f ( x )满足 f ( x +1)=- f ( x ),当 x ∈[0,1]时, f ( x )=-2 x +1,设 函数 g ( x )=   (-1 ≤ x ≤ 3),则函数 f ( x )与 g ( x )的图象所有交点的横坐标之和为   (　　) A.2　    B.4　    C.6　    D.8 答案      B 　∵ f ( x +1)=- f ( x ),∴ f ( x +2)=- f ( x +1)= f ( x ),∴ f ( x )的周期为2. 又 f ( x )为偶函数,∴ f (1- x )= f ( x -1)= f ( x +1),故 f ( x )的图象关于直线 x =1对称. 又 g ( x )=   (-1 ≤ x ≤ 3)的图象关于直线 x =1对称,作出 f ( x )和 g ( x )的图象如图所示:   由图象可知两函数图象在[-1,3]上共有4个交点,分别记从左到右各交点的横坐标为 x 1 , x 2 , x 3 , x 4 ,可 知 x = x 1 与 x = x 4 , x = x 2 与 x = x 3 分别关于 x =1对称,∴所有交点的横坐标之和为 x 1 + x 2 + x 3 + x 4 =1 × 2 × 2=4.故 选B. 4. (2018湖北荆州一模,11)设函数 f ( x )=3 x e x ,若存在唯一的整数 x 0 ,使得 f ( x 0 )< kx 0 - k ,则 k 的取值范围 是   (　　) A.   　    B.   C.   　    D.   ∪   答案    D      f ( x )=3 x e x ,令 y = kx - k ,∵ f '( x )=3e x ( x +1),∴ f ( x )=3 x e x 在(- ∞ ,-1]上是减函数,在(-1,+ ∞ )上是 增函数,又∵ y = kx - k 是恒过点(1,0)的直线,∴作 f ( x )=3 x e x 与 y = kx - k 的图象如图,当直线 y = kx - k 与 f ( x ) =3 x e x 的图象相切时,设切点为( x ,3 x e x ),则有   =3e x +3 x e x ,解得 x 1 =   , x 2 =   .令 g ( x )=3 x e x - kx + k . 结合图象可知:要满足题意,只需   或   解得   ≤ k <   或6e 2 < k ≤   .故选D.   5. (2016安徽江淮十校第一次联考,13)已知max{ a , b }表示 a , b 两数中的最大值.若 f ( x )=max{e | x | ,e | x -2| }, 则 f ( x )的最小值为 　　　     . 答案     e 解析 　在同一直角坐标系中,画出函数 y =e | x | , y =e | x -2| 的图象(图略),可知 f ( x )=max{e | x | ,e | x -2| }=   当 x ≥ 1时, f ( x ) ≥ e,且当 x =1时,取得最小值e; 当 x <1时, f ( x )>e. 故 f ( x )的最小值为 f (1)=e. 选择题(每题5分,共25分) 1. (2018湖南岳阳二模,8)已知函数 f ( x )=   则函数 y = f ( x )+3 x 的零点个数是   (　　) A.0　    B.1　    C.2　    D.3 B 组 201 6 —201 8 年 高考模拟·综合题组 (时间: 20 分钟　分值: 2 5分) 答案      C 　函数 y = f ( x )+3 x 的零点个数就是 y = f ( x )与 y =-3 x 两个函数图象的交点个数,如图所示,由函数的图象可知, 零点个数为2.故选C. 思路分析 　画出函数 y = f ( x )与 y =-3 x 的图象,判断函数图象的交点个数即可. 方法点拨 　函数零点问题可转化为相应函数图象交点问题,故可数形结合求解. 2. (2018河南濮阳二模,10)设 x 1 , x 2 , x 3 均为实数,且   =log 2 ( x 1 +1),   =log 3 x 2 ,   =log 2 x 3 ,则   (    　) A. x 1 < x 3 < x 2 　    B. x 3 < x 2 < x 1 C. x 3 < x 1 < x 2 　    D. x 2 < x 1 < x 3 答案      A 　画出函数 y =π - x , y =log 2 ( x +1), y =log 2 x , y =log 3 x 的图象,如图.   ∵   =log 2 ( x 1 +1),   =log 3 x 2 ,   =log 2 x 3 ,∴由图象可得 x 1 < x 3 < x 2 ,故选A. 思路分析　 在同一直角坐标系中画出函数 y =π - x , y =log 2 ( x +1), y =log 2 x , y =log 3 x 的图象,观察图象 即可得出结论. 3. (2018河南信阳二模,12)已知函数 f ( x )( x ∈R)满足 f (- x )=8- f (4+ x ),函数 g ( x )=   ,若函数 f ( x )与 g ( x )的图象共有168个交点,记作 P i ( x i , y i )( i =1,2, … ,168),则( x 1 + y 1 )+( x 2 + y 2 )+ … +( x 168 + y 168 )的值为   (    　) A.2 018　    B.2 017　    C.2 016　    D.1 008 答案      D 　函数 f ( x )( x ∈R)满足 f (- x )=8- f (4+ x ),可得 f (- x )+ f (4+ x )=8,即函数 f ( x )的图象关于点(2,4) 对称,由函数 g ( x )=   =   =4+   ,可知其图象关于点(2,4)对称,∵函数 f ( x )与 g ( x )的 图象共有168个交点,∴两图象在点(2,4)两边各有84个交点,且两边的点分别关于点(2,4)对称, 故得( x 1 + y 1 )+( x 2 + y 2 )+ … +( x 168 + y 168 )=(4+8) × 84=1 008.故选D. 解题关键　 由函数图象的对称性可知 f ( x )的图象关于(2,4)对称, g ( x )的图象也关于(2,4)对称,则 f ( x )与 g ( x )的图象的各交点分别关于(2,4)对称. 方法总结 　解此类求图象交点横、纵坐标之和的问题,常利用图象的对称性求解,即找出两图 象的公共对称轴或对称中心,从而得出各交点的公共对称轴或对称中心,由此得出定值求解. 4. (2017安徽“江南十校”3月联考,10)若函数 f ( x )的图象如图所示, 则 f ( x )的解析式可能是   (    　) A. f ( x )=   　    B. f ( x )=   C. f ( x )=   　    D. f ( x )=   答案    B 　由题中图象可知,函数的定义域为{ x | x ≠ a 且 x ≠ b }, f ( x )在(- ∞ , a )上为增函数,在( a ,0] 上先增后减,在[0, b )上为减函数,在( b ,+ ∞ )上先减后增. A项中 f ( x )的定义域为{ x | x ≠ -1且 x ≠ 1},此时 a =-1, b =1. f '( x )=   ,则 f '(-2)=   -   <0,与 f ( x )在(- ∞ ,-1)上递增不符. B项中 f ( x )的定义域为{ x | x ≠ ± 1}, f '( x )=   =   ,若 f '( x )>0,则 x <-1或-1< x <1-   或 x >1+   ,此时 f ( x )在各对应区间上为增函数,符合题意. 同理可检验C、D不符.故选B. 导师点睛 　利用性质排除A,利用导数求出增区间排除C、D. 5. (2017山东菏泽一模,10)设min{ m , n }表示 m 、 n 二者中较小的一个,已知函数 f ( x )= x 2 +8 x +14, g ( x ) =min     ,log 2 (4 x )   ( x >0),若 ∀ x 1 ∈[-5, a ]( a ≥ -4), ∃ x 2 ∈(0,+ ∞ ),使得 f ( x 1 )= g ( x 2 )成立,则 a 的最 大值为   (　　) A.-4　    B.-3　    C.-2　    D.0 答案      C 　令   =log 2 (4 x ),解得 x =1, 在同一直角坐标系中作出 y =   与 y =log 2 (4 x )的图象(图略),可知当0< x ≤ 1时,   ≥ log 2 (4 x ), 当 x >1时,   0)=   ∴当0< x ≤ 1时, g ( x )的值域为(- ∞ ,2], 当 x >1时, g ( x )的值域为(0,2), ∴ g ( x )的值域为(- ∞ ,2]. 易得 f ( x )=( x +4) 2 -2,其图象开口向上,对称轴为 x =-4,则当-4 ≤ a ≤ -3时,函数 f ( x )在[-5, a ]上的值域 为[-2,-1],显然满足题意; 当 a >-3时,函数 f ( x )在[-5, a ]上的值域为[-2, a 2 +8 a +14], 要满足 ∀ x 1 ∈[-5, a ]( a ≥ -4), ∃ x 2 ∈(0,+ ∞ ),使得 f ( x 1 )= g ( x 2 )成立, 只需 a 2 +8 a +14 ≤ 2,则-3< a ≤ - 2 , 综上所述,满足题意的 a 的取值范围为[-4,-2], ∴ a 的最大值为-2,故选C. 解题关键 　由 ∀ x 1 ∈[-5, a ]( a ≥ -4), ∃ x 2 ∈(0,+ ∞ ),使得 f ( x 1 )= g ( x 2 )成立,得 f ( x )在[-5, a ]上的值域是 g ( x )在(0,+ ∞ )上值域的子集是解题的关键.