江苏省苏锡常镇四市2020届高三第二次教学情况调研数学试题 Word版含解析 25页

- 1 - 江苏省 2019—2020 学年度苏锡常镇四市高三教学情况调研（二） 数学试题 第 I 卷（必做题，共 160 分） 一、填空题（本大题共 14 小题，每小题 5 分，共 70 分，请将答案填写在答题卷相应的位置 上.） 1.已知集合 A＝{1，2}，B＝{﹣1，a}，若 A  B＝{﹣1，a，2}，则 a＝_______. 【答案】1 【解析】 【分析】 根据集合 A B 中的元素，判断出 a 的值. 【详解】∵集合 A＝{1，2}，B＝{﹣1，a}，且 A  B＝{﹣1，a，2}， ∴a＝1. 故答案为：1 【点睛】本小题主要考查根据并集的结果求参数，属于基础题. 2.若复数 z 满足(1﹣i)z＝1＋i，其中 i 是虚数单位，则 z 的实部为_______. 【答案】0 【解析】 【分析】 利用复数的除法运算求得 z ，由此求得 z 的实部. 【详解】 2 2 2 1 (1 ) 1 2 1 (1 )(1 ) 1 i i i iz ii i i i           ，∴z 的实部为 0. 故答案为： 0 【点睛】本小题主要考查复数的除法运算，考查复数实部的概念，属于基础题. 3.某校 100 名学生参加知识竞赛的成绩均在[50，100]内，将学生成绩分成[50，60)，[60， 70)，[70，80)，[80，90)，[90，100]五组，得到如图所示的频率分布直方图，则成绩在[80， 90)内的学生人数是_______. - 2 - 【答案】30 【解析】 【分析】 用1减去成绩在 80,90 以外的学生的频率，将所得结果乘以100，求得成绩在 80,90 以内 的学生人数. 【详解】[1 (0.005 0.02 2 0.025) 10] 100 30       . 故答案为：30 【点睛】本小题主要考查根据频率分布直方图进行计算，属于基础题. 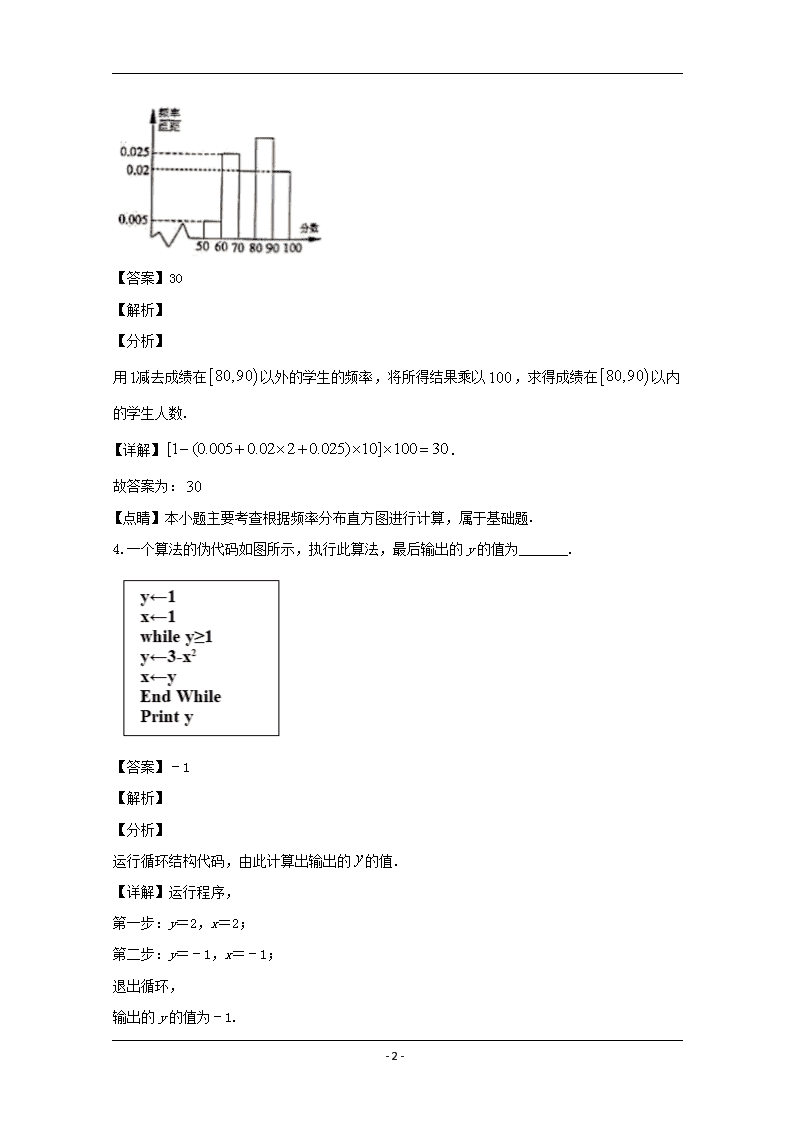4.一个算法的伪代码如图所示，执行此算法，最后输出的 y 的值为_______. 【答案】﹣1 【解析】 【分析】 运行循环结构代码，由此计算出输出的 y 的值. 【详解】运行程序， 第一步：y＝2，x＝2； 第二步：y＝﹣1，x＝﹣1； 退出循环， 输出的 y 的值为﹣1. - 3 - 故答案为： 1 【点睛】本小题主要考查根据循环结构程序代码计算输出结果，属于基础题. 5.某班推选一名学生管理班级防疫用品，已知每个学生当选是等可能的，若“选到女生”的 概率是“选到男生”的概率的 1 2 ，则这个班级的男生人数与女生人数的比值为_______. 【答案】2 【解析】 【分析】 根据“选到女生”的概率是“选到男生”的概率的 1 2 ，求得男生和女生人数的比值. 【详解】∵“选到女生”的概率是“选到男生”的概率的 1 2 ， ∴男生人数与女生人数的比值为 2. 故答案为： 2 【点睛】本小题主要考查概率的概念，属于基础题. 6.函数 2 lny x x   的定义域为_______. 【答案】 0,2 【解析】 【分析】 由函数 2 lny x x   有意义，得到 2 0 0 x x     ，即可求解，得到答案. 【详解】由题意，函数 2 lny x x   有意义，则满足 2 0 0 x x     ，解得 0 2x  ， 所以函数 2 lny x x   的定义域为 0,2 . 故答案为 0,2 . 【点睛】本题主要考查了函数的定义域的求解，其中解答中根据函数的解析式，得出函数解 析式有意义的不等式组是解答的关键，着重考查了推理与运算能力，属于基础题. 7.在平面直角坐标系xOy中，抛物线y2＝4x的焦点是双曲线 2 2 2 14 x y a a   的顶点，则a＝______. 【答案】1 - 4 - 【解析】 【分析】 先求得抛物线 2 4y x 的焦点坐标，根据抛物线的焦点是双曲线的顶点，求得 a 的值. 【详解】∵抛物线 y2＝4x的焦点是(1，0)， ∴双曲线 2 2 2 14 x y a a   的顶点为(1，0)，故 a＝1. 故答案为：1 【点睛】本小题主要考查抛物线的焦点、双曲线的顶点，属于基础题. 8.已知等比数列 na 的前 n 项和为 nS ， 4 25S S ， 2 2a  ，则 4a ＝_______. 【答案】2 或 8 【解析】 【分析】 根据已知条件进行化简，对 1 2a a 是否为零分成两种情况进行分类讨论，由此求得 4a 的值. 【详解】∵ na 为等比数列， 4 25S S ，∴ 1 2 3 4 1 25( )a a a a a a     ， ∴ 3 4 1 24( )a a a a   ， 当 1 2 0a a  时， 1q   ，此时 2 4 2 2a a q  ； 当 1 2 0a a  时， 2 4q  ，此时 2 4 2 2 4 8a a q    ， 综上所述， 4a ＝2 或 8. 故答案为： 2 或8 【点睛】本小题主要考查等比数列通项公式和前 n 项和公式的基本量计算，属于基础题. 9.已知正方体 ABCD—A1B1C1D1 的棱长为 6，点 M 是对角线 A1C 上靠近点 A1 的三等分点，则三棱 锥 C—MBD 的体积为_______. - 5 - 【答案】24 【解析】 【分析】 利用顶点转化的方法，由 =C MBD M BCDV V — 计算出几何体的体积. 【详解】 2 3 1 1 1 2 1= 6 243 2 3 9C MBD M BCDV V BC AA      — . 故答案为： 24 【点睛】本小题主要考查三棱锥体积的求法，属于基础题. 10.已知定义在 R 上的奇函数 ( )f x 的周期为 2，且 x[0，1]时， 12 , 0 2( ) 1 1,  11 2 x a x f x bx xx          ， 则 a＋b＝_______. 【答案】0 【解析】 【分析】 根据函数  f x 的奇偶性、周期性求得    1 , 0f f 的值，由此列方程，解方程求得 ,a b 的值， 进而求得 a b的值. 【详解】∵ ( )f x 为定义在 R 上的奇函数，∴ ( 1) (1)f f   ①， (0) 0f  ， ∵函数 ( )f x 的周期为 2，∴ ( 1) (1)f f  ②，由①，②得 ( 1) (1) 0f f   ∴ 0(0) 2 0 1 01 1(1) 02 f a a a bb bf               . - 6 - 故答案为： 0 【点睛】本小题主要考查函数的奇偶性和周期性，属于基础题. 11.已知锐角 满足sin 2 2cos2 1    ，则 tan( )4   ＝_______. 【答案】2 【解析】 【分析】 利用二倍角公式化简已知条件，并转化为只含 tan 的表达式，由此求得 tan 的值，进而求 得 tan 4     的值. 【详解】∵sin 2 2cos2 1    ， ∴ 2 2 2 22sin cos 2(cos sin ) sin cos 0          ， 化简得 2 23sin 2sin cos cos 0      ，两边同时除以 2cos  得， 23tan 2tan 1 0    ，∵ 为锐角，∴ tan ＞0 解得 1tan 3   ， ∴ 1 1tan tan 34tan( ) 214 1 tan tan 1 14 3           . 故答案为： 2 【点睛】本小题主要考查二倍角公式、同角三角函数的基本关系式，两角和的正切公式，属 于基础题. 12.如图，在△ABC 中，∠ABC＝ 2  ，AB＝1，BC＝3，以 AC 为一边在△ABC 的另一侧作正三角 形 ACD，则 BD AC  ＝_______. - 7 - 【答案】4 【解析】 【分析】 取 AC 的中点 E ，连接 ,ED BE ，则 ED AC .根据平面向量的线性运算以及数量积运算， 将 BD AC  转化为 2 21 ( )2 BC BA  ，由此求得 BD AC  的值. 【详解】取 AC 中点 E，连接 ,ED BE ，则 ED AC ，则 1( ) ( ) ( )2BD AC BE ED AC BE AC BA BC BC BA                    2 2 2 21 1( ) (3 1 ) 42 2BC BA       . 故答案为： 4 【点睛】本小题主要考查平面向量的线性运算、数量积运算，考查了化归与转化的数学思想 方法，属于基础题. 13.在平面直角坐标系 xOy 中，AB 是圆 O：x2＋y2＝1 的直径，且点 A 在第一象限；圆 O1：(x ﹣a)2＋y2＝r2(a＞0)与圆 O 外离，线段 AO1 与圆 O1 交于点 M，线段 BM 与圆 O 交于点 N，且 1 0OM O N    ，则 a 的取值范围为_______. 【答案】  2 2,4 【解析】 【分析】 根据 1 0OM O N    判断出四边形 1ONO M 为平行四边形，由此求得圆 1O 的方程以及 1AO 的 长，进而判断出 A 点在圆 2 2( ) 9x a y   上，根据圆 2 2( ) 9x a y   与圆 2 2 1x y  的位 - 8 - 置关系，求得 a 的取值范围. 【详解】 1 0OM O N     四边形 ONO1M 为平行四边形，即 ON＝MO1＝r＝1， 所以圆 1O 的方程为 2 2 1x a y   ， 且 ON 为△ABM 的中位线 AM＝2ON＝2 AO1＝3， 故点 A 在以 O1 为圆心，3 为半径的圆上，该圆的方程为： 2 2( ) 9x a y   ， 故 2 2( ) 9x a y   与 x2＋y2＝1 在第一象限有交点，即 2＜a＜4， 由  2 2 2 2 9 1 x a y x y       ，解得 2 8 0 2 22A ax aa     ， 故 a 的取值范围为( 2 2 ，4). 故答案为： 2 2,4 【点睛】本小题主要考查圆与圆的位置关系，考查化归与转化的数学思想方法，考查数形结 合的数学思想方法，属于难题. 14.已知 a，bR，a＋b＝t（t 为常数），且直线 y＝ax＋b 与曲线 exy x （e 是自然对数的底 数，e≈2.71828…）相切.若满足条件的有序实数对(a，b)唯一存在，则实数 t 的取值范围为 _______. - 9 - 【答案】  2 5, ee       【解析】 【分析】 设出切点坐标  0 0 0, exx x ，根据切点在切线和曲线上，以及导数与切线的斜率的关系列方程组， 由此求得 a b关于 0x 的表达式，构造函数  f x ，利用  'f x 研究  f x 的单调性，由此求 得t 的取值范围. 【详解】设切点为( 0x ， 0 0 xx e ) ( 1)e xy x   ， ∴ 0 0 0 20 0 0 0 ( 1)e e e x x x a x b x x ax b         ， 0 2 0 0e ( 1)xa b x x t      有唯一解， 构造函数  2( ) 1xf x e x x    ( ) e ( 2)( 1)xf x x x     ， x (  ，﹣2) ﹣2 (﹣2，1) 1 (1，  ) ( )f x ﹣ 0 ﹢ 0 ﹣ ( )f x 递减 2 5 e  递增 e 递减 注意到 2x   时   0f x  ， 故 ( )f x t 有唯一解时 t 的取值范围为(  ， 2 5 e  ) {e}. 故答案为：  2 5, ee       【点睛】本小题主要考查导数与切线问题，考查利用导数研究函数的单调性、极值，考查化 归与转化的数学思想方法，属于难题. - 10 - 二、解答题（本大题共 6 小题，共计 90 分，请在答题纸指定区域内作答，解答时应写出文字 说明、证明过程或演算步骤.） 15.已知△ABC 中，a，b，c 分别为角 A，B，C 的对边，且 bsin2A＝asinB. （1）求 A； （2）求 cos(B＋ 6  )＋sin(C＋ 3  )的最大值. 【答案】（1） 3  （2）1 【解析】 【分析】 （1）利用正弦定理和二倍角公式化简已知条件，由此求得 cos A，进而求得 A 的大小. （2）用 B 表示出C ，将所求表达式化为 sin( )3B  ，结合三角函数最值的求法，求得所求最 大值. 【详解】（1）∵bsin2A＝asinB，∴2bsinAcosA＝asinB， ∴由正弦定理 sin sin a b A B  ，得 2 cosba A ab ， ∵ 0ab  ，∴ 1cos 2A  ， 又∵三角形内角 A (0 ) ， ，∴A＝ 3  ； （2）由（1）A＝ 3  ，又 A＋B＋C＝ ，得 C＝ 2 3A B B     ，B 2(0 )3  ， ， cos(B＋ 6  )＋sin(C＋ 3  ) cos cos sin sin sin( )6 6B B B      1 3sin cos sin( )2 2 3B B B    ∵B 2(0 )3  ， ，∴ ( )3 3B     ， ，∴当 =3 2B   ， 即 6B  时， sin( )3B  取最大值 1， ∴cos(B＋ 6  )＋sin(C＋ 3  )的最大值为 1. 【点睛】本小题主要考查正弦定理解三角形，考查三角形内角和定理，考查三角函数最值的 求法，考查化归与转化的数学思想方法，属于中档题. 16.已知在四棱柱 ABCD—A1B1C1D1 中，底面 ABCD 是菱形，且平面 A1ADD1⊥平面 ABCD，DA1＝DD1， - 11 - 点 E，F 分别为线段 A1D1，BC 的中点. （1）求证：EF∥平面 CC1D1D； （2）求证：AC⊥平面 EBD. 【答案】（1）证明见解析；（2）证明见解析； 【解析】 【分析】 （1）连接 1CD ，通过证明四边形 1ED CF 是平行四边形，证得 1/ /EF CD ，由此证得 / /EF 平 面 1 1CC D D . （2）通过证明 DE AD ，结合面面垂直的性质定理证得 DE  平面 ABCD ，由此证得 DE AC ，由菱形的性质得到 BD AC ，从而证得 AC  平面 EBD . 【详解】（1）连结 CD1，四棱柱 ABCD—A1B1C1D1 中，A1B1C1D1，BB1C1C 是平行四边形， ∴A1D1//B1C1，BC//B1C1，且 A1D1＝B1C1，BC＝B1C1， 又∵点 E，F 分别为线段 AD，BC 的中点， ∴ED1//FC，ED1＝FC， 所以四边形 ED1CF 是平行四边形， ∴EF//CD1，又∵EF 平面 CC1D1D，CD 平面 CC1D1D， ∴EF//平面 CC1D1D. （2）四棱柱 ABCD—A1B1C1D1 中，四边形 AA1D1D 是平行四边形， ∴AD//A1D1，在△DA1D1 中，DA1＝DD1，点 E 为线段 A1D1 的中点， - 12 - ∴DE⊥A1D1，又∵AD//A1D1，∴DE⊥AD， 又∵平面 A1ADD1⊥平面 ABCD，平面 A1ADD1 平面 ABCD＝AD，DE 平面 A1ADD1， ∴DE⊥平面 ABCD，又 AC  平面 ABCD，∴DE⊥AC， ∵底面 ABCD 是菱形，∴BD⊥AC， 又∵BDDE＝D，BD，DE  平面 EBD， ∴AC⊥平面 EBD. 【点睛】本小题主要考查线面平行的证明，考查线面垂直的证明，考查空间想象能力和逻辑 推理能力，属于中档题. 17.在平面直角坐标系 xOy 中，椭圆 C： 2 2 2 2 1x y a b   (a＞b＞0)的离心率为 1 2 ，右焦点到右准 线的距离为 3. （1）求椭圆 C 的标准方程； （2）过点 P(0，1)的直线 l 与椭圆 C 交于两点 A，B.己知在椭圆 C 上存在点 Q，使得四边形 OAQB 是平行四边形，求 Q 的坐标. 【答案】（1） 2 2 14 3 x y  （2）Q(1， 3 2 )或(﹣1， 3 2 ) 【解析】 【分析】 （1）结合椭圆离心率以及右焦点到右准线的距离，以及 2 2 2b a c  ，求得 2 2, ,a b c ，进而求 得椭圆C 的标准方程. （2）首先判断直线l 斜率不存在时，四边形OAQB 不可能是平行四边形，不符合题意.然后 设出直线 l 的方程 1y kx  ，联立直线l 的方程和椭圆方程，写出根与系数关系，求得Q 点 坐标并代入椭圆方程，由此求得 k 的值，进而求得Q 点坐标. 【详解】（1）设焦距为 2c， ∵椭圆 C 的离心率为 1 2 ，∴ 1 2 c a  ①， ∵右焦点到右准线的距离为 3，∴ 2 3a cc   ②， 由①，②解得 a＝2，c＝1，故 b2＝a2﹣c2＝3， - 13 - ∴椭圆 C 的标准方程为 2 2 14 3 x y  ， （2）当直线 l 斜率不存在时，四边形 OAQB 不可能平行四边形，故直线 l 斜率存在 ∵直线 l 过点 P(0，1)，设直线 l 为： 1y kx  ， 设 A( 1x ， 1 1kx  )，B( 2x ， 2 1kx  )， 由四边形 OAQB 是平行四边形，得 Q( 1 2x x ， 1 2( ) 2k x x  ) 2 2 1 3 4 12 0 y kx x y       ，化简得： 2 2(3 4 ) 8 8 0k x kx    ， 1 2 2 2 1 2 2 8 8 3 4 82(3 4 ) 3 4 kx xk kx k x x k               ， 1 2 2 2 8 6( ) 2 ( ) 23 4 3 4 kk x x k k k         ， ∴Q( 2 8 3 4 k k   ， 2 6 3 4k )，∵点 Q 在椭圆 C 上， ∴ 2 2 2 2 8 63( ) 4( ) 123 4 3 4 k k k     ，解得 1 2k   ，代入 Q 的坐标，得 Q(1， 3 2 )或(﹣1， 3 2 ). 【点睛】本小题主要考查椭圆标准方程的求法，考查直线和椭圆的位置关系，考查运算求解 能力，属于中档题. 18.某地开发一片荒地，如图，荒地的边界是以 C 为圆心，半径为 1 千米的圆周.已有两条互 相垂直的道路 OE，OF，分别与荒地的边界有且仅有一个接触点 A，B.现规划修建一条新路（由 线段 MP， PQ ，线段 QN 三段组成），其中点 M，N 分别在 OE，OF 上，且使得 MP，QN 所在直线 分别与荒地的边界有且仅有一个接触点 P，Q， PQ 所对的圆心角为 6  .记∠PCA＝ 2 （道路宽 度均忽略不计）. - 14 - （1）若 5 12   ，求 QN 的长度； （2）求新路总长度的最小值. 【答案】（1）QN 的长度为 1 千米（2） 2 3+ 6  【解析】 【分析】 （1）连接 , ,CB CN CM ，通过切线的几何性质，证得四边形 BCQN 是正方形，由此求得QN 的长度. （2）用 表示出线段 MP ， PQ ，线段QN 的长，由此求得新路总长度的表达式，利用基本 不等式求得新路总长度的最小值. 【详解】（1）连接 CB，CN，CM，OM⊥ON，OM，ON，PM，QN 均与圆 C 相切 ∴CB⊥ON，CA⊥OM，CP⊥MP，CQ⊥NQ，∴CB⊥CA ∵∠PCA＝ 2 5 6  ，∠PCQ＝ 6  ，∴∠QCB＝ 52 6 6 2 2         ， 此时四边形 BCQN 是正方形，∴QN＝CQ＝1， 答：QN 的长度为 1 千米； - 15 - （2）∵∠PCA＝ 2 ，可得∠MCP＝ ，∠NCQ＝ 2 3   ， 则 MP＝ tan ， PQ 6  ，NQ＝ 2tan tan2 tan 33tan( ) 23 3 tan 11 tan tan3           设新路长为 ( )f  ，其中  ( 6  ， 2  )，即 3tan 3   ∴ tan 3 3 4 2 3( ) tan tan6 3 3 63 tan 1 3tan 3 f                  ， 3 4 2 32 tan 2 3+3 3 6 63tan 3               ，当 tan 3  时取“＝”， 答：新路总长度的最小值为 2 3+ 6  . 【点睛】本小题主要考查直线和圆的位置关系，考查三角函数在实际生活中的应用，考查基 本不等式求最值，考查化归与转化的数学思想方法，属于难题. 19.已知各项均为正数的数列 na 的前 n 项和为 nS ， 1 2a  ，且对任意 n N ， 1 1 12 2n n n n n na S a S a a     恒成立. （1）求证：数列 2n n S a       是等差数列，并求数列 na 的通项公式； （2）设 4 3n nb a n   ，已知 2b ， ib ， jb (2＜i＜j)成等差数列，求正整数 i，j. 【答案】（1）证明见解析； 2n na  （2）i＝4，j＝5 【解析】 【分析】 （1）根据题目所给递推关系式证得数列 2n n S a       是等差数列，由此得到 2 2n nS a  .利用 1 1 , 1 , 2n n n S na S S n     求得数列 na 的通项公式. （2）由（1）求得 nb 的表达式，由 2 , ,i jb b b 成等差数列列方程，分成 2j i  和 1j i  两种 情况进行分类讨论，由此求得整数 ,i j . - 16 - 【详解】（1）∵ 1 1 12 2n n n n n na S a S a a     ， ∴ 1 1( 2) ( 2)n n n na S a S    ， ∵数列 na 各项均为正数，∴ 1 0n na a   ，等式两边同时除以 1n na a  ， 得 1 1 2 2 0n n n n S S a a      ，故数列 2n n S a       是等差数列，首项为 2，公差为 0， ∴ 2 2n n S a   ，即 2 2n nS a  ①， 2 22 2S a  ，求得 2 4a  ， ∴ 1 12 2n nS a   (n≥2)②，①﹣②得 12 2n n na a a   ，即 12n na a  ， 又 2 14 2a a  ，∴对任意 n N ，数列 na 是以 2 为首项，2 为公比的等比数列 故数列 na 的通项公式为 2n na  ； （2） 4 3 2 4 3n n nb a n n      ， ∴ 2 9b  ， 2 4 3i ib i   ， 2 4 3j jb j   ， ∵ 2b ， ib ， jb (2＜i＜j)成等差数列， ∴ 2(2 4 3) 9 2 4 3i ji j      ， 变形得 1 1 1 2 3 2 12 2 j i i i i j        (*)， ①当 2j i  时， 1 12 1 12 j i i j     ， 令 1 2 3 2i i ic   (i≥3)，则 1 1 2 1 2 3 5 2 02 2 2i i i i i i i ic c         (i≥3)， ∴数列 ic 单调递减，故 (max) 3 3 14ic c   ， ∴ 1 2 3 12i i    ， 1 12 1 12 j i i j     ，故 2j i  时*式不成立， ②当 1j i  时，*式转化为 0 1 1 2 3 12 12 2i i i i       ，解得 i＝4，故 j＝5. 【点睛】本小题主要考查根据递推关系式求数列的通项公式，考查等差中项的性质，考查数 列的单调性，考查化归与转化的数学思想方法，考查分类讨论的数学思想方法，属于难题. 20.已知函数 ( ) ( 1) lnf x m x x   ， 2( ) ( 2) ( 3) 2g x m x n x     ，m，nR. （1）当 m＝0 时，求函数 ( )f x 的极值； - 17 - （2）当 n＝0 时，函数 ( ) ( ) ( )F x g x f x  在(0，  )上为单调函数，求 m 的取值范围； （3）当 n＞0 时，判断是否存在正数 m，使得函数 ( )f x 与 ( )g x 有相同的零点，并说明理由. 【答案】（1）函数 ( )f x 有极大值﹣1，无极小值;（2）m 的取值范围为{0};（3）存在正数 m， 使得函数 ( )f x 与 ( )g x 有相同的零点，详见解析. 【解析】 【分析】 （1）当 0m  时，利用  'f x 研究函数  f x 的单调性，由此求得函数  f x 的极值. （2）当 0n  时，由  ' 0F x  或  ' 0F x  恒成立，将 m 分成 0 2m  ， 0m  ， 2m  和 0m  四种情况进行分类讨论，由此求得 m 的取值范围. （3）设 0x 为相同的零点，由此得到 0 0 2 0 0 ( 1) ln 0 ( 2) ( 3) 2 0 m x x m x n x          ，进而得到 0 0 0 lnx xm x  ①， 2 0 0 0 0ln ( 3) 2 0x x x n x      ②.通过构造函数法，结合零点存在性定 理，证得①②能同时成立，由此证得存在符合题意的正数 m . 【详解】（1）当 m＝0 时， ( ) lnf x x x   ， ∴ 1( ) 1f x x     ，令 ( ) 0f x  ，解得 x＝1，列表如下： x (0，1) 1 (1，  ) ( )f x ＋ 0 － ( )f x 单调递增 单调递减 ∴当 x＝1 时，函数 ( )f x 有极大值﹣1，无极小值； （2）当 n＝0 时，函数 2( ) ( ) ( ) ( 2) ( 4) ln 2F x g x f x m x m x x        ∴ 22( 2) ( 4) 1 (2 1)[( 2) 1]( ) m x m x x m xF x x x          ， - 18 - 要使函数 ( ) ( ) ( )F x g x f x  在(0，  )上为单调函数， 则对 x (0，  )， ( ) 0F x ≥ 或 ( ) 0F x  恒成立， 令 ( ) (2 1)[( 2) 1]g x x m x    ， ( ) 0g x  或 ( ) 0g x  恒成立 ①当 0＜m＜2 时，x(0，1 2 ) ( 1 2 m ， )时， ( ) 0g x ，x( 1 2 ， 1 2 m )时， ( ) 0g x ， 不符题意； ②当 m＜0 时，x(0， 1 2 m ) ( 1 2 ， )时， ( ) 0g x ，x( 1 2 m ，1 2 )时， ( ) 0g x ， 不符题意； ③当 m≥2 时， x(0， 1 2 )时， ( ) 0g x ， x( 1 2 ，  )时， ( ) 0g x ，不符题意； ④当 m＝0 时， 2( ) (2 1) 0g x x    ，此时 ( ) 0F x  恒成立， 函数 ( ) ( ) ( )F x g x f x  在(0，  )上单调递减，符合题意， 综上所述，m 的取值范围为{0}； （3）∵函数 ( )f x 与 ( )g x 有相同的零点，不妨设 0x 为相同的零点 则 0 0 2 0 0 ( 1) ln 0 ( 2) ( 3) 2 0 m x x m x n x          ， 得 0 0 0 lnx xm x  ①， 2 0 0 0 0ln ( 3) 2 0x x x n x      ②， 由（1）知 ( ) ln (1) 1 0f x x x f       ，故 0 0ln 0x x  ， ∴ 0 0 0 ln 0x xm x   ， 令 2 0 0 0 0 0( ) ln ( 3) 2h x x x x n x      ， 又 (1) 0h n  ， ( +3) ( 3)ln( 3) 2 0h n n n      ， 故当 0x (1，n＋3)时， 0( ) 0h x  ，②式有解，且能满足 0 0 0 ln 0x xm x   ， ∴存在正数 m，使得函数 ( )f x 与 ( )g x 有相同的零点. - 19 - 【点睛】本小题主要考查利用导数研究函数的单调性和极值，考查函数零点问题的研究，考 查分类讨论的数学思想方法，考查化归与转化的数学思想方法，属于难题. 第 II 卷（附加题，共 40 分） 【选做题】本题包括 A，B，C 三小题，请选定其中两题作答，每小题 10 分共计 20 分，解答 时应写出文字说明，证明过程或演算步骤. 21.已知点 M(2，1)在矩阵 A＝ 1       2 a b      对应的变换作用下得到点 N(5，6)，求矩阵 A 的特征值. 【答案】矩阵 A 的特征值为 4 或﹣1 【解析】 【分析】 首先根据矩阵变换列方程组，解方程组求得 ,a b 的值，也即求得矩阵 A ，然后根据特征值的 求法，求得矩阵 A 的特征值. 【详解】∵点 M(2，1)在矩阵 A＝ 1       2 a b      对应的变换作用下得到点 N(5，6)， ∴ 1    2 5    2 1 6 a b                 ，则 2 5 2 2 6 a b      ，解得 3 2 a b    ，∴A＝ 1   3 2   2      ， 1     3( ) ( 1)( 2) 62       2f E A              ，令 ( ) 0f   ， 得 2 3 4 0    ，解得 1 4  ， 2 1   ， ∴矩阵 A 的特征值为 4 或﹣1. 【点睛】本小题主要考查矩阵特征值的求法，考查矩阵变换，属于基础题. 22.在平面直角坐标系 xOy 中，曲线 C 的参数方程为 2cos sin x y      ( 为参数).以原点 O 为极点， x 轴非负半轴为极轴建立极坐标系，直线 l 的极坐标方程为 sin( ) 104     . （1）求曲线 C 的普通方程和直线 l 的直角坐标方程； （2）点 P 是曲线 C 上的动点，求 P 到直线 l 的距离的最小值. 【答案】（1） 2 2 14 x y  ； 2 5 0x y   （2） 10 2 【解析】 - 20 - 【分析】 （1）利用 2 2sin cos 1   求得曲线C 的普通方程，由直角坐标和极坐标转化公式，求得 直线 l 的直角坐标方程. （2）设出 P 点的坐标，根据点到直线的距离公式，求得 P 到直线 l 的距离的表达式，根据三 角函数最值的求法，求得 P 到直线l 的距离的最小值. 【详解】（1）由题意，曲线 C 的普通方程为 2 2 14 x y  ， 由 sin( ) 104     得 2 2sin cos 102 2      ， 化简得直线 l 的普通方程为 2 5 0x y   . （2）设 P(2cos ，sin )，则 P 到直线 l 的距离 2cos sin 2 5 5 sin( ) 2 5 2 5 5 sin( ) 2 2 2 d              所以当sin( )  ＝1 时，dmin＝ 10 2 所以 P 到直线 l 的距离的最小值为 10 2 . 【点睛】本小题主要考查参数方程化为普通方程，考查极坐标方程转化为直角坐标方程，考 查利用参数求最值，属于中档题. 23.已知 a，b，c 是正数，求证：对任意 xR，不等式 2 1 b c ax x a b c       恒成立. 【答案】证明见解析； 【解析】 【分析】 先由基本不等式求得 b c a a b c   的最小值，然后根据绝对值三角不等式证得不等式成立. 【详解】对于正数 a，b，c，由均值不等式得 33 3b c a b c a a b c a b c       ， 当且仅当 a＝b＝c 时取“＝”， 任意 xR ，由绝对值不等式得 2 1 2 1 ( 2) ( 1) 3x x x x x x            - 21 - 当且仅当 x≤﹣1 时取“＝”， ∴对任意 xR ，都有不等式 2 1 b c ax x a b c       成立. 【点睛】本小题主要考查基本不等式和绝对值三角不等式，属于中档题. 【必做题】第 22 题、第 23 题，每题 10 分，共计 20 分，解答时应写出文字说明，证明过程 或演算步骤. 24.如图，在四棱锥 P—ABCD 中，底面 ABCD 是矩形，PA⊥平面 ABCD，AB＝2，AD＝AP＝3，点 M 是棱 PD 的中点. （1）求二面角 M—AC—D 的余弦值； （2）点 N 是棱 PC 上的点，已知直线 MN 与平面 ABCD 所成角的正弦值为 3 22 22 ，求 PN PC 的值. 【答案】（1） 2 17 17 （2） 1 4 PN PC  【解析】 【分析】 （1）建立空间直角坐标系，根据平面 ACD 和平面 MAC 的法向量，计算出二面角 M AC D  的余弦值. （2）设 ( (0,1))PN PC    ，由此求得 MN  ，根据直线 MN 与平面 ABCD 所成角的正弦 值列方程，解方程求得  的值，进而求得 PN PC . 【详解】（1）以{ AB  ， AD  ， AP  }为正交基底建立如图所示的空间直角坐标系 A—xyz， - 22 - 则各点的坐标为 A(0，0，0)，B(2，0，0)，C(2，3，0)，D(0，3，0)，P(0，0，3)，M(0， 3 2 ， 3 2 )， AP  ＝(0，0，3)， AC  ＝(2，3，0)， AM  ＝(0， 3 2 ， 3 2 ) 因为 PA⊥平面 ABCD，所以平面 ACD 的一个法向量为 AP  ＝(0，0，3)， 设平面 MAC 的法向量为 n  ＝(x，y，z)，所以 0 0 n AC n AM         ， 即 2 3 0 3 3 02 2 x y y z     ，取 n  ＝(3，﹣2，2)， ∴cos< AP  ， n  >＝ AP 6 2 17= = 173 9+4+4AP n n       ， ∴二面角 M—AC—D 的余弦值为 2 17 17 ； （2）设 ( (0,1))PN PC    ，其中 (2,3, 3)PC   ， ∴ 3 3 3 3(0, , ) (2 ,3 , 3 ) (2 ,3 , 3 )2 2 2 2MN MP PN                  ， ∵平面 ABCD 的一个法向量为 AP  ＝(0，0，3)， ∴ 2 2 2 33( 3 )2cos , 3 33 4 (3 ) ( 3 )2 2 AP MNAP MN AP MN                    - 23 - 2 33 2 922 18 2         ∵直线 MN 与平面 ABCD 所成角的正弦值为 3 22 22 ， ∴ 2 33 3 222 = 22922 18 2        ，∴ 2 2 3( 3 ) 92 =9 2222 18 2        ， 化简得 4 1  ，即 1 4   ，∴ 1 4 PN PC  . 【点睛】本小题主要考查面面角的求法，考查根据线面角求线段长度的比值，考查空间想象 能力，考查运算求解，属于中档题. 25.已知数列 na 中， 1 6a  ， 2 1 1 33n n na a a    (n N ). （1）分别比较下列每组中两数的大小：① 2a 和 36 2  ；② 3a 和 336 ( )2  ； （2）当 n≥3 时，证明： 2 2 3( ) 2( ) 36 2 n i ni i a    . 【答案】（1）① 2a ＝ 36 2  ；② 3a ＞ 336 ( )2  （2）证明见解析； 【解析】 【分析】 （1）根据递推关系式求得 2 3,a a ，比较出①②中两数的大小关系. （2）首先利用数学归纳法证明当 n≥3 时， ( 1) 236 ( )2 n n na    ，然后利用放缩法，证得所要证 明的不等式成立. 【详解】（1）①∵ 2 2 1 6 6 3 93a      ， 36 92   ，∴ 2a ＝ 36 2  ； ②∵ 2 3 1 9 9 3 213a      ， 33 816 ( )2 4   ，∴ 3a ＞ 336 ( )2  ； （2）先用数学归纳法证明：当 n≥3 时， ( 1) 236 ( )2 n n na    ， - 24 - 当 n＝3 时， 3a ＞ 336 ( )2  ； 假设当 n＝k（k≥3，k N ）时，结论成立，即 ( 1) 236 ( )2 k k ka    ， 当 n＝k＋1 时， ( 1) ( 1) 2 22 2 1 1 1 3 33 (6 ( ) ) 6 ( ) 33 3 2 2 k k k k k k ka a a            ( 1) ( 1) 22 21 3 3(6 ( ) ) 6 ( )3 2 2 k k k k      其中 ( 1) ( 1) 22 2 ( 3) 1 2 ( 1) ( 1) ( 1) 2 2 2 1 3 3(6 ( ) ) 6 ( ) 33 2 2 2( ) 123 3 36 ( ) 6 ( ) 6 ( )2 2 2 k k k k k k k k k k k k k a                 ， ∴ ( 1) 2 1 36 ( )2 k k ka     ，∴当 n＝k＋1 时，结论也成立， 综上所得，当 n≥3 时， ( 1) 236 ( )2 n n na    ， 从而，当 n≥3 时， 2 13( ) ( )6 2 nn na  ， 则 2 2 2 3 1 2 3 12 2 2 3 3 3 3 3 3 3( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( )6 6 2 2 2 2 2 2 2 n i n ni i a a                ， 131 ( )3 32 2( ) 332 21 2 n n       ， ∴当 n≥3 时， 2 2 3( ) 2( ) 36 2 n i ni i a    . 【点睛】本小题主要考查根据递推关系式求数列的项，考查数学归纳法证明不等式，考查放 缩法证明不等式，考查等比数列前 n 项和，属于难题. - 25 -