数学理卷·2017届山西省应县第一中学校高三10月月考（2017 9页

应 县 一 中 高 三 年 级 月 考 三 ‎ 数 学 试 题（理） 2016.10‎ 时间：120分钟 满分：150分 命题人：高冠军 一．选择题（共12题，每题5分）‎ ‎1.“红豆生南国,春来发几枝.愿君多采撷,此物最相思.”这是唐代诗人王维的《相思》诗,在这4句诗中,哪句可作为命题( )‎ A.红豆生南国 B.春来发几枝 C.愿君多采撷 D.此物最相思 ‎2.设全集U＝R，集合A＝{x|2x(x－2)＜1}，B＝{x|y＝ln (1－x)}，则图中阴影部分表示的集合为（ ）‎ A．{x|x≥1} B．{x|x≤1} ‎ C．{x|0＜x≤1} D．{x|1≤x＜2}‎ ‎3．设复数的共轭复数为，若（为虚数单位）则的值为( )‎ A. B. C. D.‎ ‎4.已知tanθ＝2，则sin2θ＋sinθcosθ－2cos2θ＝(　　)‎ A．－ B. C．－ D. ‎5．设f(n)＝＋＋…＋，n∈N＋，那么f(n＋1)－f(n)＝(　　)‎ A. B. C.＋ D.－ ‎6.设△ABC的三边长分别为a、b、c，△ABC的面积为S，内切圆半径为r，则r＝； ‎ 类比这个结论可知：四面体S－ABC的四个面的面积分别为S1、S2、S3、S4，内切球的半径为r，四面体S－ABC的体积为V，则r＝(　　)‎ A. B. C. D. 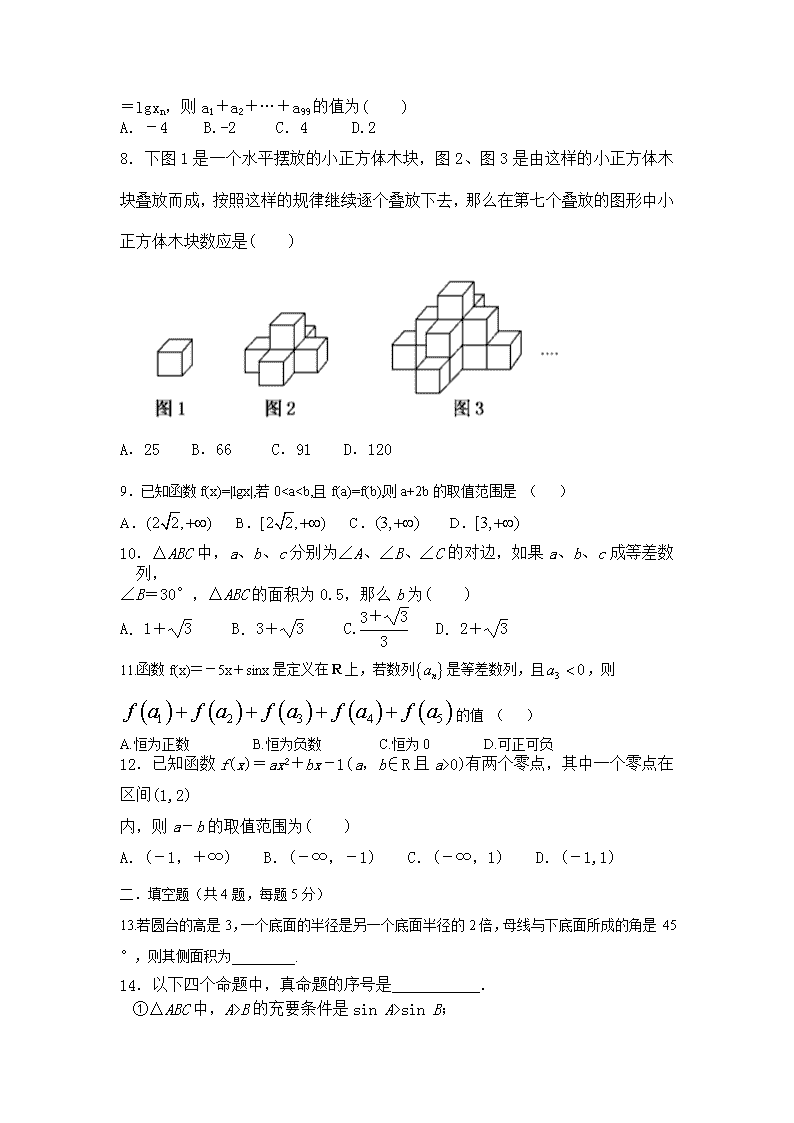‎7.设曲线y＝xn＋1(n∈N*)在点(1,1)处的切线与x轴的交点的横坐标为xn，令an＝lgxn，则a1＋a2＋…＋a99的值为(　　)‎ A．－4 B.-2 C．4 D.2‎ ‎8．下图1是一个水平摆放的小正方体木块，图2、图3是由这样的小正方体木块叠放而成，按照这样的规律继续逐个叠放下去，那么在第七个叠放的图形中小正方体木块数应是(　　)‎ A．25 B．66 C．91 D．120‎ ‎9．已知函数f(x)=|lgx|,若00)有两个零点，其中一个零点在区间(1,2)‎ 内，则a－b的取值范围为(　　)‎ A．(－1，＋∞) B．(－∞，－1) C．(－∞，1) D．(－1,1)‎ 二．填空题（共4题，每题5分）‎ ‎13.若圆台的高是3，一个底面的半径是另一个底面半径的2倍，母线与下底面所成的角是 45°，则其侧面积为_________.‎ ‎14．以下四个命题中，真命题的序号是___________．‎ ‎①△ABC中，A>B的充要条件是sin A>sin B；‎ ‎②函数y＝f(x)在区间(1,2)上存在零点的充要条件是f(1)·f(2)<0；‎ ‎③等比数列{an}中，a1＝1，a5＝16，则a3＝±4；‎ ‎④把函数y＝sin(2－2x)的图象向右平移2个单位后，得到的图象对应的解析式为 y＝sin(4－2x)． ‎ ‎15.（理）在正方体.中.M、N分别为棱与的中点，P为棱上的动点，则异面直线与NP所成的角为________．‎ ‎16.设M是△ABC内一点，且·＝2，∠BAC＝30°，定义f(M)＝(m，n，p)，其中m，n，p分别是△MBC，△MCA，△MAB的面积．若f(M)＝，则＋的最小值是________．‎ 三．解答题（共6题，第17题为10分，其余各题每题为12分）‎ ‎17. （本题满分10分）‎ ‎ ‎ ‎18．（本题满分12分）‎ ‎ 已知数列是首项为，公比的等比数列，设 ‎ ‎ ，数列.‎ ‎（1）求数列的通项公式；（2）求数列的前n项和Sn.‎ ‎19．（本题满分12分）‎ ‎ 已知向量＝(sinA，)与＝(3，sinA＋cosA)共线，其中A 是△ABC的内角．‎ ‎(1)求角A的大小；‎ ‎(2)若BC＝2，求△ABC的面积S的最大值，并判断S取得最大值时△ABC的形状．‎ ‎20．（本题满分12分）‎ ‎ 已知数列的前项和为，若且．‎ ‎(Ⅰ)求证是等差数列，并求出的表达式；‎ ‎(Ⅱ) 若，求证．‎ ‎21.（本题满分12分）设＝，‎ ‎＝(4sin x，cos x－sin x)，f(x)＝·‎ ‎(1)求函数f(x)的解析式；‎ ‎(2)已知常数ω>0，若y＝f(ωx)在区间上是增函数，求ω的取值范围；‎ ‎(3)设集合A＝，B＝{x||f(x)－m|<2}，若A⊆B，求实数m的取值范围．‎ ‎22. （本题满分12分）已知函数.‎ ‎（1）当时，求的极值； （2）求的单调区间；‎ ‎（3）若对任意的，恒有 成立，求实数的取值范围.‎ 高三数学月考三答案2016.10 ‎ ‎1.解析:因为命题是能判断真假的语句,它必须是陈述句,所以首先我们要凭借语文知识判断这4句诗哪句是陈述句,然后再看能否判定其真假.‎ ‎“红豆生南国”是陈述,意思是“红豆生长在中国南方”,这在唐代是事实,故本语句是命题;“春来发几枝”中的“几”是概数,无法判断其真假,故不是命题;‎ ‎“愿君多采撷”是祈使句,所以不是命题;“此物最相思”是感叹句,故不是命题.答案:A ‎2.解析　由2x(x－2)＜1得x(x－2)＜0，‎ 故集合A＝{x|0＜x＜2}，由1－x＞0得x＜1，故B＝{x|x＜1}，‎ 所以A∩B＝{x|0＜x＜1}，所以∁A(A∩B)＝{x|1≤x＜2}，‎ 即图中阴影部分表示的集合为{x|1≤x＜2}．答案　D 3.D ‎4.解析：sin2θ＋sinθcosθ－2cos2θ ‎＝＝＝＝.答案：D ‎5.【解析】　f(n＋1)－f(n)＝＋＋…＋＋－－－…－＝＋－＝－.【答案】　D ‎6.解析：设三棱锥的内切球球心为O，那么由V＝VO－ABC＋VO－SAB＋VO－SAC＋VO－SBC，‎ 即：V＝S1r＋S2r＋S3r＋S4r，可得：r＝.答案：C ‎7.[答案]　－2 [解析]　本小题主要考查导数的几何意义和对数函数的有关性质．‎ k＝y′|x＝1＝n＋1，∴切线l：y－1＝(n＋1)(x－1)，‎ 令y＝0，x＝，∴an＝lg，∴原式＝lg＋lg＋…＋lg＝lg××…×＝lg＝－2. B ‎8.分析：求解此题，如果按照前三个图所示的规律继续叠放，叠放至第七个图形后再去数图中小正方体木块数，自然也可以得出结论，但显然是太麻烦了，故还是应采取归纳推理的方法求解．‎ 解析：图1是1个小正方体木块，图2是2＋1×4个小正方体木块，图3是3＋(1＋2)×4个小正方体木块，按照前三个图所反映出来的规律，归纳推理可知，第七个叠放的图形中小正方体的木块数应是7＋(1＋2＋3＋…＋6)×4＝91.选C.答案：C ‎9.C 【命题意图】本小题主要考查对数函数的性质、函数的单调性、函数的值域， 考生在做本小题时极易忽视a的取值范围，而利用均值不等式求得a+2b,从而错选A,这也 是命题者的良苦用心之处.‎ ‎【解析】因为 f(a)=f(b),所以|lga|=|lgb|,所以a=b(舍去)，或，所以a+2b=‎ 又0f(1)=1+=3,即a+2b的取值范围是(3,+∞).‎ ‎10.解析：2b＝a＋c，ac·＝⇒ac＝2，a2＋c2＝4b2－4，b2＝a2＋c2－2ac·⇒b2＝⇒b＝.答案：C ‎ ‎11.【答案】A ‎ ‎12.解析：依题意得f(1)f(2)<0⇔(a＋b－1)(4a＋2b－1)<0，‎ 即或(不合题意，舍去)，满足不等式组的区域如图阴影部分所示(不包括边界)．‎ 令z＝a－b，即b＝a－z.当它经过两直线的交点A(0,1)时，－z取得最大值，即－zmax＝1，即z≥－1.又不等式组的区域不包括边界，所以z>－1.也就是a－b>－1，故选A.答案：A ‎13. 14① 15文① 15.理 ‎ ‎16.[答案]18 [解析]　∵·＝||·||cos30°＝|AB|·|AC|＝2，∴|AB|·|AC|＝4，由f(M)的定义知，S△ABC＝＋x＋y，又S△ABC＝|AB|·|AC|·sin30°＝1，∴x＋y＝(x>0，y>0)∴＋＝2(x＋y)＝2≥2(5＋2)＝18，等号在＝，即y＝2x＝时成立，∴min＝18.‎ ‎17. 解析：（1）α、β为根，a为系数，可以用韦达定理这座“桥”实现两者之间的互化，注意将根写成和与积的形式。‎ 解: ……………2分 ‎ ‎ ‎ ‎ ‎ ……………5分 ‎ ‎ ‎ ‎ ‎ ……………10分 ‎18.【解】（1）由题意知， ，……………2分 又，故 ……………4分 ‎（2）由（1）知，5分……7分 于是8分 两式相减，得 ‎10分 ‎……………12分 ‎19.解：(1)因为m∥n，所以sinA·(sinA＋cosA)－＝0. ……………2分 所以＋sin2A－＝0，即sin2A－cos2A＝1，‎ 即sin(2A－)＝1. ……………4分 因为A∈(0，π)，所以2A－∈(－，)．故2A－＝，A＝. ……………6分 设角A、B、C所对的边分别为a，b，c，则由余弦定理，得4＝b2＋c2－bc. ………7分 而b2＋c2≥2bc，∴bc＋4≥2bc，∴bc≤4(当且仅当b＝c时等号成立)， …………9分 所以S△ABC＝bcsinA＝bc≤×4＝. ……………10分 当△ABC的面积取最大值时，b＝c.又A＝，故此时△ABC为等边三角形．………12分 ‎20.【解】（I）证明：∵‎ ‎∴当n≥2时，an = Sn – Sn – 1 ……………1分 又 ‎∴， ……………2分 ‎ 若Sn = 0，则an = 0，∴a1 = 0与a1 =矛盾！∴Sn≠0，Sn – 1≠0． ‎ ‎∴即 ……………3分 又． ∴{}是首项为2，公差为2的等差数列 ………4分 ‎∵数列{}是等差数列．‎ ‎∴即 ……………5分 ‎∴当 ……………6分 又当 ‎∴ ……………7分 ‎（II）证明：由（II）知 ……………8分 ‎∴‎ ‎ ……………10分 ‎ ……………12分 ‎21.解　(1)f(x)＝sin2·4sin x＋(cos x＋sin x)·(cos x－sin x)‎ ‎＝4sin x·＋cos 2x＝2sin x(1＋sin x)＋1－2sin2x＝2sin x＋1，‎ ‎∴f(x)＝2sin x＋1. ……………4分 ‎(2)∵f(ωx)＝2sin ωx＋1，ω>0.由2kπ－≤ωx≤2kπ＋，‎ 得f(ωx)的增区间是，k∈Z. ……………6分 ‎∵f(ωx)在上是增函数，∴⊆. ……………7分 ‎∴－≥－且≤，∴ω∈. ……………-8分 ‎(3)由|f(x)－m|<2，得－2