数学（理）卷·2017届福建省长泰一中高三上学期期中考试（2016 4页

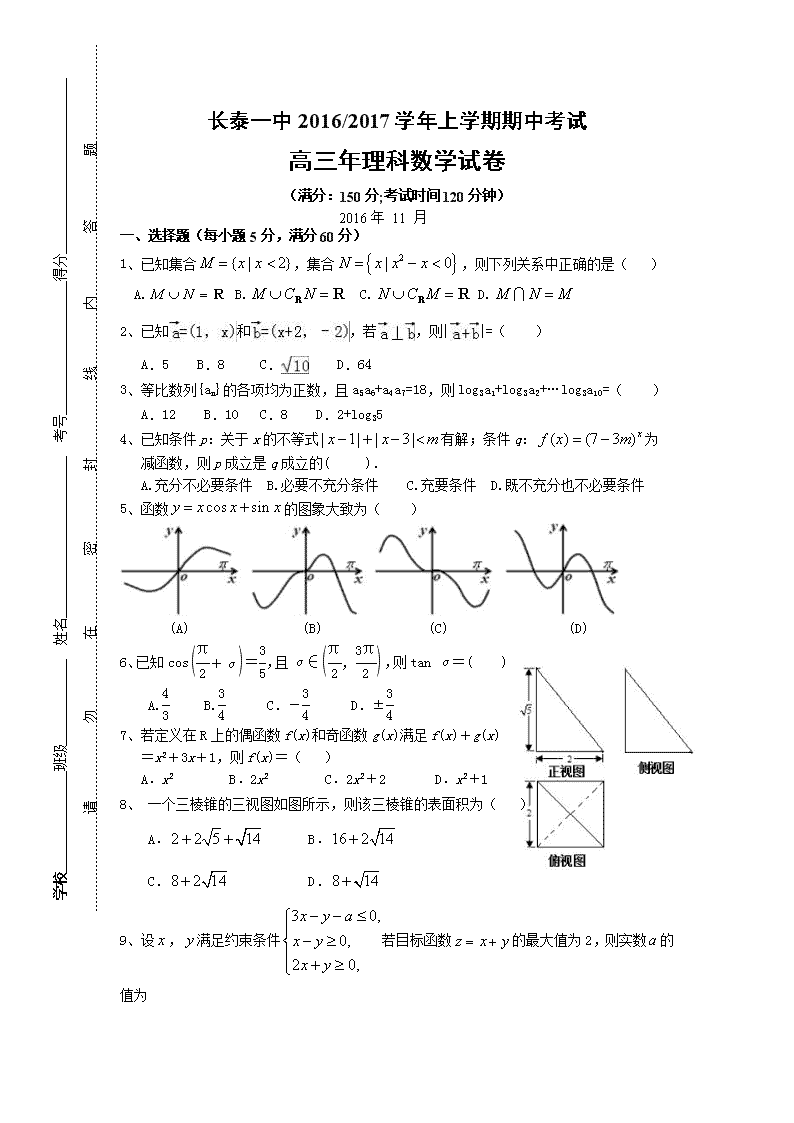
学校 　 　　　班级 姓名 　 考号 得分 　　　　　　　　‎ ‎ 请 　　 勿 　　 在 　　 密 　　 封 　 线 　　内 　 答 题 ‎ 长泰一中2016/2017学年上学期期中考试 高三年理科数学试卷 ‎（满分：150分;考试时间120分钟）‎ ‎2016年 11 月 一、选择题（每小题5分，满分60分）‎ ‎1、已知集合，集合，则下列关系中正确的是（ ）‎ ‎ A. B. C. D.‎ ‎2、已知和，若，则||=（　　）‎ ‎ A．5 B．‎8 ‎ C． D．64‎ ‎3、等比数列{an}的各项均为正数，且a‎5a6+a‎4a7=18，则log‎3a1+log‎3a2+…log‎3a10=（　　）‎ ‎ A．12 B．‎10 ‎C．8 D．2+log35‎ 4、 已知条件p：关于x的不等式有解；条件q：为 ‎ 减函数，则p成立是q成立的( )．‎ A.充分不必要条件 B.必要不充分条件 C.充要条件 D.既不充分也不必要条件 ‎5、函数的图象大致为（ ）‎ ‎(A)  (B) (C)  (D) ‎ ‎6、已知cos＝，且α∈，则tan α＝(　　)‎ A. B. C．－ D．± ‎7、若定义在R上的偶函数f(x)和奇函数g(x)满足f(x)＋g(x)‎ ‎ ＝x2＋3x＋1，则f(x)＝（ ）‎ ‎ A．x2 　　　B．2x‎2 ‎ 　　　C．2x2＋2 　　　D．x2＋1 ‎ ‎8、 一个三棱锥的三视图如图所示，则该三棱锥的表面积为（ ）‎ ‎ A． B． ‎ ‎ C． D．‎ 9、 设，满足约束条件若目标函数的最大值为2，则实数的值为 ‎ （ ） A． B．‎1 C． D．‎ ‎10、三棱锥中，平面，，，则三棱锥 ‎ ‎ 外接球的体积是（ ）‎ ‎ A． B． C． D．‎ 11、 已知等差数列的公差，且，，成等比数列，若，为数列的 ‎ ‎ 前项和，则的最小值为（ ）‎ ‎ A．4 B．‎3 ‎C． D．2‎ ‎12、已知函数满足：，那么下列不等式成立的是（ ）‎ ‎ (A) (B) (C)  (D) ‎ 二、填空题（每小题5分，共20分）‎ ‎13．在△ABC中，∠A＝60°，AB＝2，且△ABC的面积为，则BC的长为_______．‎ ‎14．若幂函数f（x）过点（2，8），则满足不等式f（2﹣a）＞f（1﹣a）的实数a的取值 ‎ 范围是　 　．‎ ‎15.若,则的最小值是 ．‎ ‎16.设函数的图象上存在两点，，使得△是以为直角顶点的 ‎ 直角三角形（其中为坐标原点），且斜边的中点恰好在轴上，则实数的取值范围 ‎ 是 ．‎ 三、解答题（前五大题每题12分，选做题10分，共70分）‎ ‎17. (本小题满分12分)在△ABC中，内角A，B，C所对的边分别为a，b，c.‎ ‎ 已知tan＝2.‎ ‎(1)求的值；‎ ‎(2)若B＝，a＝3，求△ABC的面积． ‎ ‎18.(本小题满分12分)数列的前项和为，且，设，．‎ ‎ （1）求数列的通项公式；‎ ‎ （2）求数列的前项和 19． ‎(本小题满分12分)在△ABC中，内角A，B，C的对边分别为a，b，c，已知 ‎ ， 且，‎ ‎ （Ⅰ）求△ABC的面积．‎ ‎ （Ⅱ）已知等差数列{an}的公差不为零，若a1cosA=1，且a2，a4，a8成等比数列，‎ ‎ 求{}的前n项和Sn．‎ 20. ‎(本小题满分12分) 如图，在四棱锥中，‎ 平面平面， ， ，‎ ‎，，，.‎ ‎ （1）求证：平面； ‎ ‎ （2）求直线与平面所成角的正弦值；‎ ‎（3）在棱上是否存在点，使得平面 ‎ ？若存在，求的值；若不存在，说明理由.‎ ‎21．（本小题满分12分）已知函数，函数，其中． ‎ ‎（1）如果函数与在处的切线均为，求切线的方程及的值；‎ ‎（2）如果曲线与有且仅有一个公共点，求的取值范围．‎ ‎ ‎ ‎ 请考生在第22-23题中任选一题作答，如果多做，则按所做的第一题计分.‎ ‎ 22．(本小题满分10分)在平面直角坐标系中，椭圆C的参数方程为（θ为参数）， ‎ ‎ 已知以坐标原点为极点，x轴的正半轴为极轴建立极坐标系，射线l的极坐标方程为θ=α ‎ （ρ≥0）（注：本题限定：ρ≥0，θ∈[0，2π））‎ ‎ （1）把椭圆C的参数方程化为极坐标方程；‎ ‎ （2）设射线l与椭圆C相交于点A，然后再把射线l逆时针90°，得到射线OB与 ‎ 椭圆C相交于点B，试确定是否为定值，若为定值求出此定值，若不为 ‎ 定值请说明理由．‎ ‎23．(本小题满分10分)设函数f（x）=|x﹣a|．‎ ‎ （1）当a=2时，解不等式f（x）≥7﹣|x﹣1|；‎ ‎ （2）若f（x）≤1的解集为[0，2]， +=a（m＞0，n＞0），求证：m+4n≥2+3．‎ 附加题（本题不计入总分）‎ ‎24．已知函数g（x）=（2﹣a）lnx，h（x）=lnx+ax2（a∈R），令f（x）=g（x）+h′（x），其中h′（x）是函数h（x）的导函数．‎ ‎（Ⅰ）当a=0时，求f（x）的极值；‎ ‎（Ⅱ）当﹣8＜a＜﹣2时，若存在x1，x2∈[1，3]，使得恒成立，求m的取值范围