江西省赣县三中2018-2019学年高二12月月考数学（文）试卷 Word版缺答案 4页

赣县第三中学高二年级2018-2019学年第一学期 ‎12月考数学（文科）试题 出题人：张小华 审题人：温文仁 时间：2018.12‎ 一．选择题。（本题共12小题，每小题5分，共60分。每个小题只有一个正确选项。）‎ ‎1、从甲乙两个城市分别随机抽取16台自动售货机，对其销售额进行统计，统计数据用茎叶图表示(如图所示)，设甲乙两组数据的平均数分别为X甲，X乙，中位数分别为m甲，m乙则（ ）‎ A． x甲＜x乙，m甲＞m乙 B． x甲＞x乙，m甲＞m乙 C． x甲＞x乙，m甲＜m乙 D． x甲＜x乙，m甲＜m乙 ‎2．某单位为了解用电量y（单位：度）与气温x（单位：℃）之间的关系，随机统计了某4天的用电量与当天的气温，并制作了如下对照表：‎ 气温x（℃）‎ ‎18‎ ‎13‎ ‎10‎ 用电量y（度）‎ ‎24‎ ‎34‎ ‎38‎ ‎64‎ 由表中数据得到回归直线方程y=-2x+a，预测当气温为-4℃时，用电量为（ ）‎ A． 68.2度 B． 68度 C． 69度 D． 67度 ‎3、从集合{2,3,4,5}中随机抽取一个数a,从集合{1,3,5}中随机抽取一个数b,则向量m=(a,b)与向量n=(1,-1)垂直的概率为(　　)‎ A． B． C． D． ‎ ‎4、在下列四个命题中：‎ ‎①命题“x>0，总有(x+1)ex>1”的否定是“x00 ,使得(x0+1)ex0 ”；‎ ‎②把函数y=3sin(2x+)的图象向右平移得到y=3sin2x的图象；‎ ‎③甲、乙两套设备生产的同类型产品共4800件，采用分层抽样的方法从中抽取一个容量为80的样本进行质量检测若样本中有50件产品由甲设备生产，则乙设备生产的产品总数为1800件；‎ ‎④“a+b=2”是“直线x+y=0与圆相切”的必要不充分条件 错误的个数是（ ）‎ A． 0 B． 1 C． 2 D． 3‎ ‎5、定义运算为执行如图所示的程序框图输出的S值，则式子的值是（ ）‎ A． ‎－1 B． C． 1 D． ‎ ‎6.从装有5个红球和3个白球的口袋内任取3个球，那么互斥而不对立的事件是（ ）‎ A. 至少有一个红球与都是红球 ‎ B. 至少有一个红球与都是白球 C. 恰有一个红球与恰有二个红球 ‎ D. 至少有一个红球与至少有一个白球 ‎7．在区间 [-,]上随机取一个数x，cos x的值介于0到之间的概率为( ).‎ A． B． C． D． ‎ ‎8、A，B，C，D四点都在一个球面上，AB=AC=AD=，且AB，AC，AD两两垂直，则该球的表面积为（　　）‎ A．6π B． C．12π D．‎ ‎9、如图所示，网格纸上小正方形的边长为1，粗实线和虚线画出的是某几何体的三视图，则该几何休的表面积为（ ）‎ A. B. ‎ C. D. ‎ ‎10、已知集合A=,集合B=,若A,则实数r可以取的一个值是（ ）‎ A． B． C．2 D．1+ ‎ ‎11．著名数学家华罗庚曾说过：“数形结合百般好，隔裂分家万事休．”事实上，有很多代数问题可以转化为几何问题加以解决，如：可以转化为平面上点M(x，y)与点N(a，b)的距离．结合上述观点，可得f(x)=的最小值为(　　)‎ A． B． C． 4 D． 8‎ ‎12、已知矩形ABCD，AB=2，BC=x，将沿矩形的对角线BD所在的直线进行翻折，在翻折过程中，则（ ）．‎ A． 当x=1时，存在某个位置，使得 B． 当时，存在某个位置，使得 C． 当x=4时，存在某个位置，使得 D． 时，都不存在某个位置，使得 二、填空题(每小题5分，共20分)‎ ‎13.设椭圆的长轴长、短轴长、焦距成等差数列,则b值为_________ ‎ ‎14.设p:<0，q：0b>0)的右焦点为F，过F作y轴的平行线交椭圆于M、N两点，若|MN|＝3，且椭圆离心率是方程2x2－5x＋2＝0的根，求椭圆方程．‎ ‎18.已知设成立；指数函数为增函数，如果“p或q”为真，“p且q”为假，求实数的取值范围.‎ ‎19、如图，四棱锥P-ABCD中，底面ABCD是边长为2的正方形，PB，且PA=2，E为PD中点.‎ ‎（1）求证：PA；（2）求几何体P-ABE的体积.‎ ‎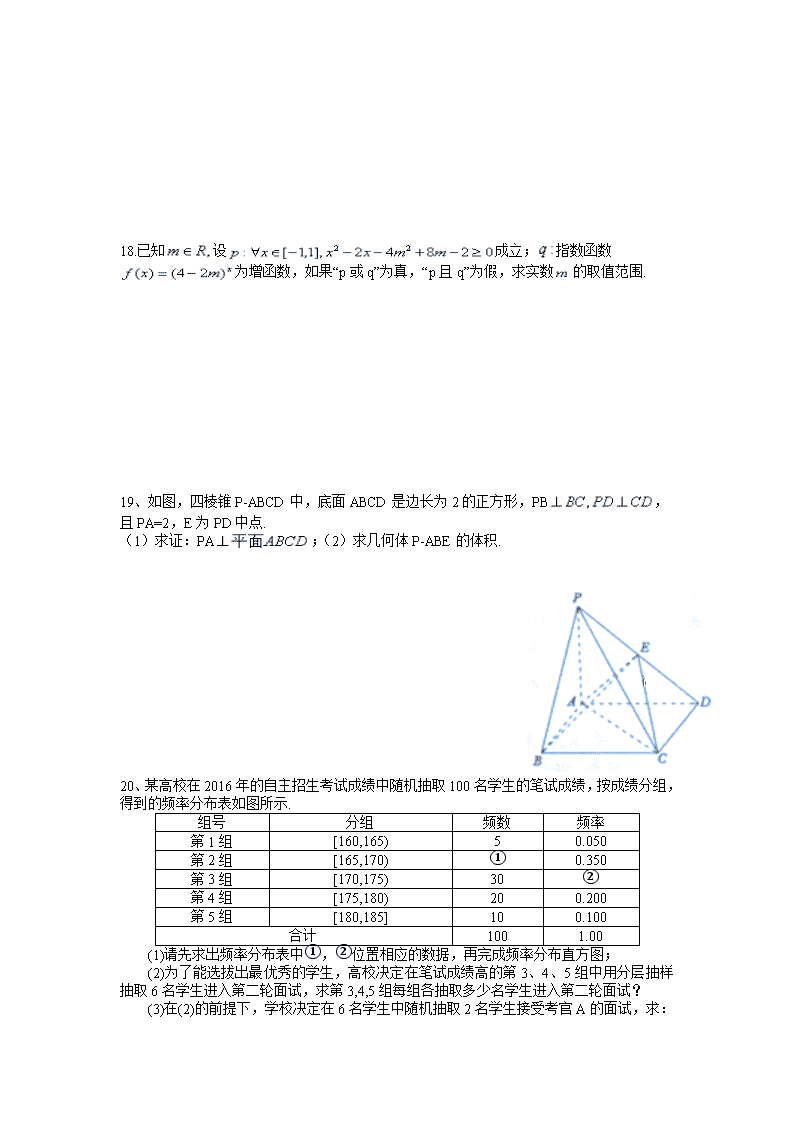20、某高校在2016年的自主招生考试成绩中随机抽取100名学生的笔试成绩，按成绩分组，得到的频率分布表如图所示.‎ 组号 分组 频数 频率 第1组 ‎[160,165)‎ ‎5‎ ‎0.050‎ 第2组 ‎[165,170)‎ ‎①‎ ‎0.350‎ 第3组 ‎[170,175)‎ ‎30‎ ‎②‎ 第4组 ‎[175,180)‎ ‎20‎ ‎0.200‎ 第5组 ‎[180,185]‎ ‎10‎ ‎0.100‎ 合计 ‎100‎ ‎1.00‎ ‎(1)请先求出频率分布表中①，②位置相应的数据，再完成频率分布直方图；‎ ‎(2)为了能选拔出最优秀的学生，高校决定在笔试成绩高的第3、4、5组中用分层抽样抽取6名学生进入第二轮面试，求第3,4,5组每组各抽取多少名学生进入第二轮面试？‎ ‎(3)在(2)的前提下，学校决定在6名学生中随机抽取2名学生接受考官A的面试，求：第4组至少有一名学生被考官A面试的概率．‎ ‎21．已知长方体ABCD-A1B1C1D1中，底面ABCD为正方形，AB=4，AA1=2，点E1在棱C1D1上，且D1E1=3。‎ ‎（I）在棱CD上确定一点E，使得直线EE1∥平面D1DB，并写出证明过程；‎ ‎（II）若动点F在正方形ABCD内，且AF=2，请说明点F的轨迹，试求E1F长度的最小值。‎ ‎22．已知圆O：和定点A(2,1)，由圆O外一点向圆O引切线PQ，切点为Q，且满足．‎ ‎(1) 求实数a、b间满足的等量关系；‎ ‎(2) 求线段PQ长的最小值；‎ ‎(3) 若以P为圆心所作的圆P与圆O有公共点，试求半径取最小值时圆P的方程．‎